Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Метод параллельного переноса
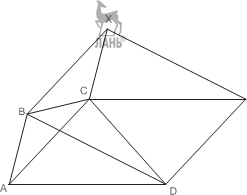
В этом разделе будут рассмотрены задачи, решаемые с помощью параллельного переноса. В таких задачах часть фигуры переносят параллельно самой себе так, чтобы новую фигуру было легче построить, чем искомую. После построения новой фигуры надо сделать обратный параллельный пере- нос, чтобы вернуться к исходной задаче. Многие задачи на построение четырёхугольников можно решить с помощью построения вспомогательного параллелограмма, стороны которого параллельны и равны диагоналям искомого четырёхугольника. Рассмотрим четырёхугольник ABCD. Перенесем диагональ AC параллельно самой себе в отрезки BX и DY. Полученный параллелограмм BXY D будет обладать следующими свойствами.
1)
2) Расстояния от точки C до вершин параллелограмма BXY D равны сторонам исходного четырёхугольника. 3) Углы между отрезками, соединяющими точку C с вершинами параллелограмма BXY D, равны углам исходного четырёхугольника. 4) Площадь параллелограмма вдвое больше площади четырёхугольника. 5) Диагонали параллелограмма вдвое больше отрезков, соединяющих середины сторон AB и CD, BC и AD; угол между диагоналями равен углу между этими отрезками. 6) Углы ∠ XCD и ∠ BCY дополняют углы между противоположными сторонами AB и CD, BC и AD до 180◦. Докажем эти свойства. 1) Стороны параллелограмма параллельны и равны диагоналям четырёхугольни- ка, следовательно, угол параллелограмма равен углу между этими диагоналями. 2) Отрезки BC и CD являются сторонами четырёхугольника. Отрезки CX и CY параллельны и равны сторонам AB и AD, поскольку ABXC и ACY D – параллелограммы. 3) Углы ∠ BCX = ∠ ABC и ∠ DCY = ∠ CDA как внутренние накрест лежащие при параллельных прямых. Углы ∠ XCY = ∠ BAD как углы с параллельными сторонами. 4) Обозначим диагонали ABCD через d 1, d 2 и угол между ними через α. Тогда
1
откуда S BXY D = 2 S ABCD. 5)
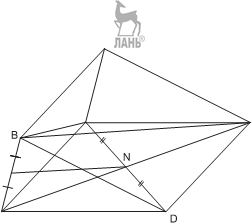 Пусть отрезок MN соединяет середины сторон AB и CD. Пусть отрезок MN соединяет середины сторон AB и CD.
Так как диагонали параллелограмма точкой пересечения делятся пополам, то N есть точка пересечения диагоналей параллелограмма ACY D, а отрезок MN есть средняя линия Δ ABY.
Следовательно, MN = BY/ 2, что и требовалось доказать. 6)
З а м е ч а н и е. В случае, когда стороны BC и AD параллельны (то есть ABCD трапеция), ломаная BCY выпрямляется.
Примеры решения задач П р и м е р 1. Построить четырёхугольник, зная его углы и две противоположные стороны.
можем. Точку C можно получить как точку пе- ресечения луча, отложенного от прямой AD под углом δ, и луча, отложенного от прямой AE под углом β. Затем, переместив отрезок
П р и м е р 2. Построить отрезок, равный и параллельный данному так, чтобы один конец лежал на данной прямой, другой – на данной окружности.
Р е ш е н и е. Пусть даны прямая m, отрезок AB и окружность.
Задача может иметь одно решение, два решения или не иметь решений вообще.
П р и м е р 3. Построить трапецию по двум диагоналям и двум основаниям. Р е ш е н и е. Рассмотрим трапецию ABCD с диагоналями AC и BD. Перенесём диагональ BD вдоль основания BC. Получим параллелограмм BCED.
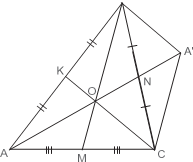
П р и м е р 4. Построить треугольник по трём его медианам. Р е ш е н и е. Пусть медианы BM = m b, AN = m a и CK = m c треугольника ABC пересекаются в точке O. Перенесём отрезок BO параллельно самому себе в отрезок A C.
Так как медианы в треугольнике точкой пересечения делятся в отношении
OB = , BA = OC = 2 m.
3 c
Кроме того, поскольку в параллелограмме диагонали точкой пересечения де- лятся пополам, OA = 2 ON = 2 m.
3 a Таким образом, треугольник OBA мы можем построить по трём сторонам. Затем, достроив его до параллелограмма OBA C, получим вершину C. Далее, отложив отрезок AO = OA , получим вершину A.
П р и м е р 5. Построить четырёхугольник, зная две диагонали, угол между ними и две противолежащие стороны.
Р е ш е н и е. Зная две диагонали и угол между ними, мы можем построить вспо- могательный параллелограмм BXY D. Согласно свойству 2 (сформулированному в теоретической части) отрезки BC и CY равны противолежащим сторонам че- тырёхугольника и точку C мы можем найти как точку пересечения дуг соответ- ствующих радиусов. Достроив Δ CY D до параллелограмма, получим вершину A.
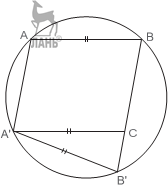
П р и м е р 6. Через две точки, данные на окружности, провести две параллель- ные хорды, разность которых равна данной величине.
Треугольник, равный треугольнику Δ A B C, можно построить по трём сто- ронам. После этого надо отложить от AB угол, равный углу ∠ A CB. Так мы найдем точку B. Точку A можно получить как точку пересечения прямой, па- раллельной BB, с окружностью. З а м е ч а н и е. Если в условии задачи дана сумма (разность) отрезков или углов, надо так преобразовать исходную фигуру, чтобы эта величина входила в преобра- зованную фигуру.
Задачи 1. Построить трапецию по четырём сторонам.
2.
3. Построить треугольник, зная m a, m c, ∠(m b, a). 4. Через точку A внутри угла провести прямую так, чтобы отрезок, заключён- ный между сторонами, делился точкой A пополам.
5. Построить трапецию, зная диагонали, угол между ними и одну из боковых сторон.
6. Построить четырёхугольник, зная две диагонали, две противолежащие сто- роны и угол между ними.
7. Через данную точку M провести прямую так, чтобы разность расстояний до неё от двух данных точек A и B была равна данной длине.
1 Имеется в виду, что один конец отрезка лежит на одной окружности, второй – на другой.
8. В данный остроугольный треугольник вписать прямоугольник с наименьшей диагональю (одна сторона прямоугольника лежит на основании треуголь- ника).
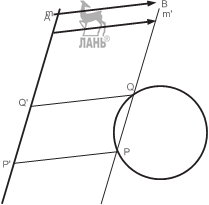
9. Даны три параллельные прямые. Провести через данную точку секущую так, чтобы разность отрезков между параллелями была равна заданной величине.
10. Построить трапецию ABCD, зная боковую сторону CD, угол между диаго- налями, расстояние между параллельными сторонами и отрезок, соединяю- щий середины боковых сторон.
11. Построить треугольник по b, c и m a.
12. Построить четырёхугольник, зная его стороны и отрезок, соединяющий се- редины двух противоположных сторон.
13.
14. Построить биссектрису угла, вершина которого недоступна.
15. Даны две точки A и B и между ними две параллели m и n. Провести между этими параллелями в данном направлении отрезок CD так, чтобы сумма AC + CD + BD была минимальной.
16. На окружности даны две точки A и B. В данном направлении провести хорду XY так, чтобы сумма хорд AX и BY была равна заданной величине.
17. Построить прямоугольник с данной стороной так, чтобы его стороны прохо- дили через четыре заданные точки.
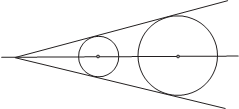
18. Даны две окружности и прямая. Провести параллельно этой прямой секу- щую, отсекающую в окружностях хорды, сумма которых равна заданному отрезку длины s.
Метод подобия Теоретический материал
Если два подобных многоугольника расположены так, что их соответствующие стороны параллельны, то прямые, соединяющие вершины равных углов, пересека- ются в одной точке. Эта точка называется центром гомотетии или центром по- добия, а многоугольники называются гомотетическими. Отношение расстояний от центра подобия до соответствующих вершин гомотетических многоугольников равно коэффициенту их подобия. Центр подобия может лежать внутри многоугольников, может – вне, может совпадать с одной из вершин или принадлежать одной из сторон.
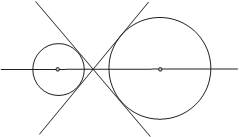
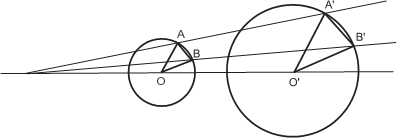
Центром подобия двух окружностей называется точка пересечения их общих внешних касательных. Центр подобия лежит на линии центров окружностей. От- ношение расстояний от центра подобия до центров окружностей равно отношению радиусов. Точка пересечения внутренних касательных к двум окружностям называется обратным центром подобия, который обладает аналогичными свойствами.
Метод подобия заключается в том, что сначала мы строим фигуру, ещё не удовлетворяющую всем условия задачи, но подобную искомой фигуре. Потом, ис- пользуя остальные условия, преобразуем построенную фигуру в искомую. 5.5.
Примеры решения задач П р и м е р 1. Построить треугольник по двум углам и биссектрисе третьего угла.
Проведём в нём биссектрису CL и отложим на ней отрезок CL = l c. Через точку L проведём прямую, параллельную A B. Углы и биссектриса полученного треугольника Δ ABC равны заданным.
П р и м е р 2. Построить треугольник по α, β и a + h a. Р е ш е н и е. Построим Δ AB C по двум углам α, β и высоте h a = a + h a, про- ведённой к стороне B C = a. Искомый треугольник ABC подобен треугольнику AB C и
Следовательно, h a = h 2
a + h a янии h a от точки A и через точку H проведём прямую, параллельную пря- мой B C . Построенный треугольник ABC удовлетворяет заданным условиям.
П р и м е р 3. Построить треугольник по трём высотам h a, h b, h c.
p 2 p 2
h a h b p 2
2 S 2 S Пусть S – площадь искомого треугольника, тогда его стороны a =
h c , b = ,
Для того чтобы построить искомый треугольник A BC с высотами h a, h b, h c, достаточно в треугольнике A B C на прямой A H отложить отрезок A H = h a и через точку H провести прямую BC, параллельную B C . Задача имеет решение, если существует треугольник, построенный из отрезков 1 1 1
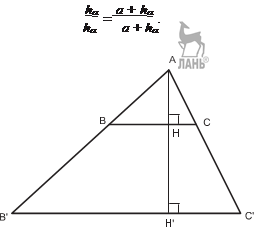
Р е ш е н и е. Построим прямоугольный треугольник A B C с катет√а м и A B = a, BC = 2 a, где a – произвольный отрезок. Тогда гипотенуза AC = a 5.
пендикуляр DH. Из подобия треугольников DHC и ABC получаем следовательно, CH = 2. CH DC
BC AC
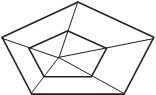
Р е ш е н и е. Пусть точка O – центр заданно- го сектора. Построим вспомогательный квадрат ABCD, две вершины которого (A и D) лежат на радиусах сектора на равном расстоянии от точки O. Проведём прямые OB и OC, они пересекут дугу сектора в точках B и C.
Задачи 1. Построить треугольник по двум углам и высоте, проведенной из третьего угла. 2. Построить окружность, касающуюся сторон данного угла и проходящую че- рез заданную внутри него точку.
3.
4.
5. Построить треугольник по α, β, r. 6. Через данную точку провести прямую, отсекающую от двух данных окруж- ностей хорды, пропорциональные их радиусам. 7. Дан угол ABC и точка M внутри него. Найти на стороне BC точку X, равноудалённую от AB и точки M. 8. Даны три точки A, B и C, не лежащие на одной прямой. Провести пря- мую, пересекающую отрезок AC в точке X, а отрезок BC в точке Y таким образом, что AX = XY = Y B. 9. Даны две окружности и на них по точке. Провести две равные окружности, касающиеся друг друга и двух данных окружностей в заданных точках. 10. Через данную точку A провести к двум данным окружностям секущую, отсекающую в окружностях а) равные хорды; б) хорды, длины которых находятся в заданном соотношении. 11. Построить треугольник, зная β, l b и AD: DC, где BD – высота.
12. Даны три концентрические окружности. Провести секущую ABC так, чтобы точки A, B и C лежали на разных окружностях и AB = BC. 13. Через две точки, лежащие вне данной окружности, провести окружность, касающуюся заданной окружности. 14. Даны две окружности с центрами в точках O и O. Через центр их подо- бия S проведены касательная и секущая. Касательная касается окружностей в точках C и C соответственно, секущая отсекает от окружностей хорды AB и A B. Доказать, что CS · C S = AS · B S = BS · A S. 15.
5.6. Метод поворота и смешанные задачи Теоретический материал В этом разделе рассматриваются задачи, решаемые с помощью поворота фигу- ры (или её части) относительно некоторой неподвижной точки плоскости (центра поворота). Также приводятся задачи, не попадающие однозначно ни под один из предло- женных ранее типов задач, и задачи, решение которых требует комбинирования нескольких методов.
Примеры решения задач
З а меч а ни е. Если точки B и B совпадают, то задача имеет одно решение. Если постро- енная окружность не пересекает окружность с центром в точке O, то решений нет.
П р и м е р 2. Даны две окружности, треугольник и точка A. Построить тре- угольник ABC, подобный данному, так, чтобы вершины B и C лежали на окруж- ностях.
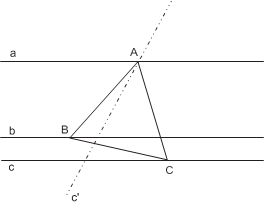
П р и м е р 3. Построить равносторонний треугольник, вершины которого лежат на трёх данных параллельных прямых. Ре ш е н и е. Пусть a, b, c – три данные параллельные прямые.
∠ B = 60◦.
П р и м е р 4. В треугольнике найти точку, сумма расстояний от которой до вер- шин минимальна. Р е ш е н и е. Рассмотрим произвольную точку P внутри треугольника ABC. Повернем Δ ABP относительно точки A на 60◦, получим Δ AB P . При этом B P = BP и PP = AP (так как Δ AP P равносторонний), следовательно, BP + AP + CP = B P + P P + PC,
Следовательно, для построения искомой точки P надо сначала построить точ- ку B (повернуть отрезок AB относительно A на 60◦). Точки P и P должны быть расположены на отрезке B C таким образом, чтобы треугольник AP P был равносторонним, поэтому они должны лежать на лучах, отложенных от перпен- дикуляра AH под углом 30◦.
П р и м е р 5. Построить треугольник по заданным отрезкам медианы, биссек- трисы и высоты, проведённым из одной вершины. Р е ш е н и е. Рассмотрим треугольник ABC с данными высотой BH, биссектри- сой BL и медианой BM. Продолжим биссектрису BL до пересечения с описанной окружностью в точке B (так как ∠ ABB = ∠ CBB , то B – середина дуги AC). Теперь через точку M проведём перпендикуляр к хорде AC. Точка B (сере- дина дуги) и точка O (центр описанной окружности) принадлежат этому сере- динному перпендикуляру.
Центр окружности O есть точка пере- сечения прямой MB и серединного пер- пендикуляра к хорде BB. Вершины A и C есть точки пересечения этой окружно- сти с прямой HM. Задачи 1.
2. Даны прямая и окружность. Построить окружность, касающуюся данной окружности и прямой в данной точке. 3. Даны две окружности. Провести к ним через заданную точку две секущие, пересекающиеся под заданным углом и отсекающие а) равные хорды; б) хорды, длины которых находятся в заданном отношении. 4. В данный параллелограмм ABCD вписать равнобедренный треугольник AP Q (AP = AQ) с данным углом при вершине A. 5. Построить четырёхугольник, вписываемый в окружность, зная его стороны a, b, c и d. 6. Провести через заданную точку прямую, отсекающую от данной окружности хорду заданной длины. 7.
8. Провести через точку B пересечения двух окружностей прямую, высекаю- щую из окружностей равные хорды. 9. Через точку A внутри угла провести прямую, отсекающую от угла треуголь- ник минимального периметра. 10. Даны три точки. Построить окружности, попарно касающиеся в этих точках. 11. Построить треугольник, зная a, h a и ∠(m b, c). 12. Через вершину выпуклого четырёхугольника провести прямую, которая де- лит его площадь пополам.
Стереометрия Введение в стереометрию Приведём основные стереометрические определения, связанные с взаимным рас- положением прямых и плоскостей в пространстве.
Параллельность прямых и плоскостей в пространстве Две прямые в пространстве называются параллельными, если они лежат в одной плоскости и не пересекаются. Прямая и плоскость называются параллельными, если они не пересекаются.
Скрещивающиеся прямые Прямые, которые не лежат в одной плоскости и не пересекаются, называются скрещивающимися. Угол между скрещивающимися прямыми определяется как угол между па- раллельными им прямыми, проходящими через одну точку. Общим перпендикуляром двух скрещивающихся прямых называется отрезок, концы которого лежат на этих прямых, перпендикулярный к ним (такой отрезок существует и притом только один).
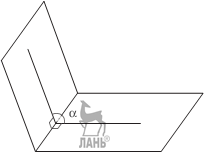
Двугранным углом называется фигура, образованная двумя полуплоскостями (гранями) с общей ограничивающей их прямой (ребром двугранного угла). Двугранный угол измеряется своим линейным углом, то есть углом между перпендикулярами к ребру, восстановленными в обеих плоскостях из одной точки.
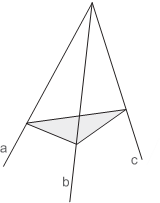
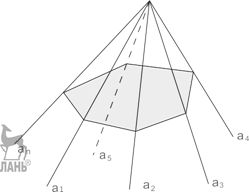
Многогранный угол Трехгранным углом (abc) называется фигура, составленная из трех плоских углов (ab), (bc) и (ac), не лежащих в одной плоскости. Эти углы называются гранями трехгранного угла, а их стороны – ребрами. Общая вершина плоских углов называется вершиной трехгранного угла. Двугранные углы, образованные гранями трехгранного угла, называются двугранными углами трехгранного угла. Аналогичным образом определяется понятие n-гранного угла (a 1 a 2 ...a n) – как фигуры, составленной из n плоских углов (a 1 a 2), (a 3 a 3), ..., (a n a 1).
Многогранный угол называется выпуклым, если он лежит по одну сторону каждой из ограничивающих его плоскостей.
З а м е ч а н и е 1. Каждый плоский угол трехгранного угла меньше суммы двух других плоских углов. З а м е ч а н и е 2. Сечением выпуклого n -гранного угла плоскостью, не проходя- щей через вершину, является выпуклый n -угольник. З а м е ч а н и е 3. В выпуклом многогранном угле сумма плоских углов не пре- восходит 360◦.
Перпендикулярность прямых и плоскостей в пространстве
Две плоскости перпендикулярны, если соответствующий двугранный угол яв- ляется прямым.
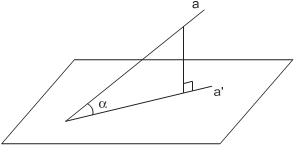
Наклонная Наклонной, проведенной к данной плоскости, называется прямая, пересекаю- щая плоскость, но не перпендикулярная ей. Точка пересечения наклонной и плос- кости называется основанием наклонной. Проекцией точки на плоскость называется основание перпендикуляра, опу- щенного из данной точки на данную плоскость.
Проекцией наклонной на плоскость называется прямая, состоящая из проекций всех точек наклонной на данную плоскость. Углом между наклонной и плоскостью называется угол между наклонной и её проекцией.
Теоремы о параллельности прямых и плоскостей
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-01-14; просмотров: 1081; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.226.248 (0.287 с.) |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||




 S ABCD = 2 d 1 d 2 sin α, S BXY D = d 1 d 2 sin α,
S ABCD = 2 d 1 d 2 sin α, S BXY D = d 1 d 2 sin α,


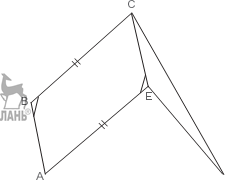 Р е ш е н и е. Пусть в четырёхугольнике ABCD даны углы α, β, γ, δ и стороны BC и AD. Перенесём BC параллельно самой себе в AE.
Р е ш е н и е. Пусть в четырёхугольнике ABCD даны углы α, β, γ, δ и стороны BC и AD. Перенесём BC параллельно самой себе в AE.


 2: 1, то в параллелограмме OBA C стороны
2: 1, то в параллелограмме OBA C стороны






 Метод подобия 157
Метод подобия 157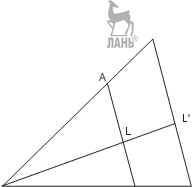 Ре ше н и е. Пусть даны углы α, β и отрезок l c. Построим произвольный тре- угольник Δ A B C с двумя данными углами.
Ре ше н и е. Пусть даны углы α, β и отрезок l c. Построим произвольный тре- угольник Δ A B C с двумя данными углами.
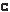




 a = , b =
a = , b = и c = . h c
и c = . h c c = 2 S. Следовательно, искомый треугольник и Δ A B C подобны.
c = 2 S. Следовательно, искомый треугольник и Δ A B C подобны.




 П р и м е р 4. Дан отрезок длины √5. С помощью циркуля и линейки построить отрезок длины 2.
П р и м е р 4. Дан отрезок длины √5. С помощью циркуля и линейки построить отрезок длины 2.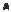
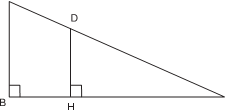


 = ,
= ,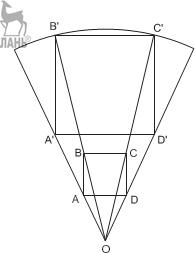 П р и м е р 5. В круговой сектор вписать квадрат.
П р и м е р 5. В круговой сектор вписать квадрат.

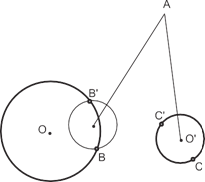
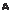
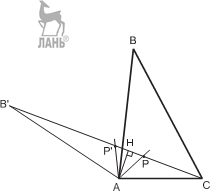 то есть сумма расстояний от точки P до вершин треугольника равна длине ло- маной B P PC ≥ B C. Минимальное значение длины ломаной равно B C при P, P ∈ B C.
то есть сумма расстояний от точки P до вершин треугольника равна длине ло- маной B P PC ≥ B C. Минимальное значение длины ломаной равно B C при P, P ∈ B C.

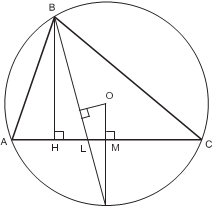 Таким образом, для того чтобы постро- ить Δ ABC, сначала надо построить тре- угольник BHM (по заданным гипотенузе BM и катету BH), потом на отрезке MH отметить точку L (биссектриса всегда ле- жит между медианой и высотой) и найти точку B как точку пересечения перпен- дикуляра к прямой HM в точке M и пря- мой BL.
Таким образом, для того чтобы постро- ить Δ ABC, сначала надо построить тре- угольник BHM (по заданным гипотенузе BM и катету BH), потом на отрезке MH отметить точку L (биссектриса всегда ле- жит между медианой и высотой) и найти точку B как точку пересечения перпен- дикуляра к прямой HM в точке M и пря- мой BL.

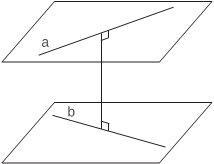 Расстоянием между двумя скрещивающимися прямыми называется длина их общего перпендикуляра (оно же является и расстоянием между параллельными плоскостями, содержащими эти прямые).
Расстоянием между двумя скрещивающимися прямыми называется длина их общего перпендикуляра (оно же является и расстоянием между параллельными плоскостями, содержащими эти прямые).
 Двугранный угол
Двугранный угол