Метод симметрии и спрямления

Теоретический материал

В случаях, когда нужную фигуру сразу построить затруднительно, бывает удобно преобразовать её в другую фигуру, которую построить легче.

В этом разделе будут рассмотрены задачи, решаемые с помощью преобразова- ния фигур методом симметрии и спрямления.

⊥

Точки A и B называются симметричными относительно прямой m, если отрезок AB m и делится этой прямой пополам. Прямую m называют осью симметрии. Точку B называют отражением точки A и наоборот.

 

Фигуры, все точки которых являются симметричными относительно пря- мой m, называются симметричными относительно этой прямой.

 

Метод симметрии заключается в следующем. Считаем, что нужная фигура по- строена, и отражаем часть фигуры (точку, прямую, окружность) относительно некоторой оси. Изменённую фигуру подчиняем тем же условиям, которым должна удовлетворять исходная фигура, и решаем новую задачу уже известными спосо- бами.

В ряде задач метод симметрии приводит к спрямлению ломаных линий в пря- мые. Метод спрямления состоит в следующем. Считаем задачу решённой и в полученном чертеже некоторую ломаную линию заменяем прямой. Таким обра- зом исходная задача заменяется новой – более простой. После построения новой фигуры определяется, в какой точке надо согнуть выпрямленную линию, чтобы вернуться к исходной задаче.

Метод спрямления особенно часто применим в задачах, где дана сумма или разность частей некоторой ломаной линии.

146                                                                                          Теория и задачи

Примеры решения задач

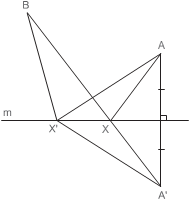
П р и м е р 1. Дана прямая m и две точки A и B по одну сторону от неё. Найти на прямой m точку X такую, что сумма расстояний AX и BX минимальна.

Р е ш е н и е. Рассмотрим точку A, симметричную точке A относительно пря- мой m. Обозначим через X точку пересечения отрезка A B с прямой m. Имеем

AX + XB = A X + XB = A B.

Для любой другой точки X ∈ m будет выполняться

AX + X B = A X + X B > A B.

Следовательно, искомая точка X – это точка пересечения отрезка A B с пря- мой m.

 

П р и м е р 2. Построить треугольник по периметру P и двум углам α и β.

Р е ш е н и е. Пусть треугольник ABC с данными ∠ A = α, ∠ C = β, P _ABC = P

уже построен. На прямой AB отложим отрезки AA = AC и BB = BC.

 

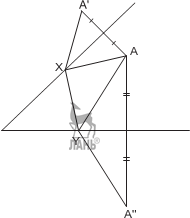
Треугольники AA C и BB C равнобедренные с углами при основании соот-

α

ветственно

2

и β. Следовательно, у треугольника A B C сторона A B = P и

2

∠ A = α, ∠ B = β.

2              2

Таким образом, для того чтобы построить Δ ABC, сначала нам надо построить

Δ A B C по стороне и двум прилежащим углам, потом провести к сторонам A C

и B C серединные перпендикуляры, которые пересекут A B соответственно в точках A и B.

Построенный треугольник ABC будет удовлетворять заданным условиям, то есть P _ABC = P и ∠ BAC = α, ∠ BCA = β.

П р и м е р 3. Даны отрезок AB и прямая, пересекающая его. Построить тре- угольник ABC, биссектриса которого принадлежит данной прямой.

Р е ш е н и е. Построим отражение точки A относительно прямой m. Проведём через B и полученную точку A прямую, которая пересечёт исходную прямую m в точке C.

Пусть H – точка пересечения отрезка AA с прямой m. Прямоугольные треуголь- ники Δ ACH и Δ A CH равны друг другу и, следовательно, ∠ ACM = ∠ BCM.

 

П р и м е р 4. Внутри угла дана точка A. Найти такое положение точек X и Y

на сторонах угла, чтобы периметр треугольника AXY был минимальным.

Ре ш е н и е. Пусть A и A – отражения точки A относительно сторон угла. Длина ломаной A XY A равна периметру Δ AXY.

 

Так как ломаная имеет минимальную длину в случае, когда является отрезком, то искомые точки X, Y – это точки пересечения отрезка A A со сторонами угла.

 

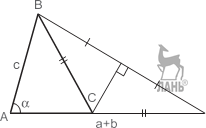
П р и м е р 5. Построить треугольник, зная α, c и a + b.

Ре ше ни е. От отрезка AD = a + b отложим под углом α отрезок AB = c. В качестве вершины C возьмём точку пересечения серединного перпендикуляра к отрезку BD с отрезком AD.

 

Так как отрезки BC и DC равны между собой, построенный треугольник

Δ ABC удовлетворяет всем данным в условии задачи требованиям.

 

Задачи

1. Построить треугольник, зная P, α и h _a.

2. Даны две окружности и между ними прямая. Начертить равносторонний треугольник так, чтобы две его вершины были на окружностях, а одна из высот лежала на данной прямой.

3. Дана прямая m и две точки A и B по одну сторону от неё. Найти на m

такую точку X, чтобы AX составлял с m угол, вдвое больший, чем BX.

4. Внутри угла даны точки A и B. Построить равнобедренный треугольник, основание которого лежит на одной стороне угла, вершина – на другой, а боковые стороны проходят через точки A и B.

5. Дана прямая AB и две окружности, лежащие по одну сторону от прямой. Найти на прямой AB точку, касательные из которой составляют с этой пря- мой равные углы.

6.

∈        ∈

Точки A и B расположены между параллельными прямыми m и n. По- стройте точки M m, N n так, чтобы длина ломаной AM NB была наименьшей.

7. В данную окружность вписать прямоугольник, зная разность основания и высоты.

8. Построить треугольник по стороне, прилежащему углу и разности остальных сторон.

9. Построить четырёхугольник ABCD, зная его стороны, если диагональ AC

делит угол A пополам.

10. Найти сумму перпендикуляров, опущенных на стороны равнобедренного тре- угольника из точки, взятой на основании.

 

11. Найти сумму перпендикуляров, опущенных из точки, взятой внутри равно- стороннего треугольника, на его стороны.

12. На окружности даны точки A и B. Отыскать на ней точку X такую, что

AX + BX = a, где a – заданный отрезок.

13. На окружности даны точки A и B. Отыскать на ней точку X такую, что

AX − BX = a, где a – заданный отрезок.

14. Найти геометрическое место точек, сумма расстояний от которых до двух данных пересекающихся прямых равна заданному отрезку.

15. На данной прямой найти такую точку, что разность расстояний от неё до сторон данного угла равна данному отрезку.

16. Провести окружность, касающуюся двух данных окружностей, так, чтобы радиусы, проведённые из центра искомой окружности к точкам касания, об- разовывали данный угол.

17. Построить равнобедренный треугольник, зная его боковую сторону a и сум- му высоты с основанием s.

18. Построить треугольник по a, m _b + b и ∠(m _b, b).

19. Построить треугольник по b, c и β − γ.