Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Відношення порядку на множині цілих невідємних чисел. Дискретність на множині цілих невідємних чисел. Поняття про скінченну множину.
Відношення «безпосередньо слідує за» зв’язує не будь – які невідємні числа, а лише сусідні числа а і а′. Тому виникає проблема розширення цього зв’язку до відношення порядку на множині цілих чисел. Кажуть, що ціле невідємне число а більше за число в і позначають ав, якщо існує таке натуральне число, що а=в+k. При цьому говорять також, що в менше від а і позначають ва. Множина цілих невідємних чисел упорядкована відношенням «більше», тобто: 1) для будь – яких її чисел а і в виконується одне і тільки одне з трьох відношень а=в; ав; ав. 2) кожне з цих відношень транзитивне, наприклад, якщо ав всас. Оскільки за теоремою для а і в виконується одне і тільки одне із співвідношень а=в; а>в; а<в, то зрозуміло,що ав=ва. Таким чином, відношення «більше» є асиметричним і транзитивним, тобто відношенням строгого порядку на множині цілих невідємних чисел. Множину натуральних чисел, упорядковану за відношенням «безпосередньо йде за», або відношенням «менше», називають натуральним рядом чисел. Множину N₀ називають розширенням натурального ряду, N₀=N{0}. Множина N₀ задовольняє принцип найменшого числа: будь – яка сукупність її чисел має єдине найменше число. За кожним числом у множині N₀ безпосередньо йде єдине число і кожне ціле невідємне число, крім нуля, безпосередньо йде не більше, ніж за одним цілим невідємним числом. Отже, для кожної пари чисел а і а′ не можна вказати ніякого третього числа х такого, що аха′. Тобто дискретність на множині цілих невідємних чисел означає, що між елементом а та безпосередньо наступним елементом а′ немає жодного елемента цієї множини. Множина називається скінченною, якщо вона не рівнопотужна жодній своїй власній підмножині.(кількісна теорія). Скінченна множина – це множина рівнопотужна деякому відрізку натурального ряду чисел.
20. Поняття про натуральне число, як спільну властивість класу скінчених рівнопотужних множин. Поняття про нуль. Відношення рівності на множині цілих невід’ємних чисел, відношення „менше” („більше”)на множині цілих невід’ємних чисел, їх властивості.
21. Означення суми двох цілих невід’ємних чисел. Існування суми, її єдність. Операція додавання на множині цілих невід’ємних чисел. Закони додавання: комутативний, асоціативний. Поняття суми і додавання в початковому курсі математики.
За властивостями скінченних множин об'єднання двох скінченних множин є скінченною множиною, а тому сума довільних двох цілих невід'ємних чисел є цілим невід'ємним числом. Оскільки об'єднання множин завжди існує і визначається однозначно, то й сума двох довільних цілих невід'ємних чисел завжди існує і визначається однозначно. Отже, доведено теорему. Теорема. Сума двох довільних цілих невід'ємних чисел є цілим невід'ємним числом. Вона завжди існує і визначається однозначно.
Означення різниці двох цілих невід’ємних чисел. Умови існування різниці, її єдиність. Операція віднімання на множині цілих невід’ємних чисел. Зв’язок віднімання з додаванням. Поняття різниці і віднімання в початковому курсі математики. 1.Різницею цілих невід’ємних чисел a і b називається число с, яке є потужністю доповнення підмножини В до множини А: а – b = c N(A) – N(B) = N(B᷃A) Число а називають зменшуваним, b – від’ємником, с – різницею, а операцію знаходження різниці – дією віднімання. 2. Теорема 10. Для довільних цілих невід'ємних чисел a та b їх різниця існує тоді і тільки тоді, коли a ≥ b. Якщо різниця цілих невід'ємних чисел існує, то вона єдина.
► І. Доведемо існування різниці. 1) Нехай a ≥ b. Можливі два випадки або a = b, або a > b. Якщо a = b, то за властивістю нуля при додаванні будемо мати b + 0 = a. Звідси за означенням різниці одержуємо a – b = 0. Якщо ж a > b, то за означенням відношення "більше" дістанемо b x = a, де x N. Звідси за означенням різниці a – b = x. 2) Нехай різниця цілих невід'ємних чисел a та b існує. Покажемо, що a ≥ b. Дійсно, оскільки різниця цілих невід'ємних чисел a і b існує, то за означенням різниці знайдеться ціле невід'ємне число x таке, що b + x = a. Для x можливі два випадки: або x = 0, або x ≠ 0 (тобто, x N). Якщо x = 0, то з того, що b + 0 = a, випливає (за властивістю нуля при додаванні) b = a. Якщо ж x N, то з того, що b + x = a, одержуємо (за означенням відношення "більше") a > b. А тому маємо, що при існуванні різниці чисел a і b, a ≥ b. Отже, існування різниці доведено. ІІ. Доведемо єдиність різниці. Нехай різниця цілих невід'ємних чисел a і b існує. Припустимо, що a − b = x 1, і a – b = x 2. Звідси за означенням різниці маємо a = b + x 1 і a = b + x 2. Отже, b + x 1 = b + x 2 і за правилом скорочення для додавання одержимо x 1 = x 2. Значить, різниця цілих невід'ємних чисел, якщо вона існує, визначається однозначно. ◄ З доведеної теореми одержуємо наслідок. Наслідок 5. a 0: a – 0 = a; a 0: a – a = 0. 3. Операція у множині цілих невід'ємних чисел, при якій кожній парі чисел a і b ставиться у відповідність їх різниця a – b, називається відніманням цілих невід'ємних чисел. Компоненти віднімання називаються: перша – зменшуваним, друга – від'ємником, а результат – різницею. 4. На підставі означення різниці через суму одержуємо, що віднімання цілих невід'ємних чисел є оберненою операцією до додавання. А теорема 10 показує, що віднімання є частковою операцією для цілих невід'ємних чисел. Оскільки А = В ∪ B᷃A і В ⋂ B᷃A = ∅, за означенням суми цілих невід’ємних чисел N(A) = N(B) + N(B᷃A), тобто a = b + c. Отже віднімання – дія обернена до дії додавання. 5. У шкільній математиці віднімання вводиться на основі практичних вправ, пов'язаних з виділенням підмножини даної множини і утворення нової множини – доповнення виділеної підмножини. При цьому, звичайно, теоретико-множинна символіка і термінологія не використовуються, а число елементів підмножини і її доповнення знаходяться способом переліку. Головним засобом розкриття теоретико-множинного смислу віднімання є розв'язування простих задач.
Зв'язок віднімання з додаванням встановлюється при розгляді теми "як знайти невідомий доданок". Означення віднімання, як операції оберненої до додавання, в явному виді не дається, але постійно використовується. Правила віднімання числа від суми і суми від числа вводяться ще у першому класі, по суті, на теоретико-множинній основі. Приклади, які розглядаються при цьому, ілюструються наочністю.
Означення добутку двох цілих невід’ємних чисел. Існування добутку, його єдиність. Операція множення на множині цілих невід’ємних чисел. Закони множення: комутативний, асоціативний, дистрибутивний відносно додавання. Поняття добутку і множення в початковому курсі математики. 1.Добуток цілих невід’ємних чисел позначається через декартовий добуток множин та через суму однакових доданків. Означення 1. Добутком цілих невід’ємних чисел m і k називається число елементів декартового добутку множини що має m елементів на множину що має k елементів. Означення 2. Добутком цілого невід’ємного числа m на натуральнее число k називається сума k доданків кожен з яких дорівнює m m*k = m+m+….+m } k Числа m і k називають множниками, а операцію знаходження добутку – дію множення. Добуток цілого невід’ємного числа числа а на 1 є число а: (∀а є N0) а *1=а Добуток цілого невід’ємного числа а на 0 є нуль: (∀а є N0) а*0=0 2. Теорема 6. (про існування та єдиність добутку): якими б не були цілі невід’ємні числа a і b завжди існує єдине ціле невід’ємне число a×b, яке є їх добутком. Доведення: Для доведення теореми використаємо означення добутку через суму однакових доданків, розглянувши три випадки: 1) b=0; 2) b=1; 3) b>1. Якщо b=0, то добуток а×0 існує згідно з додатковим означенням: а×0=0. Якщо b=1, то добуток а×1 також існує згідно з додатковим означенням: а×1=а. В обох випадках добутки єдині. Якщо b>1, то добуток існує і єдиний, бо існує і єдина сума а+а+а+...+а=а×b. Теорему доведено. 3. Поняття добутку двох цілих невід'ємних чисел можна узагальнити на довільну скінченну сукупність чисел. Добутком довільних цілих невід'ємних чисел a 1, a 2, …, an (позначається a 1 a 2… an або У шкільному курсі математики розглядається інше означення добутку цілих невід'ємних чисел, в основі якого лежить поняття суми. Нехай a i b – довільні цілі невід'ємні числа такі, що a = | A |, b = | B | і b > 1. За властивостями скінченних множин множина B є об'єднанням b одиничних множин, які попарно не перетинаються, тобто B = { y 1} { y 2} … { yb }. Тоді декартів добуток A B можна записати A B = A ({ y 1} { y 2} … { yb }). На основі дистрибутивного закону декартового множення відносно об'єднання множин A B = (A { y 1}) (A { y 2}) … (Α { yb }), де | A { yі }| = a ·1, і = 1, 2, 3…, b; (A { yi }) ∩ (A { yj }) = при i ≠ j, бо yi ≠ yj, i, j = 1, 2, …, b. Тому | A { yi }| = | A | = a i a · b = | A { y 1}| + | A { y 2}| + … + | A { yb }| = | A | + | A | + … + | A | = Звідси, враховуючи перші частини наслідків 6 і 7, одержуємо таке означення добутку двох цілих невід'ємних чисел.
Добутком довільних цілих невід'ємних чисел a i b (позначається a · b) називається: 1) число нуль, якщо b = 0; 2) число a, якщо b = 1; 3) число, яке є сумою b доданків, кожний з яких дорівнює a, якщо b > 1.
4. 1) комутативна: a, b N 0: a · b = b · a; 2) асоціативна: a, b, c N 0: (a · b)· c = a ·(b · c); 3) дистрибутивна відносно додавання: a, b, c N 0: (a + b)· c = a · c + b · c. 4) Наступні дві теореми пов'язують операцію множення цілих невід'ємних чисел з відношеннями рівності та порядку. Теорема 4 (закони монотонності множення). Операція множення цілих невід'ємних чисел монотонна: 1) відносно відношення рівності: a, b, c N 0: (a = b) → (a · c = b · c); 1) відносно відношень порядку, зокрема: a, b, c N 0: (a < b) (c ≠ 0) → (a · c < b · c). Теорема 5 (правила скорочення для множення). Для операції множення цілих невід'ємних чисел мають місце правила скорочення: 1) відносно відношення рівності: a, b, c N 0: (a · c = b · c) (c ≠ 0) → (a = b); 1) відносно відношень порядку, зокрема: a, b, c N 0: (a · c < b · c) (c ≠ 0) → (a < b).
5. У шкільному курсі розглядається означення добутку через суму, але вводиться воно у другому класі не все зразу, а частинами: спочатку дається означення: "Додавання однакових доданків називається множенням", потім: "При множенні довільного числа на одиницю одержується число, яке множили" і запис a ·1 = a. Нарешті, означення: "Добуток довільного цілого невід'ємного числа на нуль дорівнює нулю", запис a ·0 = a. Комутативний закон множення, який у школі називається переставним, вивчається до розгляду випадків множення на одиницю і нуль. Комутативний закон істотно використовується при складанні таблиці множення. Асоціативний закон множення розглядається також у початковій школі як правило множення добутку на число і числа на добуток. Дистрибутивний закон множення відносно додавання розглядається спочатку на конкретних прикладах і його називають правилом множення числа на суму і суми на число. Означення частки цілого невід’ємного і натуральних чисел. Умови існування частки, її єдність. Операція ділення на множині цілих невід’ємних чисел. Зв’язок ділення з множенням. Частка і ділення в початковому курсі математики. Нехай a = N(A) і множина A розбита на рівнопотужні підмножини без спільних елементів. Якщо b – число підмножин у розбитті множини A, то часткою чисел a і b називається число елементів кожної підмножини, тобто, число a потрібно зобразити у вигляді суми b однакових доданків, величину яких потрібно знайти: a = x + x +…+x (b доданків). Якщо b – число елементів кожної підмножини у розбитті множини A, то часткою чисел a і b називається число підмножин у цьому розбитті, тобто, знаходять кількість доданків, кожен з яких дорівнює b і сума яких a: a = b + b+ …+ b (x доданків). В обох випадкаах задача зводиться до знаходження невідомого множника за відомим добутком і другим множником, - дія ділення обернена до дії множення.
|
|||||||||
|
Последнее изменение этой страницы: 2021-01-14; просмотров: 419; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.93.136 (0.042 с.) |
 ) називається потужність декартового добутку множин A 1, A 2, …, An, потужностями яких є відповідно числа a 1, a 2, …, an.
) називається потужність декартового добутку множин A 1, A 2, …, An, потужностями яких є відповідно числа a 1, a 2, …, an.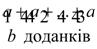 .
.