
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Прямокутна декартова система координат на площині. Паралельне перенесення початку координат. Відстань між двома точками на площині.Стр 1 из 8Следующая ⇒
Прямокутна декартова система координат на площині. Паралельне перенесення початку координат. Відстань між двома точками на площині. Декартова система координат на площині задається двома взаємно перпендикулярними осями (вісь ОХ – вісь абсцис, вісь ОУ – вісь ординат), які мають спільний початок О (початок координат) і однаковий масштаб осей. Кожній точці площини за певним правилом ставиться у відповідність пара чисел – абсциса та ордината (х;у), ці числа називаються декартовими координатами точки. Паралельне перенесення початку координат на площині. При перенесенні початку координат в точку 01 (a;в) без зміни координатного базису координати довільної точки площини обчислюються за формулами: Х/ = х - а, У/ = у - в. Приклад. А(2;-3) та В(-6;0) при перенесенні початку координат в точку 01 (-1;3). А: х = х-а = 2-(-1) = 3, у = у-в = -3-3=-6. А(3;-6). В: х = х-а = -6-(-1) = -5, у = у-в = 0-3=-3. В(-5;-3). Відстань між двома точками. Нехай на площині х0у задано дві точки А(Х1;у1) та В(х2;у2). Застосовуючи до прямокутного трикутника АВС теорему Піфагора, визначаємо відстань між точками А та В через координати цих точок: АВ2= (х2-х1)2 + (у2-у1)2, звідки |АВ|= (х2-х1)2 + (у2-у1)2.
Відношення еквівалентності. Зв’язок відношення еквівалентності з розбиттям множини на класи. Відношення еквівалентності в математиці – бінарне відношення.яке є рефлексивне,симетричне та транзитивне.Для того щоб відношення,було відношенням еквівалентності,повинні виконуватися всі три властивості..Приклади відношення еквівалентності. 1)Відношення рівності на довільній множині 2)Відношення паралельності прямих на площині 3)Відношення подібності на множині М усіх трикутників на площині За допомогою відношення еквівалентності виконується операція – розбиття множини на класи.Кожне розбиття S множини М визначаэ відношення еквівалентності.
Пряма пропорційність Лінійну функцію, що задається формулою, де, називають прямою пропорційністю.Графік прямої пропорційності — пряма, що проходить через початок координат. Обернена пропорційність Функцію, задану формулою, де х — незалежна змінна, — дане число, називають оберненою пропорційністю. Область визначення функції — множина всіх чисел, крім 0. Графік функції — гіпербола, симетрична відносно початку координат.
Лінійною називається функція, яку можна задати формулою, де х — аргумент, а k і b — дані числа. Графік лінійної функції — пряма. k називається кутовим коефіцієнтом прямої, яка є графіком лінійної функції. Кожна пряма на координатній площині, яка не є перпендикулярною до осі абсцис,— графік деякої лінійної функції.
Поняття про алгебраїчну операцію і алгебраїчну структуру. Закони алгебраїчних операцій. Нейтральний, поглинаючий, симетричний елементи. Приклади. Під алгебраїчною структурою розуміють деяку множину А із заданими на ній алгебраїчними операціями. Алгебраїчною операцією в множині Х називають відображення Х×Х―>Х,яке у відповідність кожній упорядкованій парі елементів (х,y)цієї множини ставить третій елемент z цієї ж множини. Позначають °,*... Приклади-Додавання в множині натуральних чисел N є алгебраїчною операцією, оскільки сума двох натуральних чисел є натуральне число. Для будь-яких множин A, B, та C, виконуються такі співвідношення: комутативність: · A ∪ B = B ∪ A · A ∩ B = B ∩ A асоціативність: · (A ∪ B) ∪ C = A ∪ (B ∪ C) · (A ∩ B) ∩ C = A ∩(B ∩ C) дистрибутивність операції перетину відносно об'єднання: · A ∪ (B ∩ C) = (A ∪ B) ∩(A ∪ C) · A ∩(B ∪ C) = (A ∩ B) ∪ (A ∩ C)
Елемент е називається нейтральним відносно операції °, якщо а°е=е°а=а(в додаванні -0,в множенні 1) Елемент w називається поглинаючим відносно операції °.якщо w °а=а° w = w.(у множенні -0) Нехай в множині Х,відносно алгебраїчної операції °,існує нейтральний елемент е. Елемент α називається симетричним елементу а відносно операції °.,а°α=α°а=е. В множині Z цілих чисел відносно операції додавання симетричним числу а є число -а оскільки а+(-а)=-а+а=0(0-нейтральний елемент відносно операції додавання).
Система аксіом Пеано За основні поняття цієї системи прийнято: а)основні обєкти – «ціле невідємне число», «нуль» б) основне відношення – «безпосередньо слідує за» Аксіома 1. Нуль є ціле невідємне число, що не слідує за жодним іншим цілим невідємним числом.
Аксіома 2. Яке б не було ціле невідємне число а, існує єдине ціле невідємне число а´, що безпосередньо слідує за а Аксіома 3. Яке б не було ціле невідємне число а, існує єдине ціле невідємне число b, за яким а безпосередньо слідує Аксіома 4. (аксіома індукції) Якщо будь яки підмножина М множина цілих невідємних чисел має властивості: 1) містить нуль, 2) якщо вона містить ціле невідємне число а´, то дана множина М збігається з множиною цілих невідємних чисел. На принципі математичної індукції грунтується метод матиматичної індукції. Доведення методом матиматичної індукції складається з трьох частин: · Перевіряємо істинність твердження для n=1; · Припускаємо, що твердження істинне для деякого n=k та доводимо, що воно буде істинним і для безпосередньо наступного n=k´
Означення різниці двох цілих невід’ємних чисел. Умови існування різниці, її єдиність. Операція віднімання на множині цілих невід’ємних чисел. Зв’язок віднімання з додаванням. Поняття різниці і віднімання в початковому курсі математики. 1.Різницею цілих невід’ємних чисел a і b називається число с, яке є потужністю доповнення підмножини В до множини А: а – b = c N(A) – N(B) = N(B᷃A) Число а називають зменшуваним, b – від’ємником, с – різницею, а операцію знаходження різниці – дією віднімання. 2. Теорема 10. Для довільних цілих невід'ємних чисел a та b їх різниця існує тоді і тільки тоді, коли a ≥ b. Якщо різниця цілих невід'ємних чисел існує, то вона єдина. ► І. Доведемо існування різниці. 1) Нехай a ≥ b. Можливі два випадки або a = b, або a > b. Якщо a = b, то за властивістю нуля при додаванні будемо мати b + 0 = a. Звідси за означенням різниці одержуємо a – b = 0. Якщо ж a > b, то за означенням відношення "більше" дістанемо b x = a, де x N. Звідси за означенням різниці a – b = x. 2) Нехай різниця цілих невід'ємних чисел a та b існує. Покажемо, що a ≥ b. Дійсно, оскільки різниця цілих невід'ємних чисел a і b існує, то за означенням різниці знайдеться ціле невід'ємне число x таке, що b + x = a. Для x можливі два випадки: або x = 0, або x ≠ 0 (тобто, x N). Якщо x = 0, то з того, що b + 0 = a, випливає (за властивістю нуля при додаванні) b = a. Якщо ж x N, то з того, що b + x = a, одержуємо (за означенням відношення "більше") a > b. А тому маємо, що при існуванні різниці чисел a і b, a ≥ b. Отже, існування різниці доведено. ІІ. Доведемо єдиність різниці. Нехай різниця цілих невід'ємних чисел a і b існує. Припустимо, що a − b = x 1, і a – b = x 2. Звідси за означенням різниці маємо a = b + x 1 і a = b + x 2. Отже, b + x 1 = b + x 2 і за правилом скорочення для додавання одержимо x 1 = x 2. Значить, різниця цілих невід'ємних чисел, якщо вона існує, визначається однозначно. ◄ З доведеної теореми одержуємо наслідок. Наслідок 5. a 0: a – 0 = a; a 0: a – a = 0. 3. Операція у множині цілих невід'ємних чисел, при якій кожній парі чисел a і b ставиться у відповідність їх різниця a – b, називається відніманням цілих невід'ємних чисел. Компоненти віднімання називаються: перша – зменшуваним, друга – від'ємником, а результат – різницею. 4. На підставі означення різниці через суму одержуємо, що віднімання цілих невід'ємних чисел є оберненою операцією до додавання. А теорема 10 показує, що віднімання є частковою операцією для цілих невід'ємних чисел. Оскільки А = В ∪ B᷃A і В ⋂ B᷃A = ∅, за означенням суми цілих невід’ємних чисел N(A) = N(B) + N(B᷃A), тобто a = b + c. Отже віднімання – дія обернена до дії додавання.
5. У шкільній математиці віднімання вводиться на основі практичних вправ, пов'язаних з виділенням підмножини даної множини і утворення нової множини – доповнення виділеної підмножини. При цьому, звичайно, теоретико-множинна символіка і термінологія не використовуються, а число елементів підмножини і її доповнення знаходяться способом переліку. Головним засобом розкриття теоретико-множинного смислу віднімання є розв'язування простих задач. Зв'язок віднімання з додаванням встановлюється при розгляді теми "як знайти невідомий доданок". Означення віднімання, як операції оберненої до додавання, в явному виді не дається, але постійно використовується. Правила віднімання числа від суми і суми від числа вводяться ще у першому класі, по суті, на теоретико-множинній основі. Приклади, які розглядаються при цьому, ілюструються наочністю.
Означення добутку двох цілих невід’ємних чисел. Існування добутку, його єдиність. Операція множення на множині цілих невід’ємних чисел. Закони множення: комутативний, асоціативний, дистрибутивний відносно додавання. Поняття добутку і множення в початковому курсі математики. 1.Добуток цілих невід’ємних чисел позначається через декартовий добуток множин та через суму однакових доданків. Означення 1. Добутком цілих невід’ємних чисел m і k називається число елементів декартового добутку множини що має m елементів на множину що має k елементів. Означення 2. Добутком цілого невід’ємного числа m на натуральнее число k називається сума k доданків кожен з яких дорівнює m m*k = m+m+….+m } k Числа m і k називають множниками, а операцію знаходження добутку – дію множення. Добуток цілого невід’ємного числа числа а на 1 є число а: (∀а є N0) а *1=а Добуток цілого невід’ємного числа а на 0 є нуль: (∀а є N0) а*0=0 2. Теорема 6. (про існування та єдиність добутку): якими б не були цілі невід’ємні числа a і b завжди існує єдине ціле невід’ємне число a×b, яке є їх добутком. Доведення: Для доведення теореми використаємо означення добутку через суму однакових доданків, розглянувши три випадки: 1) b=0; 2) b=1; 3) b>1. Якщо b=0, то добуток а×0 існує згідно з додатковим означенням: а×0=0. Якщо b=1, то добуток а×1 також існує згідно з додатковим означенням: а×1=а. В обох випадках добутки єдині. Якщо b>1, то добуток існує і єдиний, бо існує і єдина сума а+а+а+...+а=а×b. Теорему доведено.
3. Поняття добутку двох цілих невід'ємних чисел можна узагальнити на довільну скінченну сукупність чисел. Добутком довільних цілих невід'ємних чисел a 1, a 2, …, an (позначається a 1 a 2… an або У шкільному курсі математики розглядається інше означення добутку цілих невід'ємних чисел, в основі якого лежить поняття суми. Нехай a i b – довільні цілі невід'ємні числа такі, що a = | A |, b = | B | і b > 1. За властивостями скінченних множин множина B є об'єднанням b одиничних множин, які попарно не перетинаються, тобто B = { y 1} { y 2} … { yb }. Тоді декартів добуток A B можна записати A B = A ({ y 1} { y 2} … { yb }). На основі дистрибутивного закону декартового множення відносно об'єднання множин A B = (A { y 1}) (A { y 2}) … (Α { yb }), де | A { yі }| = a ·1, і = 1, 2, 3…, b; (A { yi }) ∩ (A { yj }) = при i ≠ j, бо yi ≠ yj, i, j = 1, 2, …, b. Тому | A { yi }| = | A | = a i a · b = | A { y 1}| + | A { y 2}| + … + | A { yb }| = | A | + | A | + … + | A | = Звідси, враховуючи перші частини наслідків 6 і 7, одержуємо таке означення добутку двох цілих невід'ємних чисел. Добутком довільних цілих невід'ємних чисел a i b (позначається a · b) називається: 1) число нуль, якщо b = 0; 2) число a, якщо b = 1; 3) число, яке є сумою b доданків, кожний з яких дорівнює a, якщо b > 1.
4. 1) комутативна: a, b N 0: a · b = b · a; 2) асоціативна: a, b, c N 0: (a · b)· c = a ·(b · c); 3) дистрибутивна відносно додавання: a, b, c N 0: (a + b)· c = a · c + b · c. 4) Наступні дві теореми пов'язують операцію множення цілих невід'ємних чисел з відношеннями рівності та порядку. Теорема 4 (закони монотонності множення). Операція множення цілих невід'ємних чисел монотонна: 1) відносно відношення рівності: a, b, c N 0: (a = b) → (a · c = b · c); 1) відносно відношень порядку, зокрема: a, b, c N 0: (a < b) (c ≠ 0) → (a · c < b · c). Теорема 5 (правила скорочення для множення). Для операції множення цілих невід'ємних чисел мають місце правила скорочення: 1) відносно відношення рівності: a, b, c N 0: (a · c = b · c) (c ≠ 0) → (a = b); 1) відносно відношень порядку, зокрема: a, b, c N 0: (a · c < b · c) (c ≠ 0) → (a < b).
5. У шкільному курсі розглядається означення добутку через суму, але вводиться воно у другому класі не все зразу, а частинами: спочатку дається означення: "Додавання однакових доданків називається множенням", потім: "При множенні довільного числа на одиницю одержується число, яке множили" і запис a ·1 = a. Нарешті, означення: "Добуток довільного цілого невід'ємного числа на нуль дорівнює нулю", запис a ·0 = a. Комутативний закон множення, який у школі називається переставним, вивчається до розгляду випадків множення на одиницю і нуль. Комутативний закон істотно використовується при складанні таблиці множення. Асоціативний закон множення розглядається також у початковій школі як правило множення добутку на число і числа на добуток. Дистрибутивний закон множення відносно додавання розглядається спочатку на конкретних прикладах і його називають правилом множення числа на суму і суми на число.
Означення частки цілого невід’ємного і натуральних чисел. Умови існування частки, її єдність. Операція ділення на множині цілих невід’ємних чисел. Зв’язок ділення з множенням. Частка і ділення в початковому курсі математики. Нехай a = N(A) і множина A розбита на рівнопотужні підмножини без спільних елементів. Якщо b – число підмножин у розбитті множини A, то часткою чисел a і b називається число елементів кожної підмножини, тобто, число a потрібно зобразити у вигляді суми b однакових доданків, величину яких потрібно знайти: a = x + x +…+x (b доданків). Якщо b – число елементів кожної підмножини у розбитті множини A, то часткою чисел a і b називається число підмножин у цьому розбитті, тобто, знаходять кількість доданків, кожен з яких дорівнює b і сума яких a: a = b + b+ …+ b (x доданків). В обох випадкаах задача зводиться до знаходження невідомого множника за відомим добутком і другим множником, - дія ділення обернена до дії множення.
Поняття про систему числення. Позиційні і непозиційні системи числення. Запис чисел у позиційних системах числення. Дії над числами в позиційних системах числення. Перехід від запису чисел в одній системі числення до запису в другій. Системою числення (нумерації) називається сукупність правил і знаків або слів, за допомогою яких можна образити письмово або назвати будь-яке натуральне число. Непозиційні системи числення (єгипетська, римська, давньогрецька,слов’янська) не пристосовані для виконання арифметичних дій на письмі, в них не можна записувати великі числа Позиційні системи числення відрізняються тим, що в них один і той самий знак(цифра) означає рівні числа в залежності від розташування його в записі числа.Завдяки цьому, як завгодно велике число може бути записане за допомогою скінченної кількості знаків. Для того, щоб натуральне число, записане в десятковій системі числення подати у позиційній системі числення з основою g,треба поділити це число на основу g,частку знову поділити на g і т.д. поки не дістанемо частку меншу g.Утворені при цьому послідовні остачі будуть цифрами даного числа, записанго при основі g: перша остача-цифрою одиницт,друга-цифрою одииниць другого розряду і тд.Остання частка буде цифрою одиницт найвищого розряду шуканого числа. Із позиційного принципу запису чисел у системах числення з основою g де g ≠10, випливають письмові алгоритми арифметичних дій, цілком аналогічні відповідним алгоритмам у десятковій системі числення При додаванні(відніманні) багатоцифрових чисел потрібно підписувати їх так, щоб відповідні розряди були написані один під другим і починати додавати(віднімати) з нижчих розрядів. Алгоритм множення чисел у будь-якій системі числення з основою g такий же, як у десятковій системі числення: можна множити одноцифрові числа в десятковій системі числення, а для запису кожний добуток переводити в систему чилсення з основою g. Для того,щоб будь-яке число аg, де g≠10,записати в десятковій системі числення, потрібно подати його у вигляді суми розрядних одиниць, усно виразити всі цифри і основу g у десятковій системі числення і виконати обчислення 27. Відношення подільності на множині натуральних чисел, його властивості. Означення. Говорять, що ціле невід’ємне число а ділиться на натуральне число b, якщо існує таке ціле невід’ємне число q, що а = bq. Говорять «число а кратне числу b». Відношення подільності числа a на число b символічно позначають а Чисел, кратних даному числу – нескінченна множина. Наприклад, усі парні числа кратні числу 2. Їх можна знайти за формулою х = 2∙ q, де q набуває значення 0, 1, 2, 3,.... Число 1 ділиться тільки само на себе; числа 2, 3, 5, 7,... діляться самі на себе і на одиницю; числа 4, 6, 8, 9,... мають більше двох дільників. Ці спостереження привели математиків до введення понять простого і складеного числа. Означення. Натуральне число, яке має лише два дільники, називається простим. Отже, числа 2, 3, 5, 7 – прості числа. Означення. Натуральне число, яке має більше двох дільників, називається складеним. Властивості подільності чисел Подільність суми. (достатня умова) Якщо числа a і b діляться на c,то їх сума ділиться на с Подільність різниці (достатня умова) Якщо один з множників ділиться на натуральне число с, то й добуток ділиться на це число (нобхідна і достатня умова) Добуток ділиться на число с тоді і тільки тоді, коли на с ділиться добуток остач від ділення кожного із співмножників на число с Подільність добутку (достатня умова) Якщо один із множників ділиться на натуральне число с то й добуток ділиться на це число (Необхідна і достатня умова) Добуток ділиться на число с тоді і тільки тоді,коли на с ділиться добуток остач від ділення кожного із співмножників на число с
Вимірювання довжини відрізка, неспільномірного з одиничним відрізком. Нескінченні десяткові дроби. Ірраціональні числа. Запис додатного дійсного числа. Відношення порядку на множині додатних дійсних чисел. Процес вимірювання довжини відрізка полягає у послідовному відкладанні одиничного відрізка і його частин на даному відрізку, довжину якого ми вимірюємо. Звичайний нескоротний дріб, до канонічного розкладу якого входить принаймні один простий множник, відмінний від 2 і 5, зображують нескінченим десятковим дробом. Ірраціональним числом називають нескінченни неперіодичний десятковий дріб. Множину додатних ірраціональних чисел позначають I+. Множина додатних дійсних чисел R+ називають об'єднання множини Q+ і I+. Відношення порядку на множені додатніх дійсних чисел -напр. є два числа 1,0987 і 1,0997,відносно порядку чиисел ми дивимось, яке число більше.
Вимірювання довжин та площ. Процес вимірювання довжини відрізка полягає у послідовному відкладанні одиничного відрізка і його частин на даному відрізку, довжину якого ми вимірюємо. Способи вимірювання площ: 1)за допомогою палетки; 2)за відомими формулами: Sпрямокутника=a
Прямокутна декартова система координат на площині. Паралельне перенесення початку координат. Відстань між двома точками на площині. Декартова система координат на площині задається двома взаємно перпендикулярними осями (вісь ОХ – вісь абсцис, вісь ОУ – вісь ординат), які мають спільний початок О (початок координат) і однаковий масштаб осей. Кожній точці площини за певним правилом ставиться у відповідність пара чисел – абсциса та ордината (х;у), ці числа називаються декартовими координатами точки. Паралельне перенесення початку координат на площині. При перенесенні початку координат в точку 01 (a;в) без зміни координатного базису координати довільної точки площини обчислюються за формулами: Х/ = х - а, У/ = у - в. Приклад. А(2;-3) та В(-6;0) при перенесенні початку координат в точку 01 (-1;3). А: х = х-а = 2-(-1) = 3, у = у-в = -3-3=-6. А(3;-6). В: х = х-а = -6-(-1) = -5, у = у-в = 0-3=-3. В(-5;-3). Відстань між двома точками. Нехай на площині х0у задано дві точки А(Х1;у1) та В(х2;у2). Застосовуючи до прямокутного трикутника АВС теорему Піфагора, визначаємо відстань між точками А та В через координати цих точок: АВ2= (х2-х1)2 + (у2-у1)2, звідки |АВ|= (х2-х1)2 + (у2-у1)2.
|
|||||||||
|
Последнее изменение этой страницы: 2021-01-14; просмотров: 171; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.13.255 (0.089 с.) |
 ) називається потужність декартового добутку множин A 1, A 2, …, An, потужностями яких є відповідно числа a 1, a 2, …, an.
) називається потужність декартового добутку множин A 1, A 2, …, An, потужностями яких є відповідно числа a 1, a 2, …, an.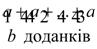 .
.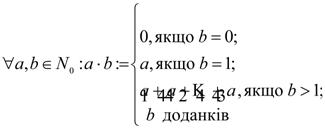
 b. Відношення подільності не означає операції, тому не можна писати а
b. Відношення подільності не означає операції, тому не можна писати а  b;Sпаралелограма=a
b;Sпаралелограма=a  ; Sтрикутника =
; Sтрикутника = 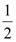 aha =
aha = 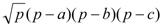 , де p=
, де p=  .
.


