
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Лабораторная работа 10. Метод наименьших квадратов ⇐ ПредыдущаяСтр 9 из 9
В ЛИНЕЙНОЙ МОДЕЛИ ИЗМЕРЕНИЙ Предположим, что вектор результатов измерений Y =[ y 1,…, yn ] T имеет следующую структуру: Y = A Θ+ E, (10.1) где Θ = [ θ 1,…, θr ] T – вектор неизвестных, но вполне определенных параметров, подлежащий оцениванию; A = [ aij ] – известная матрица размерности n × r, r ≤ n, имеющая максимально возможный ранг r; E =[ ε 1,…, εn ] T – вектор случайных погрешностей измерений. Предположим, что компоненты вектора E – независимые случайные величины со средним 0 и дисперсией σ 2: ME =0, cov(E)= σ 2 I, где I – единичная матрица. Такая схема связи результатов измерений (откликов) и неизвестных параметров (факторов) называется линейной моделью измерений. Будем искать оценку вектора Θ из условия
Такой подход к оцениванию неизвестных параметров называется методом наименьших квадратов (МНК). Найдем производную
откуда
Оценка
Таким образом,
Если вектор случайных погрешностей измерений E является гауссовым,
Если дисперсия σ2 неизвестна, то можно использовать ее несмещенную оценку
которая в гауссовом случае оказывается независимой от В гауссовом случае оценка по МНК является оценкой максимального правдоподобия и, тем самым, обладает целым рядом важнейших свойств эффективности. В негауссовых ситуациях при весьма общих предположениях о законе распределения погрешностей измерений она остается эффективной в классе оценок, линейных по y 1,…, yn, но, например, соотношение (10.3) выполняется лишь асимптотически при Если в модели (10.1) погрешности измерений коррелированны, cov(E) = Σ, где Σ –симметричная невырожденная положительно-определенная матрица (все ее собственные числа строго больше нуля), то обе части (1) можно домножить на Σ-1/2:
В преобразованной таким образом модели вектор погрешностей Σ-1/2 E по-прежнему имеет среднее 0, но является некоррелированным: cov(Σ-1/2 E) = M [(Σ-1/2 E) (Σ-1/2 E) T ] = Σ-1/2 M (EET) Σ-1/2 Применяя к модели (5) оценку (2), получаем
Оценку Замечание. В качестве матрицы Σ-1 в (10.5) часто берут диагональную матрицу, диагональные элементы которой (весовые коэффициенты) отражают степень доверия к тому или иному измерению: чем менее достоверно измерение, тем меньше соответствующий весовой коэффициент. Как всякая линейная функция результатов измерений, оценка (10.2) может вычисляться рекуррентно, в реальном масштабе времени, подвергаясь уточнению по мере появления каждого нового измерения. Пусть
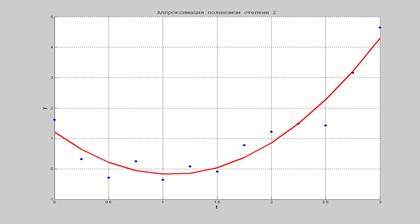
(рекуррентный МНК). В качестве начального приближения Примеры 1. Полиномиальное сглаживание. Результаты измерений yi, проведенных в моменты времени ti, i =1,…, n, приведены в табл. 1. Предполагается, что их можно аппроксимировать полиномом заданной степени r =2. Требуется получить на основе МНК оценки коэффициентов этого полинома. Таблица 1
Решение. Модель измерений имеет вид
где a 0,…, ar – искомые коэффициенты (r =2). Поскольку речь идет о применении МНК, погрешности ε i можно считать некоррелированными и приближенно нормальными с нулевым средним и дисперсиями, которые, в отсутствие дополнительной информации, естественно считать равными. В матричной форме эти соображения приводят к модели (10.1), где aij = [ ti j ], Θ=[ a 0,…, ar ] T.
Пример выполнения работы
Замечание. В ИМС MatLab есть готовая процедура-функция p =polifit(t, y, r), решающая задачу аппроксимации пар точек (ti, yi) полиномом степени r, где p – вектор коэффициентов полинома в порядке понижения степени r.
Рис.10.1. Полиномиальное сглаживание
2. Оценивание параметров гармонического сигнала. Гармонический сигнал с известной частотой ω и неизвестными амплитудой A и фазой φ измеряется с аддитивной гауссовой ошибкой в моменты времени ti, i =1,…, n. Требуется получить на основе МНК оценки амплитуды и фазы сигнала. Решение. Модель измерений yi, i =1,…, n имеет вид
или, в векторной форме, Y = A Θ + E, Y = [ y 1,…, yn ] T,
МНК-оценка вектора Θ получается по формуле (2), оценка дисперсии измерений σ 2 – по формуле (4). Далее,
Задачи для самостоятельного решения 1. Модель измерений в обычных вероятностных предположениях имеет вид yi = ati+ε i, i =1,…, n, a – скалярный параметр, подлежащий оцениванию. Найти МНК- оценку 2. Построить рекуррентный алгоритм вычисления оценки 3. В схеме задачи 10.3 рассматриваются две линейных модели с независимыми погрешностями измерений, имеющими нулевые средние и одинаковые дисперсии σ 2: yi = ati+ε i, i =1,…, n, zj = bti+ηi, i =1,…, m, причем известно, что a + b = c, c – известная постоянная величина. Требуется получить МНК-оценки параметров a, b. Минимизировать общую сумму квадратов невязок G (a, b) при ограничении a + b = c, используя метод неопределенных множителей Лагранжа.
ПРИЛОЖЕНИЕ 11. Статистические методы в экспертных оценка x Слова «экспертные оценки» в последнее время приобрели популярность. Одни готовы прибегать к экспертному методу в случае любого затруднения. Другие считают его вредной выдумкой, мода на которую скоро пройдет. Такого разнообразия во мнениях не бывает о предметах привычных, и можно подумать, что экспертные методы - недавнее изобретение. Это и так, и не так. К мнению специалистов (т. е. экспертов) при решении сложных вопросов обращались всегда, и в этом нет ничего нового. Новым является лишь то, что этому опросу придают заранее и тщательно продуманную форму, организуют этот опрос определенным образом. Традиционный способ знакомства с мнением специалистов - совещание. Его достоинства очевидны - это возможность не только высказать мнение, но и аргументированно его защитить или оспорить. В результате решение может быть принято после тщательного обсуждения; это уменьшает возможность ошибок. Но совещание как метод экспертного опроса имеет свои недостатки: на нем может возобладать мнение какого-либо одного участника в силу влияния, которое он может оказать на других - с помощью своего выдающегося красноречия, авторитета, служебного положения и т. п.
Нередко поэтому предпочитают индивидуальный опрос специалистов. Обсуждение проводится лишь на последующих стадиях и в ограниченных размерах. Пример такой методики дает широко известный метод «Делфи». Метод был придуман при попытках угадать даты крупных прорывов в области управляемого термоядерного синтеза. К сожалению, пока ничего из предсказанного не сбылось. Возможно, это пример неоправданного расширения сферы приложения метода. Экспертные методы широко распространены в практике, хотя представляют лишь один из примеров тех задач, в которых источником информации является человек. Постоянно проводятся экспертизы по оценке качества потребительских товаров. Судейство некоторых видов спортивных соревнований (гимнастика, фигурное катание на коньках) тоже основано на экспертных методах. Все чаще проводят опросы различных групп населения для выяснения общественного мнения по томуили иному вопросу. Результаты при этом фиксируются не с помощью приборов, а по ответам человека - испытуемого. Главная особенность человека как источника информации состоит в том, что он плохо отвечает на вопросы количественного характера и гораздо лучше на вопросы качественного, сравнительного характера. Например, человеку трудно оценить на глаз расстояние до далекого предмета, но гораздо легче сказать, какой из двух предметов ближе. Трудно оценить вес камня, но легко сказать, какой из двух камней легче и т. д. В некоторых случаях количественные характеристики объектов и вовсе невозможны, доступны только качественные. Скажем, из двух образцов пасты для зубов можно выбрать лучший, но очень сложно количественно оценить их достоинства. Итак, в правильно построенном экспертном опросе поступающая информация обычно носит качественный, сравнительный характер. В каждой экспертизе исследователь, учитывая цели опроса и возможности экспертов, может использовать специальные варианты вопросов. Можно, однако, указать определенный набор наиболее употребительных. Парные сравнения. Из данной совокупности объектов поочередно выбираются пары объектов. Сравнивая выбранные объекты, человек для каждой пары решает, какой из объектов лучше (обладает более ярко выраженным заранее оговоренным свойством). Можно поставить задание и по-иному — попросить испытуемого отвечать на вопрос о сходстве этих объектов; допускаются ответы «похожи», «не похожи». Можно сравнивать выбранные объекты с контрольным образцом; задание - указать, который из двух объектов более похож на контрольный, и т. д.
Множественные сравнения. Из совокупности поочередно выбираются уже не пары, а наборы из нескольких объектов. Задания те же, что и при парном сравнении. Ранжирование. Все объекты совокупности выстраиваются по возрастанию (или убыванию) оговоренного признака. Классификация. Вся совокупность объектов разделяется экспертом на несколько классов. Классы могут быть определены заранее, но могут и формироваться в процессе экспертизы. Список этот нетрудно продолжить. Вошедшие в него вопросы достаточно просты и потому допускают математическую трактовку. Мы займемся задачей упорядочения, поскольку для ее решения можно использовать уже знакомый аппарат рангов. Действительно, при упорядочении каждый объект получает номер, т. е. ранг. Задача состоит в том, чтобы по совокупности данных экспертами упорядочений составить усредненное упорядочение, наиболее близкое к истинному. Введем необходимые обозначения. Прежде всего, произвольным образом занумеруем все объекты числами от 1 до п. Этой нумерации будем держаться в дальнейшем. Каждому из экспертов, которых тоже пронумеруем, независимо от других предлагаем упорядочить весь набор объектов. Дележ мест не допускается. В результате получаем матрицу целых чисел К ее решению сейчас существуют два подхода. Первый подход предлагает искать компромиссную точку зрения - нечто вроде равнодействующей всех высказанных мнений. Это мнение - в определенном смысле ближайшее к совокупности высказанных. Математическое оформление этого замысла составляет содержание первого подхода - алгебраического. Второй подход имеет статистический характер. Каждую данную экспертом ранжировку мы считаем несовершенным, искаженным вариантом правильного упорядочения. Ошибки, совершаемые разными экспертами при упорядочении, возникают случайно, в том смысле, какой принято придавать этому слову в математической статистике. Несколько вольно выражаясь, можно сказать, что при статистическом подходе каждого эксперта предлагается рассматривать как некий измерительный «прибор», показания которого сопровождаются случайной ошибкой. Эта аналогия хотя и полезна, но является довольно далекой. Прежде всего «показания эксперта как прибора» имеют не числовой характер, эксперт дает только порядок объектов. Закон распределения случайной ошибки изучить довольно трудно, так как почти невозможны независимые повторные измерения - высказавшись однажды о порядке объектов, эксперт едва ли изменит свою точку зрения при повторном опросе.
В дальнейшем нас будет в основном интересовать статистический подход. Но прежде чем перейти к нему, наметим кратко линию исследований в алгебраическом подходе. Как уже говорилось, в этом подходе предлагается найти упорядочение, в каком-то смысле ближайшее к набору Английские математики Кемени и Снелл предложили ряд простых и естественных свойств, которым должно удовлетворять любое расстояние между перестановками. Оказалось, что существует лишь одна функция Определяется она любопытным образом. Для каждой перестановки определяется матрица, элементами которой служат числа 1 или 0. Элемент матрицы с номером (i, j) равен +1, если ранг объекта i меньше ранга объекта j, т. е. если объект i идет в упорядочении прежде объекта j. В противном случае этот элемент равен 0. Диагональные элементы матрицы можно не определять. Обозначим через || ai j || такую матрицу, построенную по перестановке A, через || bi j ||— по перестановке В. Теперь введенное Кемени и Снеллом расстояние Используя это расстояние, можно определить нечто вроде «центра» всех высказанных мнений, выбрав в этом качестве такую перестановку, сумма расстояний от которой до всех экспертных перестановок Ясно, что вычисление A0 в случае больших т, п представляет значительные вычислительные трудности. Легко представить себе наглядно, что такое расстояние между перестановками. Пусть буквами a, b, c, d,… обозначены объекты. Будем называть две перестановки соседями (или соседними), если одна получается из другой переменной порядка двух рядом стоящих объектов. Например, соседями являются перестановки abc и bac, dabc и dacb и т. д. В то же время abc и cba соседями не являются, так же как dabc и adcb. Теперь изобразим каждую из n! перестановок точкой пространства. Соседние перестановки соединим отрезками единичной длины. Конструкции такого рода, состоящие из точек, называемых вершинами, и ребер, т. е. соединяющих некоторые точки отрезков, называют графами. В случае n = 3образующуюся конфигурацию - правильный шестиугольник - можно изобразить на плоскости. Для n = 4 объектов получается пространственная фигура — усеченный октаэдр. При больших п соответствующие графы нельзя нарисовать без искажений масштаба. Оказывается, расстояние Кемени-Снелла между любыми двумя перестановками равно длине кратчайшего пути по соответствующему графу. Расстояние Кемени-Снелла Поэтому медиана Кемени—Снелла может определяться и иначе, как такое A0, что т. е. как последовательность A0, в среднем наиболее коррелированная (по Кендаллу) с совокупностью Впрочем, в математической статистике более популярен коэффициент ранговой корреляции по Спирмену, традиционно обозначаемый ρ. Выберем для ρ форму, наиболее схожую с (11.2). Если Сумма S (А, В)= Оказывается, что соответствующий A0 порядок следования объектов может быть указан явно. Для этого от матрицы рангов || ri j || надо перейти к последовательности средних рангов. Мы смотрим на данное экспертом упорядочение как на отражение объективной закономерности, как на ее реализацию, хотя и несовершенную, содержащую ошибки. Поскольку все экспертные упорядочения отражают одну закономерность, между ними в целом и попарно должно наблюдаться какое-то сходство. Существование такого сходства мы хотим выявить предварительным анализом. Последующая же обработка должна быть направлена на выявление той закономерности, которую отражают отдельные упорядочения. Для измерения сходства двух упорядочений естественно использовать коэффициенты ранговой корреляции. На практике обычно используют коэффициенты Кендалла τ и Спирмена ρ, причем теория в обоих случаях идет параллельно. Происхождение коэффициента ρ легко объяснить. Перепишем ранее данную для ρ формулу (16.3) в виде Знаменатель этой дроби является просто другим выражением для сумм Величина Следовательно, ρ (A, B) есть просто выборочный коэффициент корреляции, рассчитанной по совокупности п пар (ri, si), i =1, …, n. Обратим внимание на то, что значение ρ (равно как и τ) не зависит от первоначально выбранной нумерации; оно остается одним и тем же при любой нумерации объектов. Коэффициент ранговой корреляции ρ был впервые применен Спирменом много лет назад, когда он пытался обнаружить связи между двумя признаками, не допускающими точного количественного выражения. Допустим, речь идет об успехах детей в учебе и спорте. Можно составить два списка учащихся класса, в которых фамилии пойдут в порядке успеваемости и спортивных показателей. Возьмем за основу нумерацию, данную первым списком. Номера во втором списке окажутся при этом рангами, которые учащиеся получают при упорядочении по второму признаку. Если между двумя признаками нет никакой зависимости, не будет никакой связи и между номерами в двух списках. Это означает, что в качестве второй нумерации с равными шансами может появиться любая, т. е. вторая нумерация окажется чисто случайной по отношению к первой. Распределения коэффициентов ρ и τ в условиях чистой случайности может быть вычислено при малых численностях группы объектов п. В случае ρ для n ≤ 11 и в случае τ для n ≤ 12 имеются таблицы распределения вероятностей тесно связанных с ρ и τ величин. Например, вместо ρ табулировано распределение статистики При больших значениях n возникает вопрос о подходящем приближении для распределения ρ. Доказано, что закон распределения случайной величины Если упорядочения по двум признакам каким-либо образом связаны, коэффициенты ρ и τ обнаруживают тяготение к положительным значениям, если большая выраженность одного признака сопутствует большему проявлению другого, и к отрицательным в противном случае. Проверку гипотезы об отсутствии связи между двумя признаками (о независимости признаков, как еще говорят) можно провести, оценивая значимость отклонения ρ (или τ) от нуля. Если подозревается положительная связь, вычисляют При числе ранжировок более двух независимость признаков, т. е. чистая случайность всех нумераций по отношению друг к другу, может быть проверена с помощью предложенного Кендаллом коэффициента конкордации W. Сам Кендалл предложил для W формулу Поскольку справедливо неравенство знаменатель этой дроби не меньше числителя. Они равны, если все нумерации совпадают. При этом W =1. Если различия между ранжировками велики, суммы рангов окажутся более или менее близки друг к другу по величине, и поэтому числитель будет мал по сравнению со знаменателем. Коэффициент конкордации будет при этом близок к нулю. Увеличение W от 0 до 1 означает, что согласованность между ранжированиями усиливается. Как обычно, появившаяся в эксперименте значимо отличающаяся от нуля величина W свидетельствует против гипотезы о чистой случайности. С выражением, стоящим в знаменателе дроби (16.5), мы уже встречались при обсуждении ρ. Заменяя знаменатель его значением (которое неизменно при всех ранжированиях), получаем для W выражение Конечно, близкое к нулю значение W не доказывает, что признаки независимы. Так, для двух полностью противоположных упорядочений W оказывается в точности равным нулю, а коэффициент корреляции | ρ |=1. Обратим внимание на связь W с парными коэффициентами корреляции по Спирмену. Нетрудно доказать, что т. е. W есть средний по всей совокупности коэффициент ранговой корреляции по Спирмену. Аналогичные результаты можно получить и при использовании τ Кендалла. В частности, в качестве меры согласия может употребляться тем же Кендаллом предложенный коэффициент U, очень незначительно отличающийся от среднего значения τ: Максимальное значение U равно 1. Оно достигается при совпадении всех ранжировок. Минимальное значение U, к сожалению, отличается от нуля, хотя и немного. Конечно, вычислять U значительно труднее, чем W. По-видимому, по этой причине он употребляется реже. Как можно использовать эти величины в экспертном ранжировании? Можно вычислить W по всей совокупности ранжировок, которой мы располагаем. Если эта величина, которую обозначим W *, оказывается близкой к нулю, т. е. если мала Причиной того, что выборочное значение W мало и, следовательно, экспертные мнения плохо согласованы, может быть отсутствие объективной основы для сравнения объектов, для их упорядочения. Другой причиной может быть неоднородность экспертной группы, в которой присутствуют представители нескольких точек зрения. При механическом сложении различные мнения уравновешиваются, и компромиссного упорядочения не находится. В большинстве случаев на практике выборочные значения W далеко превосходят критические. Как правило, это не приносит особого удовлетворения, так как до всякого опыта мы были убеждены, что тот набор объектов, с которым мы имеем дело, упорядочить можно. Вопрос не в этом, а в том, каков правильный порядок. В литературе по экспертному оцениванию приходится порой сталкиваться и с такой рекомендацией: для повышения надежности результатов усреднения предварительно выделить из всей группы экспертов более узкую подгруппу с высоким коэффициентом W. Усреднение затем производить по этой подгруппе, а не вошедшие в эту подгруппу ранжировки не принимать во внимание, отбросить. Возможно, это неплохая рекомендация. К сожалению, научные основания ее довольно туманны, да и вычислительные трудности велики. Кроме упорядочения по средним рангам и медианы Кемени - Снелла, используют и другие методы. В рамках статистического подхода они находят свое объяснение. Упомянем квантильный метод, в котором экспертная информация представляется особенно наглядно. В этом методе для каждого объекта A (j) строится кривая накопленных частот, и эти кривые далее сравниваются между собой. Кривая накопленных частот объекта A (j) строится следующим образом. Сначала подсчитываем, сколько раз при т ранжированиях объект A (j) занимал первое место. Получаем число G 1. Затем подсчитываем, сколько раз объект A (j) занимал место не ниже второго, т. е. сколько раз он был признан первым либо вторым. Получаем число G 2, G 2≥ G 1.. Продолжая этот процесс обычным образом, подсчитываем последовательно, сколько раз объект A (j) занимал место не ниже k, k =1, 2, …, n. Получаем последовательность чисел G 1, G 2, …, Gn. Далее на координатной плоскости отмечаем точки (1, G 1), (2, G 2), …, (k, Gn), …, (n, Gn), которые последовательно соединяем отрезками прямых. Полученную кривую и называем кривой накопленных частот объекта A (j). Окончательное упорядочение с помощью кривых накопленных частот можно осуществить, пересекая их на каком-либо уровне горизонтальной прямой. Чаще всего выбирают средний уровень Статистический подход исходит из представления, что указанная экспертом ранжировка отклоняется от истинной лишь за счет действия случая. При этом у каждой из ранжировок имеется определенная вероятность оказаться выбранной, т. е. появиться в качестве ответа эксперта. Конечно, эти вероятности различны для различных перестановок. По самому смыслу слова «эксперт» перестановки, более близкие к правильной, должны иметь большую вероятность. Далее, чем лучше, квалифицированнее эксперт, тем распределение вероятностей более сконцентрировано около истинной ранжировки. Плохой или, лучше сказать, «никакой» эксперт с равной вероятностью может назвать любое упорядочение. Такое упорядочение иногда называют чисто случайным. Именно для этого случая вычислены распределения уже упомянутых коэффициентов ранговых корреляций ρ и τ. Представление о том, что отступление от истинной, единственно правильной точки зрения происходят лишь случайно, не всегда согласуется с тем, что мы встречаем на практике. Иногда оказывается, что эксперты делятся на две (а то и более) группы, у каждой из которых свое представление о предмете, свое понятие об истине. В таком случае бессмысленно обрабатывать собранную коллекцию ранжировок как одно целое. Да и сами результаты обработки приобретают неустойчивый характер: небольшие изменения исходного набора, например, исключение нескольких ранжировок или добавление нескольких новых, могут значительно изменить конечный результат (медиану Кемени-Снелла или последовательность средних рангов). Описанная ситуация «нескольких точек зрения» более характерна для опросов общественного мнения, когда по некоторым пунктам нет суждений истинных или ложных, а есть лишь мнения. Вернемся к экспертному ранжированию и статистическому подходу и поговорим о законах распределения вероятностей среди всех n! перестановок. Естественно считать, что правильное упорядочение объектов наиболее вероятно. Соседние с правильным упорядочения имеют вероятности меньшие, но превосходящие вероятности более дальних соседей, и т. д. Возьмем произвольную пару объектов, которые обозначим α и β. Допустим, что в правильной расстановке объект α предшествует объекту β (это, конечно, не означает, что там они стоят рядом). Пусть А - какая-нибудь расстановка объектов, в которой α тоже предшествует β. Поменяем α и β местами, не тронув прочие объекты. Расстановка А перейдет в новую расстановку, которую обозначим В. Что можно сказать о сопутствующем изменении вероятностей? Будем предполагать, что при описанном переходе от А к В вероятность уменьшается. Распределение вероятностей, обладающее этим свойством, будем называть монотонным. Это свойство очень облегчает поиск правильного упорядочения, однако в каждой конкретной экспертизе наличие свойства монотонности представляет собой предположение, которое может оказаться и ложным. Что можно сказать о проверке этого свойства, которая должна бы предшествовать его использованию? Такая проверка неизбежно должна основываться на многократных повторных ранжированиях данного множества объектов одним экспертом, причем ранжирования должны проводиться каждый раз независимо от результатов предшествующих, как бы заново. В практических экспертизах, сделать такое едва ли возможно: раз высказавшись, эксперт не изменит свою точку зрения. Получается, что проводить с одним человеком повторные независимые испытания
|
|||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2020-12-19; просмотров: 322; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.216.229 (0.081 с.) |
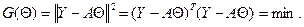
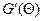 по правилам, обсуждавшимся в разд.6, и приравняем ее нулю:
по правилам, обсуждавшимся в разд.6, и приравняем ее нулю:
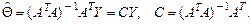 (10.2)
(10.2)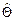 является линейной функцией результатов измерений Y, т.е. случайной величиной. Рассмотрим ее вероятностные характеристики.
является линейной функцией результатов измерений Y, т.е. случайной величиной. Рассмотрим ее вероятностные характеристики.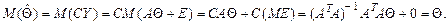
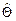 является несмещенной оценкой параметра Θ. Матрица (ATA)-1 является симметричной, поэтому
является несмещенной оценкой параметра Θ. Матрица (ATA)-1 является симметричной, поэтому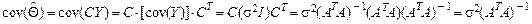 .
.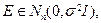 то
то  (10.3)
(10.3)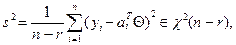 (10.4)
(10.4)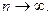
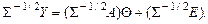 (10.5)
(10.5) = Σ-1/2Σ Σ-1/2 = I.
= Σ-1/2Σ Σ-1/2 = I.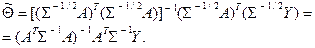
 называют оценкой Гаусса-Маркова. Преобразование, приводящее к модели (5), называется отбеливанием.
называют оценкой Гаусса-Маркова. Преобразование, приводящее к модели (5), называется отбеливанием. -оценка (10.2), полученная на основе измерений y 1,…, yk,
-оценка (10.2), полученная на основе измерений y 1,…, yk, 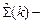 текущая оценка ее ковариационной матрицы в (3), Ak+ 1- (k +1)-я строка матрицы A, соответствующая измерению yk +1. Тогда
текущая оценка ее ковариационной матрицы в (3), Ak+ 1- (k +1)-я строка матрицы A, соответствующая измерению yk +1. Тогда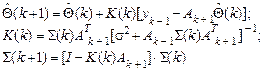 (10.6)
(10.6) 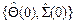 берется произвольный вектор размерности < r ×1> и, например, матрица uI размерности < r × r > с достаточно большим множителем u.
берется произвольный вектор размерности < r ×1> и, например, матрица uI размерности < r × r > с достаточно большим множителем u.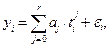
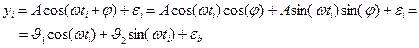
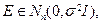

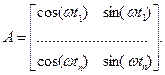
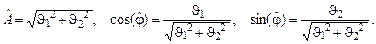
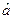 и ее дисперсию, минимизируя сумму квадратов невязок G (a) и получить тот же результат из общей формулы (10.2).
и ее дисперсию, минимизируя сумму квадратов невязок G (a) и получить тот же результат из общей формулы (10.2). на основе явной формулы, полученной в задаче 3 и получить тот же результат из общих соотношений (6).
на основе явной формулы, полученной в задаче 3 и получить тот же результат из общих соотношений (6).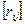 , где ri j — ранг объекта
, где ri j — ранг объекта 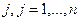 , данный ему экспертом
, данный ему экспертом 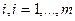 . Строки этой матрицы, представляющие собой перестановки чисел
. Строки этой матрицы, представляющие собой перестановки чисел 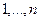 , будем обозначать символами
, будем обозначать символами 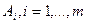 . Задача состоит в том, чтобы по матрице
. Задача состоит в том, чтобы по матрице  . Поэтому главной задачей является определение расстояния между двумя перестановками, скажем, А и В.
. Поэтому главной задачей является определение расстояния между двумя перестановками, скажем, А и В.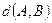 , удовлетворяющая этим свойствам.
, удовлетворяющая этим свойствам.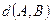 =
= 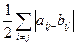 . (11.1)
. (11.1)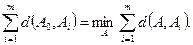
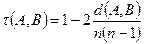 . (11.2)
. (11.2) 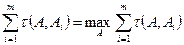
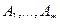 .
. и
и 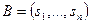 две перестановки целых чисел от 1 до п, то
две перестановки целых чисел от 1 до п, то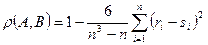 . (11.3)
. (11.3) тоже определенным образом выражает различие между перестановками А и В. Теперь последовательность A0, наиболее коррелированная по Спирмену с набором перестановок
тоже определенным образом выражает различие между перестановками А и В. Теперь последовательность A0, наиболее коррелированная по Спирмену с набором перестановок 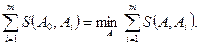
 . (Здесь
. (Здесь 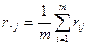 ). Объекты упорядочиваются в соответствии с порядком средних рангов, т. е. первым ставится объект, имеющий наименьший средний ранг, за ним - имеющий второй по величине средний ранг и т. д. Этот способ упорядочения называют «упорядочением по средним рангам». Практически он наиболее употребителен, хотя, прежде, чем применить тот или иной способ обработки, усреднения, полезно убедиться, что собранный статистический материал дает основания для этого действия.
). Объекты упорядочиваются в соответствии с порядком средних рангов, т. е. первым ставится объект, имеющий наименьший средний ранг, за ним - имеющий второй по величине средний ранг и т. д. Этот способ упорядочения называют «упорядочением по средним рангам». Практически он наиболее употребителен, хотя, прежде, чем применить тот или иной способ обработки, усреднения, полезно убедиться, что собранный статистический материал дает основания для этого действия.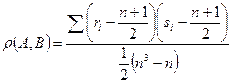 . (11.4)
. (11.4) 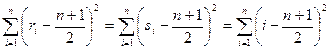 .
.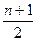 , которую мы вычитаем из рангов ri, si,, есть среднее арифметическое рангов
, которую мы вычитаем из рангов ri, si,, есть среднее арифметическое рангов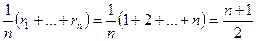 .
.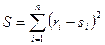 . Отмеченная выше связь между S и ρ позволяет при необходимости использовать эти данные и для расчета распределения ρ.
. Отмеченная выше связь между S и ρ позволяет при необходимости использовать эти данные и для расчета распределения ρ.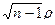 при неограниченном возрастании п стремится к стандартному нормальному. Следовательно, при очень больших п можно пользоваться этой аппроксимацией. Однако при умеренных численностях п нормальная аппроксимация оказывается недостаточной.
при неограниченном возрастании п стремится к стандартному нормальному. Следовательно, при очень больших п можно пользоваться этой аппроксимацией. Однако при умеренных численностях п нормальная аппроксимация оказывается недостаточной.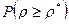 , где ρ *—полученное по наблюденным упорядочениям значение коэффициента Спирмена. Иными словами, вычисляют вероятность получить такое же или большее значение ρ. Малые вероятности этого события указывают на значимость связи между признаками.
, где ρ *—полученное по наблюденным упорядочениям значение коэффициента Спирмена. Иными словами, вычисляют вероятность получить такое же или большее значение ρ. Малые вероятности этого события указывают на значимость связи между признаками.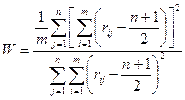 . (11.5)
. (11.5)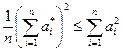 ,
,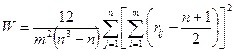 .
. 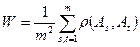 ,
, .
.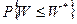 , вычисленная в предположении чистой случайности, то переходить к средним рангам (по всей совокупности) нет оснований. По самому определению W средние ранги в этом случае будут мало различаться между собой. Ранжировка, которую они определят в этом случае, окажется неустойчивой - относительно небольшие изменения в исходном материале могут сильно изменить результат.
, вычисленная в предположении чистой случайности, то переходить к средним рангам (по всей совокупности) нет оснований. По самому определению W средние ранги в этом случае будут мало различаться между собой. Ранжировка, которую они определят в этом случае, окажется неустойчивой - относительно небольшие изменения в исходном материале могут сильно изменить результат.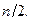 .
.


