Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Лабораторная работа 6. Проверка гипотез согласия
Критерий Колмогорова Этот критерий применяется для проверки простой гипотезы Н 0 о том, что независимые одинаково распределенные случайные величины Х 1, Х 2, …, Хп имеют заданную непрерывную функцию распределения F (x): Найдем функцию эмпирического распределения Fn (x) и будем искать границы двусторонней критической области, определяемой условием А.Н. Колмогоров доказал, что в случае справедливости гипотезы Н 0 распределение статистики Dn не зависит от функции F (x), и при где
- показатель критерия Колмогорова, значения которого можно найти в соответствующих таблицах. Критическое значение критерия λ n (α) вычисляется по заданному уровню значимости α как корень уравнения Можно показать, что приближенное значение вычисляется по формуле где z – корень уравнения На практике для вычисления значения статистики Dn используется то, что
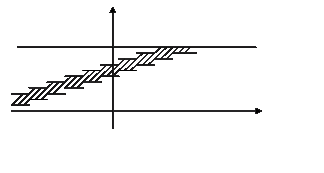
Можно дать следующее геометрическое истолкование критерия Колмогорова: если изобразить на плоскости О ху графики функций Fn (x), Fn (x) ±λ n (α) (рис. 1), то гипотеза Н 0 верна, если график функции F (x) не выходит за пределы области, лежащей между графиками функций Fn (x) -λ n (α) и Fn (x) +λ n (α).
Приближенный метод проверки нормальности распределения, связанный с оценками коэффициентов асимметрии и эксцесса
Определим по аналогии с соответствующими понятиями для теоретического распределения асимметрию и эксцессэмпирического распределения. Асимметрия эмпирического распределения определяется равенством
где т 3 – центральный эмпирический момент третьего порядка. Эксцесс эмпирического распределения определяется равенством
где т 4 – центральный эмпирический момент четвертого порядка. Как известно, для нормально распределенной случайной величины асимметрия и эксцесс равны 0: Задачи
Пример выполнения работы
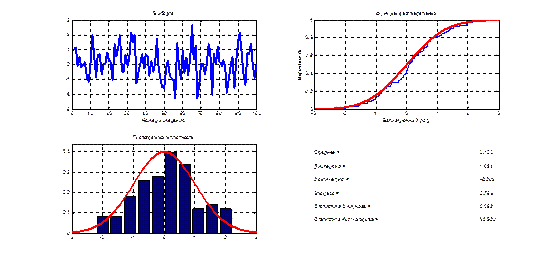
Рис. 6.1. Эмпирическая функция распределения и гипотетическая функция Ф(x, a, s 2) T =0.6828 – гипотеза принимается
Рис. 6.2. Функция распределения Колмогорова (метод Монте-Карло)
Рис. 6.3. Характеристики выборки из нормального закона N (0,1)
|
|||||||||
|
Последнее изменение этой страницы: 2020-12-19; просмотров: 123; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.218.196.182 (0.007 с.) |

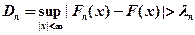 .
. 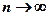
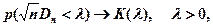
 -
-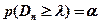 .
. ,
,
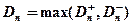 , где
, где 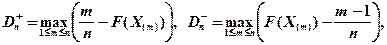
 а
а 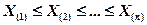 - вариационный ряд, построенный по выборке Х 1, Х 2, …, Хп.
- вариационный ряд, построенный по выборке Х 1, Х 2, …, Хп.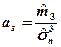 ,
,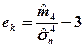 ,
,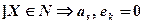 . Поэтому, если соответствующие эмпирические величины достаточно малы, можно предположить, что генеральная совокупность распределена по нормальному закону.
. Поэтому, если соответствующие эмпирические величины достаточно малы, можно предположить, что генеральная совокупность распределена по нормальному закону.