
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Методические указания по выполнению лабораторных работСтр 1 из 9Следующая ⇒
Институт ВОДНОГО ТРАНСПОРТА Кафедра вычислительных систем и информатики А.В. Макшанов
ТЕОРИЯ ИНФОРМАЦИОННЫХ ПРОЦЕССОВ
Методические указания по выполнению лабораторных работ Часть 3
Санкт-Петербург ГУМРФ имени адмирала С. О. Макарова 2020 УДК 514.18 ББК 22.151.3
Рецензент: Доктор технических наук, профессор Марлей В.Е.
Макшанов А. В. Теория информационных процессов и систем. Методические указания по выполнению лабораторных работ. Часть 3. — СПБ.: Изд-во ГУМРФ им. адм. С. О. Макарова, 2017. — 90 с.
Рассмотрены основные приемы интеллектуального анализа данных, интегрированные в лабораторный практикум. В качестве инструментальной среды разработки используется математическая система MatLab версий 6.5 и выше. Методические указания предназначены для формирования у студентов академического и прикладного бакалавриатов по направлению 09.03.02 «Информационные системы и технологии» компетенций в соответствии с рабочей программой дисциплины «Теория информационных процессов и систем». Методические указания также могут быть использовано студентами, магистрантами и аспирантами других инженерно–технических специальностей, желающими самостоятельно изучить вопросы анализа экспериментальных данных. Рекомендовано к изданию в качестве методических указаний по выполнению лабораторных работ по направлению подготовки 09.03.02 «Информационные системы и технологии» заседанием кафедры вычислительных систем и информатики от 30.08.2020, протокол № 5.
Оглавление
Введение В теории вероятностей строится модель, позволяющая определить вероятности некоторых относительно простых событий и рассчитать на их основе вероятности более сложных событий. Ожидается, что найденные вероятности можно интерпретировать как относительные частоты и, тем самым, предсказать частоты появления этих сложных событий.
Математическая статистика – это обратная задача теории вероятностей. В ней заданы те самые частоты, полученные в результате наблюдений, и требуется объяснить эти частоты на основе возможно более простого вероятностного механизма. Эта задача является некорректной, поскольку полученные наблюдения можно объяснить в рамках различных моделей. Чтобы выбрать единственную модель, приходится использовать доступную априорную информацию, заданную в различных формах. В зависимости от формы этой априорной информации статистику разделяют на параметрическую, непараметрическую и робастную. Основное предположение математической статистики состоит в том, что наблюдения представлены в числовой форме и представляют собой независимые измерения одной и той же величины в неизменных условиях. На языке теории вероятностей это означает, что имеются результаты n экспериментов - числа x 1,…, xn, которые являются независимыми реализациями случайной величины X с некоторой функцией распределения F (x). На практике x 1,…, xn – это числа. Для теоретических расчетов считают, что каждое измерение xi – это случайная величина с функцией распределения F (x). Разницу между этими подходами можно прояснить на примере бросания монеты. Если мы бросаем монету n раз в одних и тех же условиях, мы получаем последовательность чисел, нулей и единиц (ноль –«орел», единица – «решка»). Однако можно сразу бросить n монет, тогда результат для i -й монеты – это случайная величина: 0 с вероятностью p, 1 с вероятностью q =1- p. Параметр p зависит от характеристик монеты и используемого способа бросания, при простейшей организации процесса бросания p =1/2. Кратко это предположение выражают так: x 1,…, xn образуют выборку с теоретическим законом распределения F (x) или x 1,…, xn образуют выборку из распределения F (x). Основная задача математической статистики состоит в том, чтобы предложить вероятностный механизм, породивший именно данные значения x 1,…, xn, т.е. оценить теоретический закон F (x). Оценка любого параметра теоретического распределения на практике выступает как конкретное число, а в теории – как случайная величина, функция от выборочных значений – случайных величин x 1,…, xn. Любая такая функция называется статистикой, для нее можно изучать ее закон распределения, а также ее среднее, дисперсию и т.д.
Если мы говорим, что x 1,…, xn – выборка, то тем самым мы уже принимаем некоторую вероятностную модель для результатов наблюдения. В частности, если распределение F предполагается непрерывным, мы объявляем, что имеет смысл рассматривать вероятности
где Для удобства вычислений выборочные значения обычно упорядочивают по возрастанию и получают так называемый вариационный ряд
Члены вариационного ряда называют порядковыми статистиками. В частности, широко используется выборочная медиана – оценка медианы теоретического распределения
и выборочный размах x ( n ) - x (1). Основной, до сих пор актуальный принцип получения статистических оценок предложил в 1909 г. немецкий философ Карл Пирсон. Он предложил вводить фиктивную, «эмпирическую» случайную величину x *, принимающую значения x 1,…, xn с вероятностью 1/ n. Если нужно оценить некую характеристику теоретического закона распределения, то в качестве оценки предлагается использовать такую же характеристику величины x *. Например, оценкой математического ожидания a теоретического распределения является математическое ожидание x *, т.е. выборочное среднее
Аналогично, оценкой теоретической дисперсии является выборочная дисперсия
а оценкой самой теоретической функции распределения F (x) – эмпирическая функция распределения F* (x), т.е. функция распределения x *. F* (x) – это ступенчатая функция, возрастающая от 0 до 1 и имеющая в каждой точке xi скачок, равный 1/ n. Это – самые простые оценки. В действительности использование такой оценки для момента порядка k связано с допущением, что теоретическое распределение имеет конечные моменты до порядка 2 k. При наличии дополнительной информации о F (x) можно получать оценки более высокого качества. Пример выполнения работы
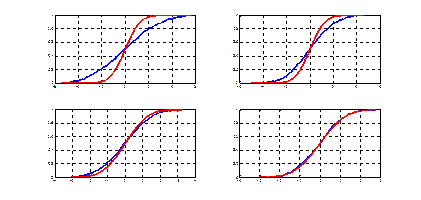
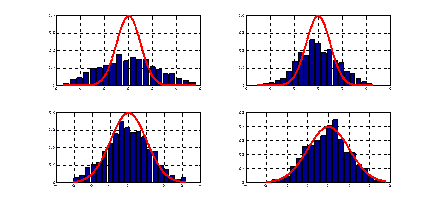
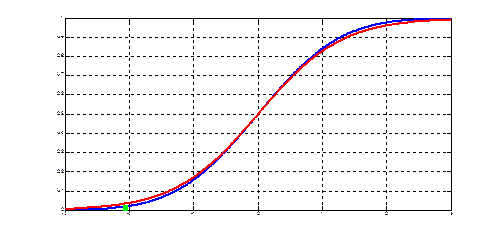
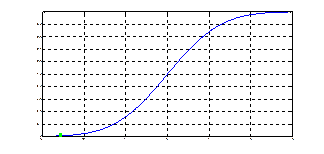
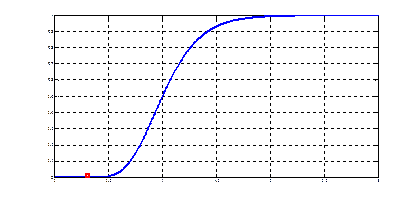
Рис. 1.1. Сходимость по распределению к нормальному закону
Рис. 1.2. Сходимость оценок плотности к плотности нормального закона
Пример выполнения работы
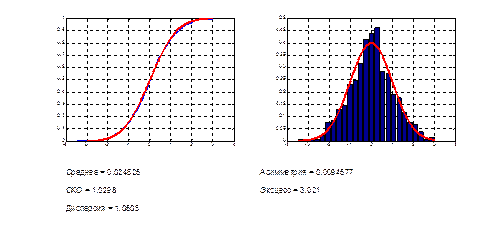
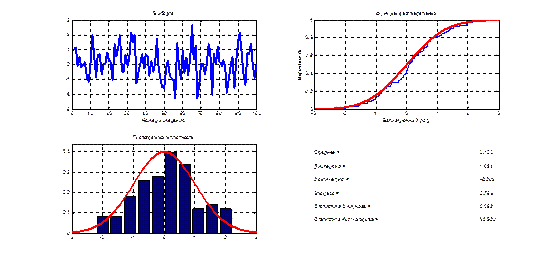
Рис. 2.1. Оценивание основных характеристик случайной выборки
Пример выполнения работы
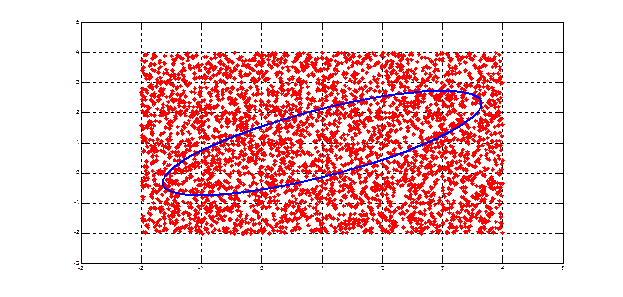
Экранный вывод (N =4000): Площадь эллипса и его оценка [ 9.4248 9.4320 ] Рис. 3.1. Вычисление площади эллипса по методу Монте-Карло
Пример выполнения работы
Рис.4.1. Доверительный интервал для среднего
Рис.4.2. Доверительный интервал для дисперсии
Рис.4.3. Теоретическая и эмпирическая функции распределения закона хи-квадрат
Задачи
Пример выполнения работы
Рис.5.1. Проверка гипотезы о среднем. Односторонняя гипотеза отвергается с надежностью порядка 0.98
Рис.5.2. Проверка гипотезы о равенстве средних. Двусторонняя гипотеза отвергается с надёжностью 0.98
Рис.5.3. Проверка гипотезы о равенстве дисперсий. Двусторонняя гипотеза отвергается с надёжностью 0.98
Критерий Колмогорова Этот критерий применяется для проверки простой гипотезы Н 0 о том, что независимые одинаково распределенные случайные величины Х 1, Х 2, …, Хп имеют заданную непрерывную функцию распределения F (x): Найдем функцию эмпирического распределения Fn (x) и будем искать границы двусторонней критической области, определяемой условием А.Н. Колмогоров доказал, что в случае справедливости гипотезы Н 0 распределение статистики Dn не зависит от функции F (x), и при где
- показатель критерия Колмогорова, значения которого можно найти в соответствующих таблицах. Критическое значение критерия λ n (α) вычисляется по заданному уровню значимости α как корень уравнения Можно показать, что приближенное значение вычисляется по формуле где z – корень уравнения На практике для вычисления значения статистики Dn используется то, что
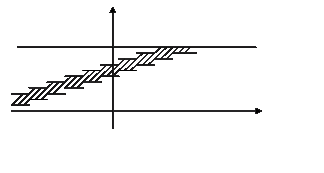
Можно дать следующее геометрическое истолкование критерия Колмогорова: если изобразить на плоскости О ху графики функций Fn (x), Fn (x) ±λ n (α) (рис. 1), то гипотеза Н 0 верна, если график функции F (x) не выходит за пределы области, лежащей между графиками функций Fn (x) -λ n (α) и Fn (x) +λ n (α).
Задачи
Пример выполнения работы
Рис. 6.1. Эмпирическая функция распределения и гипотетическая функция Ф(x, a, s 2) T =0.6828 – гипотеза принимается
Рис. 6.2. Функция распределения Колмогорова (метод Монте-Карло)
Рис. 6.3. Характеристики выборки из нормального закона N (0,1) Шкалы измерений
В математическом смысле шкалой называют правило, по которому состояния системы характеризуются числами. Итак, шкала — это переход от физического (или другого) объекта к числу. В данном смысле шкалой будет любая календарная система - моменту времени приписывается определенная дата. Шкалу представляет собой и принятая в школе система оценок, выставляемых ученикам в зависимости отих успехов. Упомянутые шкалы - длин, температур, времени, успехов — различаются не только по содержанию. Между ними есть и важные формальные различия. Результатом измерения в любой шкале является число. С числами можно проводить арифметические и другие операции. Результаты некоторых операций имеют содержательный смысл и истолковываются в рамках данной шкалы. Допустим, чтомы измеряем длины предметов. Если х и у - длины отрезков а и b, то х + у - длина отрезка, полученного приставлением а к b, Если же х и у — две календарные даты, причем х > у, то х – у имеет смысл - это время, прошедшее от одного события до другого. Однако х + у, ху, х/у и т. п. содержательного смысла лишены. Для показателей по шкале успехов еще меньше осмысленных соотношений: осмысленно их можно лишь сравнивать по величине, т. е. из соотношения отметок х < у для учеников а и b можно лишь заключить, что а учится хуже, чем b. Если же у - х = 1, то утверждение «успехи b на 1 выше, чем успехи а» не объясняет, каково различие между ними. Шкала успехов служит примером порядковой (ранговой) шкалы. Выделяют еще номинальную шкалу, где числа служат всего лишь для различения отдельных возможностей, как бы для их названия. Никаких содержательных соотношений, кроме х = у и х Если x 1,…, xn – действительно числа, результаты измерений, то среди них могут содержаться грубые промахи, аномальные измерения. Даже одно такое аномальное значение может увести далеко в сторону большинство статистик – как оценок, так и статистик критериев (критериальных функций). В то же время, на ранговую структуру выборки оно окажет минимальное воздействие. Ранговые методы всегда ориентируются на основное ядро выборки и мало чувствительны к далеко выпадающим значениям. Если Ранговые методы. Критерий Вилкоксона и медиана Ходжеса-Леман а
Пусть Для проверки гипотезы однородности наиболее известен критерий Стьюдента, основанный на сравнении средних значений обеих выборок. Для того, чтобы получаемые на его основе выводы были справедливы, нужно, чтобы обе выборки имели близкое к гауссовому распределение с одной и той же дисперсией. Можно применять для проверки Н и критерий Смирнова, основанный на разности эмпирических функций распределения, построенных по каждой выборке отдельно. Критерий Смирнова - чисто непараметрический. Для того, чтобы он был применим, необходима лишь непрерывность истинных функций распределения F и G. Более того, вероятность того, что различие между F и G будет замечено, если оно вообще существует, растет и приближается к 1 при неограниченном увеличении объемов выборок т и п. К сожалению, скорость роста этой вероятности невелика, так что при умеренных значениях т и п мощность критерия Смирнова мала. Мы хотим применить критерии, основанные на рангах. Для этого объединяем обе выборки в одну группу и ранжируем наблюдения. Достаточно знать ранги только игреков, поскольку ранги иксов можно по ним восстановить - это оставшиеся числа из последовательности 1, 2,..., m + n. Обозначим ранги игреков через Легко понять, что при справедливости гипотезы Н в качестве рангов Остается выбрать подходящую функцию рангов, на которой основывать проверку H. Для этого, как всегда, надо подумать о конкурирующих гипотезах, т.е. о том, каким образом может нарушаться H. Рассмотрим наиболее удобную для ранговых методов возможность: нарушение равенства F= G в пользу F< G. Таким соотношение между F и G будет, в частности, в том случае, когда G является «сдвигом» F, т. е. при Пример. Сравниваются длительности плавки в мартеновской печи при работе по стандартной и усовершенствованной технологиям. Естественно считать, что Мы надеемся, что сокращение длительности плавки действительно происходит. Используем обычный логический прием - рассуждение от противного. Предположим, что θ=0, т. е. F = G. Если статистический материал заставит нас отвергнуть это предложение, придется признать, что θ в самом деле положительно. Надо, следовательно, проверить гипотезу H против альтернативы F< G. Если G действительно превосходит F, т. е. если P (xi < x) < P (yi < x), то элементы выборки {1, 2,..., т + п }. Поэтому статистика Это правило было предложено в 1945 году и послужило отправной точкой для всей обширной области ранговых процедур. По имени ее автора статистика W = r1+…+ rn называется статистикой Вилкоксона, а основанный на W критерий - критерием Вилкоксона. Мы выяснили, каково должно быть поведение W при F< G . Поэтому мы отвергнем H, если W окажется меньше критического значения Wкрит или равным ему. Это критическое значение выбираем так, чтобы Если конкурентом однородности служит возможность F> G, признаком нарушения Н служит слишком большая величина W. Часто применяют двусторонний критерий Вилкоксона, по которому гипотеза Н отвергается, если наблюденное значение выходит за критические значения Значение α подбирают так, чтобы Исследования показали, что мощность критерия Вилкоксона против рассмотренных здесь альтернатив намного превосходит мощность критерия Смирнова. Однако против многих других альтернатив критерий W бессилен, в то время как критерий Смирнова обнаруживает (при неограниченных объемах выборок) любое различие. Легко увидеть, что в объединенной выборке сумма всех рангов равна
так что на каждое из (m + n) измерений приходится «средний ранг» (m + n+ 1)/2. Мы следим за положением
Дисперсия статистики W вычисляется несколько сложнее:
При достаточно больших m, n (больше 20) распределение W хорошо аппроксимируется нормальным законом:
при меньших m, n есть специальные таблицы. Составить представление о возможностях W можно, рассмотрев какие-либо конкретные F и G. Пусть
Задачи
Пример выполнения работы
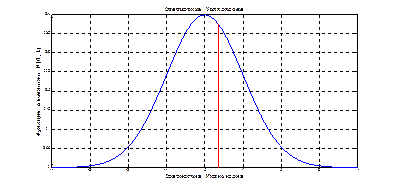
Рис.7.1. Статистика критерия Уилкоксона и её гауссова аппроксимация
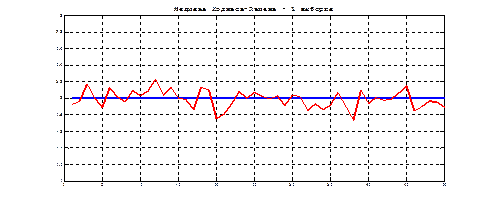
Рис.7.2. Медиана Ходжеса-Лемана – 50 имитаций
Задачи
Пример выполнения работы
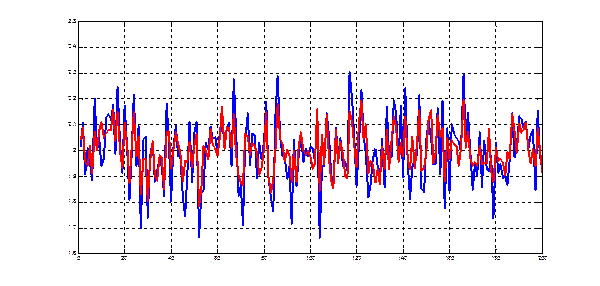
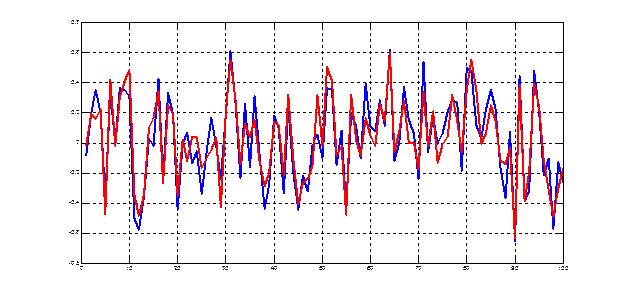
Рис.8.1. Прогноз второй (ненаблюдаемой) компоненты по первой (наблюдаемой)
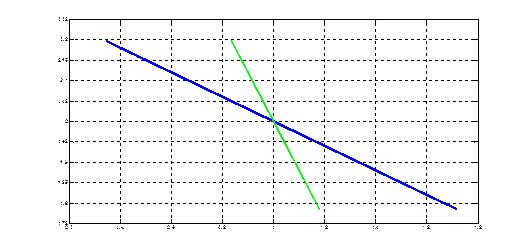
Рис.8.2. Прямые среднеквадратической регрессии компонент друг на друга Задачи
Пример выполнения работы
Рис.9.1. Прогноз третьей (ненаблюдаемой) компоненты по первым двум (наблюдаемым)
В ЛИНЕЙНОЙ МОДЕЛИ ИЗМЕРЕНИЙ Предположим, что вектор результатов измерений Y =[ y 1,…, yn ] T имеет следующую структуру: Y = A Θ+ E, (10.1) где Θ = [ θ 1,…, θr ] T – вектор неизвестных, но вполне определенных параметров, подлежащий оцениванию; A = [ aij ] – известная матрица размерности n × r, r ≤ n, имеющая максимально возможный ранг r; E =[ ε 1,…, εn ] T – вектор случайных погрешностей измерений. Предположим, что компоненты вектора E – независимые случайные величины со средним 0 и дисперсией σ 2: ME =0, cov(E)= σ 2 I, где I – единичная матрица. Такая схема связи результатов измерений (откликов) и неизвестных параметров (факторов) называется линейной моделью измерений. Будем искать оценку вектора Θ из условия
Такой подход к оцениванию неизвестных параметров называется методом наименьших квадратов (МНК). Найдем производную
откуда
Оценка
Таким образом,
Если вектор случайных погрешностей измерений E является гауссовым,
Если дисперсия σ2 неизвестна, то можно использовать ее несмещенную оценку
которая в гауссовом случае оказывается независимой от В гауссовом случае оценка по МНК является оценкой максимального правдоподобия и, тем самым, обладает целым рядом важнейших свойств эффективности. В негауссовых ситуациях при весьма общих предположениях о законе распределения погрешностей измерений она остается эффективной в классе оценок, линейных по y 1,…, yn, но, например, соотношение (10.3) выполняется лишь асимптотически при
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2020-12-19; просмотров: 87; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.17.110.58 (0.17 с.) |
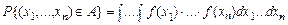 ,
,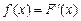 - теоретическая плотность. Иными словами, мы объявляем, что в принципе совокупность из n наблюдений может быть повторена сколько угодно раз, причем n –мерный вектор, получающийся при каждом повторении n наблюдений, будет попадать в множество A с частотой, примерно равной найденной
- теоретическая плотность. Иными словами, мы объявляем, что в принципе совокупность из n наблюдений может быть повторена сколько угодно раз, причем n –мерный вектор, получающийся при каждом повторении n наблюдений, будет попадать в множество A с частотой, примерно равной найденной 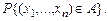
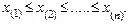
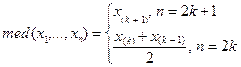
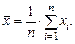
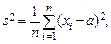



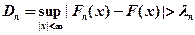 .
. 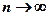
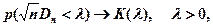
 -
-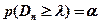 .
. ,
,
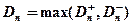 , где
, где 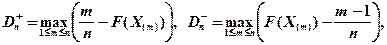
 а
а 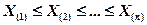 - вариационный ряд, построенный по выборке Х 1, Х 2, …, Хп.
- вариационный ряд, построенный по выборке Х 1, Х 2, …, Хп.

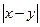 — разница длин отрезков, ху — площадь прямоугольника, образованного этими отрезками, и т. п. Однако ху или, например, log(x)для нас не имеют содержательного толкования.
— разница длин отрезков, ху — площадь прямоугольника, образованного этими отрезками, и т. п. Однако ху или, например, log(x)для нас не имеют содержательного толкования.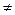 у, между такими числами нет. Конечно, выбор чисел (т. е. номинальной шкалы) вместо реальных имен или других способов идентификации не обязателен, более того, может привести к недоразумениям.
у, между такими числами нет. Конечно, выбор чисел (т. е. номинальной шкалы) вместо реальных имен или других способов идентификации не обязателен, более того, может привести к недоразумениям.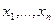 - измерения в порядковой шкале, то сами их значения смысла не имеют, важен только их порядок, т.е. их ранговая структура. В номинальной шкале числовой смысл имеют только численности групп.
- измерения в порядковой шкале, то сами их значения смысла не имеют, важен только их порядок, т.е. их ранговая структура. В номинальной шкале числовой смысл имеют только численности групп.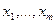 и
и 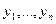 - две независимые выборки. Неизвестные законы распределения случайных величин
- две независимые выборки. Неизвестные законы распределения случайных величин 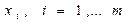 и
и 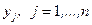 обозначим через
обозначим через 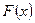 и
и 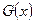 соответственно. По данным наблюдениям хотим проверить гипотезу однородности H:
соответственно. По данным наблюдениям хотим проверить гипотезу однородности H: 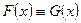 .
.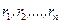 . Статистика для проверки Н должна быть функцией этих чисел.
. Статистика для проверки Н должна быть функцией этих чисел.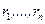 с равными вероятностями могут появляться любые п чисел из 1, 2,..., т + п. Это дает возможность рассчитать при выполнении H закон распределения любой статистики, основанной на рангах. Это обстоятельство — основная причина перехода к рангам, причина универсальности и простоты ранговых методов.
с равными вероятностями могут появляться любые п чисел из 1, 2,..., т + п. Это дает возможность рассчитать при выполнении H закон распределения любой статистики, основанной на рангах. Это обстоятельство — основная причина перехода к рангам, причина универсальности и простоты ранговых методов.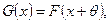
 . Такие альтернативы реально возникают в некоторых задачах, например, при измерении какой-то величину, обладающей естественной изменчивостью, при различных управляющих воздействиях.
. Такие альтернативы реально возникают в некоторых задачах, например, при измерении какой-то величину, обладающей естественной изменчивостью, при различных управляющих воздействиях.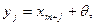 где
где 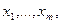
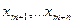 последовательность независимых одинаково распределенных случайных величин, θ - закономерное изменение (сокращение, если θ<0) длительности плавки. Конечно, величина θ не наблюдается. Наблюдаются выборки
последовательность независимых одинаково распределенных случайных величин, θ - закономерное изменение (сокращение, если θ<0) длительности плавки. Конечно, величина θ не наблюдается. Наблюдаются выборки 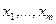 и
и  (Если θ>0, альтернативой к H служит F> G).
(Если θ>0, альтернативой к H служит F> G).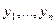 имеют тенденцию располагаться левее элементов выборки
имеют тенденцию располагаться левее элементов выборки 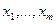 . Это значит, что ранги игреков имеют тенденцию располагаться в левой части последовательности
. Это значит, что ранги игреков имеют тенденцию располагаться в левой части последовательности в случае F< G склонна к меньшим значениям, нежели в случае F= G. Из этого следует статистическое правило: отвергать гипотезу F= G (в пользу F < G), если r1 + … rn слишком мала.
в случае F< G склонна к меньшим значениям, нежели в случае F= G. Из этого следует статистическое правило: отвергать гипотезу F= G (в пользу F < G), если r1 + … rn слишком мала.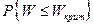 при H была малой.
при H была малой.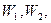 т. е. если не происходит событие
т. е. если не происходит событие 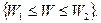 Критические значения
Критические значения  находят по таблицам из условия
находят по таблицам из условия
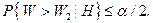
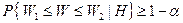 была достаточно близка к 1.
была достаточно близка к 1.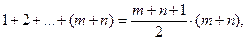
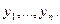 Если гипотеза H верна, то они распределены в объединенной выборке приблизительно равномерно, так что на их сумму приходится в среднем величина
Если гипотеза H верна, то они распределены в объединенной выборке приблизительно равномерно, так что на их сумму приходится в среднем величина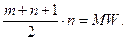
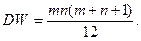
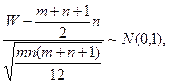
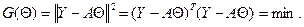
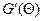 по правилам, обсуждавшимся в разд.6, и приравняем ее нулю:
по правилам, обсуждавшимся в разд.6, и приравняем ее нулю:
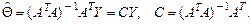 (10.2)
(10.2)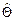 является линейной функцией результатов измерений Y, т.е. случайной величиной. Рассмотрим ее вероятностные характеристики.
является линейной функцией результатов измерений Y, т.е. случайной величиной. Рассмотрим ее вероятностные характеристики.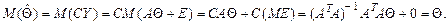
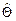 является несмещенной оценкой параметра Θ. Матрица (ATA)-1 является симметричной, поэтому
является несмещенной оценкой параметра Θ. Матрица (ATA)-1 является симметричной, поэтому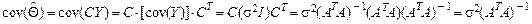 .
.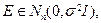 то
то  (10.3)
(10.3)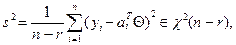 (10.4)
(10.4)


