
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Апостериорные вероятность и плотность вероятности параметра радиосигнала
В соответствии со сформулированным выше байесовским подходом к проектированию оптимальных РСПИ для решения задач оптимального приёма радиосигналов необходимо вычислять апостериорную вероятность или плотность вероятности параметра радиосигнала. Наиболее общей задачей оптимального радиоприёма является задача фильтрации. В достаточно общем виде задачу фильтрации можно сформулировать так. Пусть непосредственному наблюдению на текущем интервале времени [0,T] доступны реализации сл.пр.
Полезный сигнал Предположим пока, что известны следующие априорные сведения относительно наблюдаемого процесса 1) известен конкретный вид детерминированной функции F(•), т.е. способ комбинирования сигнала и помехи; 2) сигнал 3) известны все необходимые вероятностные характеристики сл.пр. Располагая этими априорными сведениями, а также доступной непосредственному наблюдению реализацией процесса Вначале рассмотрим уравнения (алгоритм) фильтрации в дискретном времени: Исходной для получения уравнения фильтрации является формула Байеса. Запишем один из вариантов этой формулы применительно к уравнениям наблюдения
и динамики сообщения
где Уравнение динамики сообщения в дискретном времени является аналогом уравнения
являющегося математической моделью передаваемого сообщения λ(t) в непрерывном времени (см. 1.2.1. Статистические модели и характеристики непрерывных сообщений). Допустим, что апостериорная плотность вероятности (АПВ) Зная АПВ, можно найти оценку, оптимальную по любому критерию. Например, вычисленное по формуле
апостериорное м.о. определит алгоритм формирования оценки
- точность полученной оценки. На основании правила умножения вероятностей для условной ПВ
Поскольку в уравнении наблюдения полезный сигнал
Учитывая, что совокупность случайных величин
В результате получаем
Значения процесса λ в ПВ
Уравнение (3) является основным уравнением фильтрации в дискретном времени. Его можно рассматривать как вариант формулы Байеса. Вспомним, что формула Байеса определяет АПВ через произведение трёх сомножителей: 1 – нормировочная константа, 2 – априорная ПВ, 3 – функция правдоподобия. В полученном варианте формулы Байеса второй сомножитель представляет собой условную ПВ
Эта формула получается на основании условия согласованности плотностей вероятности и правила умножения вероятностей
где В правой части выражения (4) АПВ
Третий сомножитель в полученном варианте (3) формулы Байеса - условная ПВ Формулы (3), (4) при известном начальном распределении Получим алгоритм фильтрации для случая, когда уравнения наблюдения и динамики заданы в непрерывном времени:
Такое уравнение является обобщением уравнения
Случайные процессы
где Оператор ФПК имеет следующий вид
Коэффициенты
Коэффициент сноса Рассмотрим гауссовско-марковский экспоненциально-коррелированный сл.пр.
где Формальное решение уравнения имеет вид
Сл.пр.
где м.о.
Коэффициенты сноса и диффузии:
Уравнение ФПК:
Фундаментальное решение этого уравнения при детерминированном начальном условии Характер изменения п.в. перехода
Рис. 2.6. Изменение плотности вероятности перехода во времени
Начальная дельтообразная п.в.
В случае непрерывного времени уравнение для апостериорной плотности вероятности удобно получить из полученного выше уравнения фильтрации в дискретном времени путем предельного перехода. Перепишем уравнение (3) иначе, введя явную зависимость от времени
где Распишем два сомножителя, входящих в правую часть этого уравнения. При этом применительно к уравнениям наблюдения и динамики сообщения будем использовать процедуру дискретизации
Так как
где С использованием оператора ФПК и функции
где АПВ
Представленное стохастическое интегродифференциальное уравнение фильтрации в непрерывном времени называется уравнением Стратоновича. В качестве начального условия для его решения берется априорная ПВ
В правую часть уравнения Стратоновича непосредственно входят априорные сведения об оцениваемом процессе Уравнение Стратоновича при фильтрации в непрерывном времени полностью описывает эволюцию АПВ фильтруемого параметра. Качественный характер изменения АПВ
Рис. 2.7. Эволюция АПВ
Точное решение уравнения Стратоновича можно получить для задачи оценки сообщения, представляющего собой случайную величину. Задача оценки сл.в. является частным случаем задачи оптимальной фильтрации случайных процессов. Пусть по наблюдению
требуется получить оптимальную оценку параметра λ, представляющего собой случайную величину с известной априорной плотностью вероятности
следовательно
Проинтегрируем по времени обе части этого уравнения с учётом того, что F(t) не зависит от
Следовательно, АПВ получается в виде
Запишем это уравнение в соответствии с формулой Байеса
откуда следует, что функционал правдоподобия реализации
Значит функция Прологарифмировав уравнение для АПВ, получим алгоритм нахождения оценки по максимуму АПВ:
Во многих практических задачах априорная ПВ является очень «широкой» и не оказывает существенного влияния на положение максимума АПВ. При этом оценка по максимуму АПВ (ее логарифма) практически совпадает с оценкой по максимуму функционала правдоподобия (его логарифма):
где Корреляционный интеграл ещё называют взаимокорреляционной функцией между принимаемым колебанием и полезным сигналом. Если оцениваются неэнергетические параметры сигнала (параметры, от которых энергия сигнала не зависит), то их оценку можно находить по максимуму корреляционного интеграла
Этот алгоритм нашел широкое применение на практике в РСПИ, он реализуется с помощью корреляторов и согласованных фильтров.
Корреляторы
Мы установили, что для получения оптимальной оценки сообщения необходимо вычислять корреляционный интеграл. Подтвердим этот вывод на примере задачи обнаружения сигнала. Эта задача встречается в двоичных системах передачи информации с пассивной паузой. Пусть в принятом колебании
Здесь Рассмотрим наиболее простой случай – обнаружение детерминированного сигнала. В детерминированном сигнале Для задачи обнаружения детерминированного сигнала по аналогии с задачей оценки непрерывного сообщения l запишем апостериорную вероятность того, что дискретный параметр
Решение о наличии или отсутствии сигнала на интервале наблюдения принимается в результате сравнения отношения апостериорных вероятностей в конце интервала наблюдения Т с некоторым порогом:
Если априорные вероятности значений дискретного параметра Алгоритм работы обнаружителя можно упростить. Будем считать энергию сигнала фиксированной (сигнал полностью расположен внутри интервала наблюдения)
Учитывая монотонное поведение показательной функции и прологарифмировав, получим окончательный алгоритм работы оптимального обнаружителя
Выходной сигнал q(t) можно представить в виде суммы сигнальной qs(t) и шумовой qn(t) составляющих:
Функция qs(t) представляет собой выходной полезный сигнал на выходе приемника-обнаружителя, а функция qn(t) — выходной шум. Существенное различие между ними состоит в том, что первая является детерминированной, а вторая — случайной, разной для разных реализации наблюдения. Отношение пикового значения сигнальной функции qs(t) к среднеквадратическому значению шумовой функции qn(t) равно Алгоритм обнаружения можно реализовать с использованием коррелятора или согласованного фильтра с импульсной характеристикой вида Специально укажем, что назначение оптимальных приемников обнаружения состоит не в наилучшем воспроизведении входного полезного сигнала, а в формировании наибольшего пикового отношения сигнал-шум в момент времени t=T и сравнении выходного сигнала в этот момент времени с некоторым порогом h. Из представленных структурных схем (рис. 2.8) видно, что коррелятор – это устройство, непосредственно реализующее алгоритм нахождения корреляционного интеграла.
Рис. 2.8. Структурные схемы оптимальных обнаружителей: а) детерминированного сигнала с использованием коррелятора б) согласованного фильтра
Согласованный фильтр реализует алгоритм нахождения корреляционного интеграла в неявном виде.
|
|||||||||
|
Последнее изменение этой страницы: 2020-11-11; просмотров: 404; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.120.109 (0.066 с.) |
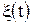 , являющиеся детерминированной функцией от полезного сигнала
, являющиеся детерминированной функцией от полезного сигнала 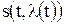 и помехи n(t):
и помехи n(t):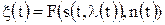 .
.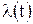 , представляющего собой непрерывный сл.пр.
, представляющего собой непрерывный сл.пр.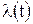 и помехи n(t). Априорные сведения о
и помехи n(t). Априорные сведения о 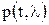 непрерывного сообщения
непрерывного сообщения 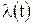 , позволяющую получить его текущую оценку
, позволяющую получить его текущую оценку 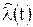 по любому критерию.
по любому критерию.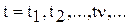 , где
, где 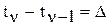 .
.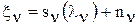 ,
, 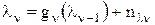
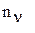 - ДБГШ - дискретный белый (значения в различные моменты времени независимы) гауссовский (значения распределены по нормальному закону) шум наблюдения (помеха) с нулевым м.о. и дисперсией, равной
- ДБГШ - дискретный белый (значения в различные моменты времени независимы) гауссовский (значения распределены по нормальному закону) шум наблюдения (помеха) с нулевым м.о. и дисперсией, равной 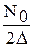 , где
, где 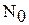 – спектральная плотность мощности соответствующего непрерывного БГШ n(t);
– спектральная плотность мощности соответствующего непрерывного БГШ n(t); 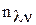 - формирующий (информационный) ДБГШ.
- формирующий (информационный) ДБГШ.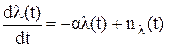 ,
,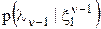 для момента времени
для момента времени 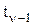 найдена. Необходимо найти плотность
найдена. Необходимо найти плотность 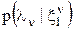 для следующего момента времени
для следующего момента времени 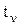 .
.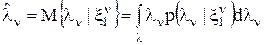 (1)
(1)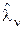 , оптимальной по критерию минимума среднего квадрата ошибки, а апостериорная дисперсия
, оптимальной по критерию минимума среднего квадрата ошибки, а апостериорная дисперсия 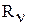 , являющаяся минимальным значением апостериорного риска,
, являющаяся минимальным значением апостериорного риска,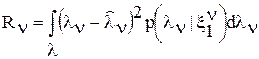 (2)
(2)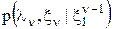 можно записать выражение
можно записать выражение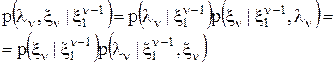
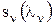 является детерминированной функцией аргументов, а
является детерминированной функцией аргументов, а 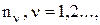 - последовательность независимых случайных величин, то величина
- последовательность независимых случайных величин, то величина  при фиксированном
при фиксированном 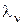 зависит только от
зависит только от  и не зависит от предыдущих значений ДБГШ. Поэтому
и не зависит от предыдущих значений ДБГШ. Поэтому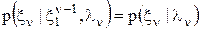
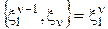 , можно записать
, можно записать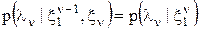

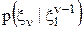 не входят, и поэтому сомножитель 1/
не входят, и поэтому сомножитель 1/ 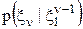 можно учесть в АПВ с помощью нормировочной константы С:
можно учесть в АПВ с помощью нормировочной константы С: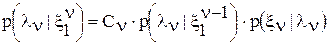 (3)
(3)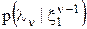 экстраполированного (прогнозируемого) значения
экстраполированного (прогнозируемого) значения 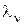 в отсутствие отсчета
в отсутствие отсчета 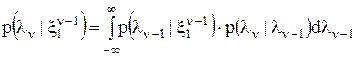 (4).
(4).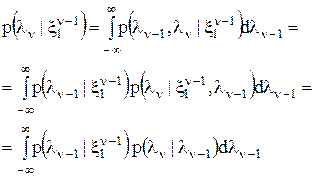
 вследствие того, что при известном значении
вследствие того, что при известном значении 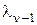 значение
значение 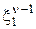 не добавляет сведений о
не добавляет сведений о 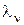 .
.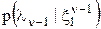 предполагается известной, а условная ПВ
предполагается известной, а условная ПВ 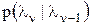 может быть найдена из уравнения динамики сообщения.
может быть найдена из уравнения динамики сообщения.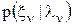 - представляет собой текущее значение функции правдоподобия и находится из уравнения наблюдения. Для этого в нормальной ПВ
- представляет собой текущее значение функции правдоподобия и находится из уравнения наблюдения. Для этого в нормальной ПВ 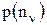 нужно перейти к новой переменной
нужно перейти к новой переменной 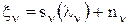 .
.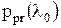 позволяют рекуррентно вычислять АПВ фильтруемого параметра и совместно с формулой (1) для оценки
позволяют рекуррентно вычислять АПВ фильтруемого параметра и совместно с формулой (1) для оценки 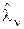 дают оптимальный алгоритм, полностью решающий задачу фильтрации в дискретном времени. Точность фильтрации характеризуется значением апостериорной дисперсии (2).
дают оптимальный алгоритм, полностью решающий задачу фильтрации в дискретном времени. Точность фильтрации характеризуется значением апостериорной дисперсии (2).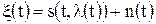
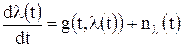
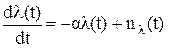
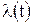 , заданные подобными уравнениями, относятся к классу так называемых диффузионных марковских процессов. Априорная динамика плотности вероятности такого процесса определяется дифференциальным уравнением в частных производных Фоккера-Планка-Колмогорова (ФПК), которое имеет вид
, заданные подобными уравнениями, относятся к классу так называемых диффузионных марковских процессов. Априорная динамика плотности вероятности такого процесса определяется дифференциальным уравнением в частных производных Фоккера-Планка-Колмогорова (ФПК), которое имеет вид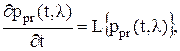
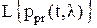 - оператор ФПК.
- оператор ФПК.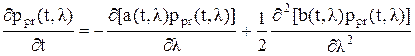 .
. 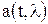 и
и 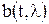 , называются коэффициентами сноса и диффузии (по традиции, связанной с применением уравнения ФПК первоначально для изучения поведения броуновских частиц) и определяются из соотношений:
, называются коэффициентами сноса и диффузии (по традиции, связанной с применением уравнения ФПК первоначально для изучения поведения броуновских частиц) и определяются из соотношений: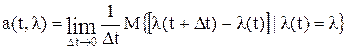 ,
, 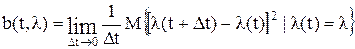 .
. 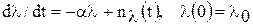 ,
,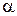 - постоянный коэффициент,
- постоянный коэффициент, 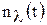 - БГШ со спектральной плотностью
- БГШ со спектральной плотностью 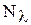 . Такой процесс формируется на выходе интегрирующей RC-цепочки при подаче на вход БГШ.
. Такой процесс формируется на выходе интегрирующей RC-цепочки при подаче на вход БГШ.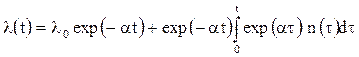 .
.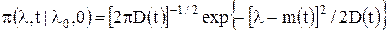 ,
,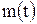 и дисперсия
и дисперсия  даются формулами
даются формулами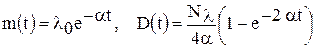 .
.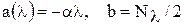 .
.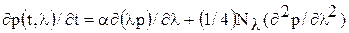 .
.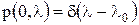 дается приведённой выше условной п.в.
дается приведённой выше условной п.в. 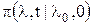 .
.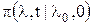 показан на рис. 2.6.
показан на рис. 2.6.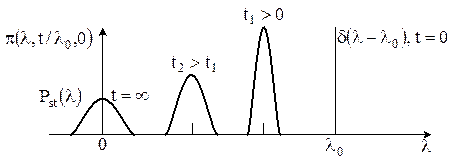
 с течением времени систематически смещается влево из-за ненулевого коэффициента сноса и расплывается все шире и шире из-за коэффициента диффузии, приближаясь к стационарной п.в.
с течением времени систематически смещается влево из-за ненулевого коэффициента сноса и расплывается все шире и шире из-за коэффициента диффузии, приближаясь к стационарной п.в.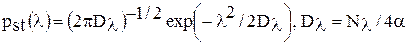 .
.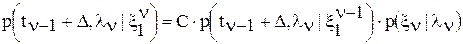 ,
,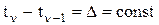 .
. .
.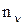 есть гауссовская случайная величина с нулевым м.о. и дисперсией
есть гауссовская случайная величина с нулевым м.о. и дисперсией 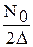 , то на основании уравнения наблюдения, записанного в дискретном варианте, ПВ
, то на основании уравнения наблюдения, записанного в дискретном варианте, ПВ 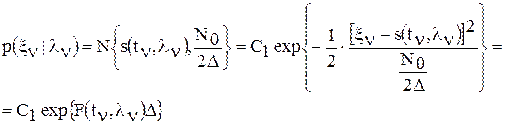
 , т.к.
, т.к. 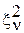 не зависит от
не зависит от 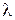 и может быть включён в нормировочную константу
и может быть включён в нормировочную константу 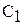 .
.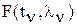 уравнение фильтрации в непрерывном времени после предельного перехода записывается в виде
уравнение фильтрации в непрерывном времени после предельного перехода записывается в виде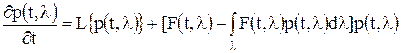 ,
, 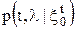 обозначена через
обозначена через 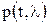 ,
, ,
, ,
,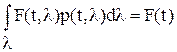 - апостериорное м.о. функции
- апостериорное м.о. функции 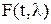 .
.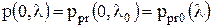 .
. 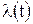 в качестве первого слагаемого, второе слагаемое учитывает результаты наблюдения. В отсутствие наблюдений или при очень большом уровне шума наблюдения
в качестве первого слагаемого, второе слагаемое учитывает результаты наблюдения. В отсутствие наблюдений или при очень большом уровне шума наблюдения  и уравнение Стратоновича переходит в уравнение ФПК.
и уравнение Стратоновича переходит в уравнение ФПК.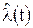 - оптимальная по критерию максимума АПВ оценка сообщения
- оптимальная по критерию максимума АПВ оценка сообщения 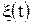 . Располагая АПВ
. Располагая АПВ 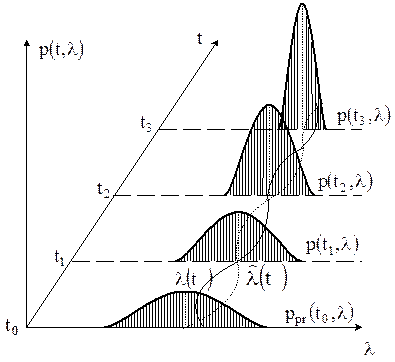
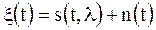 ,
, 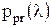 . Так как значение параметра λ за время наблюдения не изменяется:
. Так как значение параметра λ за время наблюдения не изменяется: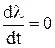 ,
,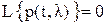 , и уравнение Стратоновича для АПВ параметра λ имеет вид
, и уравнение Стратоновича для АПВ параметра λ имеет вид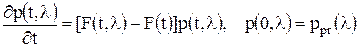 .
. 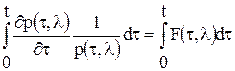 ,
,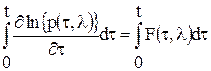 .
.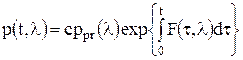 .
. 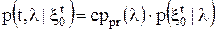 ,
, 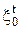
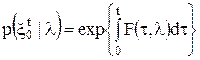 .
.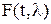 - это производная по времени от логарифма функционала правдоподобия.
- это производная по времени от логарифма функционала правдоподобия. .
. 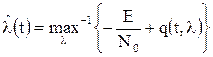 ,
, 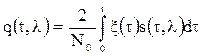 - корреляционный интеграл,
- корреляционный интеграл, 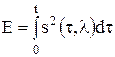 - энергия сигнала.
- энергия сигнала.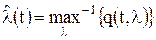
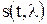 и шума
и шума 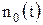 , неизвестен сам факт наличия сигнала
, неизвестен сам факт наличия сигнала 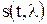 . С целью формализации задачи запишем колебание
. С целью формализации задачи запишем колебание 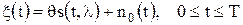 .
. 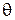 – дискретная сл.в., принимающая лишь два возможных значения:
– дискретная сл.в., принимающая лишь два возможных значения: 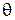 =0 (сигнал отсутствует) и
=0 (сигнал отсутствует) и 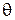 =1 (сигнал присутствует). Требуется по принятой конкретной реализации
=1 (сигнал присутствует). Требуется по принятой конкретной реализации 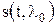 значение параметра l априорно точно известно и равно l0, т.е.
значение параметра l априорно точно известно и равно l0, т.е.  . Этот случай важен потому, что определяет предельные (потенциальные) возможности (верхние границы) для характеристик обнаружения.
. Этот случай важен потому, что определяет предельные (потенциальные) возможности (верхние границы) для характеристик обнаружения.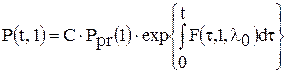 .
.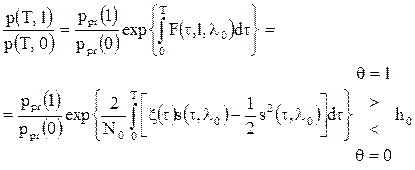
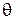 неизвестны (что фактически соответствует
неизвестны (что фактически соответствует 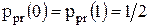 ), то отношение апостериорных вероятностей переходит в отношение правдоподобия.
), то отношение апостериорных вероятностей переходит в отношение правдоподобия.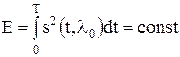 .
.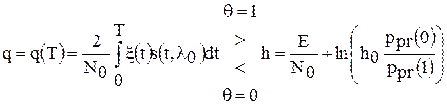 .
. 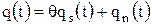 , где
, где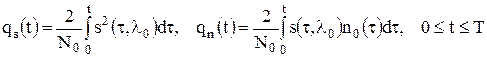 .
. 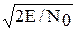 . Соответствующее отношение по мощности
. Соответствующее отношение по мощности 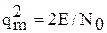 .
.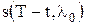 .
.



