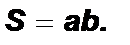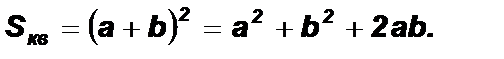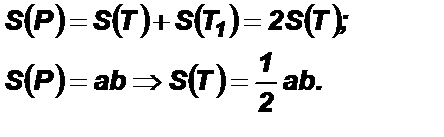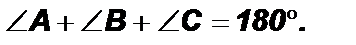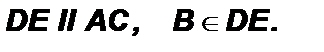Площадь прямоугольника, прямоугольного треугольника и площадь квадрата.

Определение 1. Для многоугольных фигур площадью называется положительная величина с такими свойствами: 1) Если фигура составлена из нескольких многоугольных фигур, то ее площадь равна сумме площадей этих фигур. 2) Равные треугольники имеют  равную площадь.

Определение 2. Фигуры, имеющие одну и ту же площадь, называются равновеликими.

b

b

a

a

Измерение площади состоит в сравнении площади данной фигуры с площадью фигуры, принятой за единицу измерения. В результате сравнения получается некоторое число, принятое за численное значение площади. Это число показывает, во сколько раз площадь данной фигуры больше (или меньше) площади фигуры, принятой за единицу измерения  площади. За единицу измерения площади принимает площадь подходящего квадрата. Площадь этого квадрата называют квадратной единицей площади, а сам квадрат – единичным.

Теорема о площади прямоугольника. Площадь прямоугольника равна произведению его сторон:

Доказательство:

Рассмотрим прямоугольник со сторонами a и b и площадью S.

2) Достроим прямоугольник до квадрата со стороной a + b, как показано на рисунке. Площадь квадрата равна квадрату его стороны, поэтому

3) Из рисунка видно, что квадрат составлен из двух прямоугольников со сторонами a и b и двух квадратов, причем один из них со стороной a имеет площадь a ², а второй – со стороной b имеет площадь b ².

Следовательно, площадь каждого прямоугольника равна

Теорема о площади прямоугольного треугольника. Площадь прямоугольного треугольника равна половине произведения его катетов.

Доказательство: Пусть дан прямоугольный треугольник Т со сторонами a и b. Достроим его до прямоугольника Р со сторонами a и b, проведя через вершины его острых углов прямые, перпендикулярные катетам. Гипотенуза треугольника разбивает прямоугольник на два равных треугольника Т и Т₁. Поэтому

Площадь квадрата

Задача по теме «Элементы треугольника»

Билет № 8

1. Определение треугольника. Доказать теорему о сумме углов треугольника. Замечательные точки треугольника: центр тяжести, ортоцентр, центры вписанной, описанной и вневписанной окружностей.

Треуго́льник — многоугольник, имеющий 3 вершины и 3 стороны; часть плоскости, ограниченная тремя точками, не лежащими на одной прямой, и тремя отрезками, попарно соединяющими эти точки.

Теорема о сумме углов треугольника: Сумма внутренних углов треугольника равна 180°.

E

D

C

B

A

Дано:     ∆АВС.

Доказать:

Доказательство:

1. Проведем

 

Следствие 1. У любого треугольника хотя бы два угла острые.

Допустим, что у треугольника один острый угол или вообще нет острых углов. Тогда у этого треугольника есть хотя бы два угла, каждый из которых не меньше 90°, а сумма этих углов не меньше 180°. Это невозможно, так как сумма углов треугольника равна 180°. 

Следствие 2. Если два угла одного треугольника соответственно равны двум углам другого треугольника, то и третьи углы этих треугольников равны.

Допустим, что у треугольников АВС и МРТ соответственно равны углы: ÐА = ÐМ, ÐВ = ÐР. Тогда ÐС = 180° - (ÐА + ÐВ), ÐТ = 180° - (ÐМ + ÐР). Следовательно, ÐС = ÐТ.

Следствие 3.   У прямоугольного треугольника сумма острых углов равна 90 °.

Так как у прямоугольного треугольника один из углов прямой, то сумма двух других его углов равна 180° - 90° = 90°.

Следствие 4. У равнобедренного прямоугольного треугольника острые углы имеют градусную меру 45 °.

Так как у прямоугольного треугольника один из углов прямой, то сумма двух других его углов равна 180° - 90° = 90°. Поскольку эти углы равны, то градусная мера каждого 90°: 2 = 45°.

Следствие 5. У равностороннего треугольника все углы имеют градусную меру 60 °.

Так как у равностороннего треугольника все углы равны между собой, а их сумма равна 180°, то градусная мера каждого угла равна 180°: 3 = 60°.

P

М

К

С

В

А

Биссектрисой треугольника называется отрезок, делящий внутренний угол треугольника пополам и проведенный из вершины до пересечения с противоположной стороной. АК – биссектриса угла А.

Медианой треугольника называ­ется отрезок, соединяющий вершину треугольника с середи­ной противоположной стороны. CM – медиана, проведенная к сто­роне АВ (АМ = МВ).

Высотой треугольника называ­ется отрезок перпендикуляра, опущенный из вершины треугольника на противоположную сторону. ВР – высота, опущенная на сто­рону АС.

P

N

K

C

B

N

K

B

C

C1

B1 P

A1

A

O

A

C

B

A

N

K

P

O

Точка пересечения биссектрис треугольника называется инцентром и является центром вписанной окружности.