
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Линейная среднеквадратическая регрессия
Построим линейную регрессионную модель в виде:
Коэффициенты теоретической регрессии
Представим зависимость этих измерений в линейном виде, аналогичном регрессионной модели.
здесь
Используя то, что наши данные измерений приведены к стандартному масштабу, где
можно заметить, что если Учитывая это, запишем уравнения эмпирической регрессии в индексном и в матричном виде:
Запишем также условие минимальности дисперсии невязок в виде:
который показывает, что условие минимальности дисперсии невязок эквивалентно главному принципу метода наименьших квадратов (МНК).
Учитывая, что минимум положительно определённой квадратичной формы достигается в стационарной точке, получим:
Найденные коэффициенты регрессии
Построенная регрессия с коэффициентами
Коэффициент детерминации показывает долю объяснённой дисперсии в общей наблюдаемой дисперсии (изменчивости) объясняемой величины. К свойствам коэффициента необходимо отнести следующее:
Последнее соотношение позволяет определить значимость коэффициента детерминации по критерию Фишера.
Коэффициент значим по уровню
Числовой пример (часть 3) В части 1 нашего сквозного примера для наблюдаемых исходных измерений была построена матрица измерений в стандартной форме (центрированная и нормированная). Построим по ней линейную регрессию (тренд), для этого вычислим коэффициенты регрессии
0.053 |
| R2= |
0.919 | значим | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Х"У= | 9.054 | в= |
0.538 |
| Fнабл= | 16.9069 |
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| -8.516 |
| -0.210 |
| Fкрит= | 4.53369 |
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| 8.113 |
|
0.446 |
| G= |
4.53369 |
|
5.2. Теорема Гаусса-Маркова
Коэффициент детерминации является важным обобщающим критерием качества регрессии, но он не единственный и не отвечает на ряд важных вопросов о соответствии построенной методом наименьших квадратов эмпирической регрессии той теоретической линейной регрессионной связи между случайными величинами 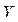 и
и 
|
|
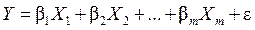 ,
, 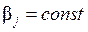 .
.
На поставленный вопрос отвечает теорема Гаусса-Маркова, утверждающая, что если специфические остатки 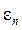 во всех измерениях при наблюдении обладают следующими свойствами (предпосылками МНК [2]):
во всех измерениях при наблюдении обладают следующими свойствами (предпосылками МНК [2]):
1.  , несмещ`нность остатков,
, несмещ`нность остатков,
2.  , гомоскедастичность остатков,
, гомоскедастичность остатков,
3.  при
при 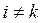 , некоррелируемость остатков между собой. Условия 2-3 могут быть записаны в виде
, некоррелируемость остатков между собой. Условия 2-3 могут быть записаны в виде  ,
,  .
.
4.  , некоррелируемость остатков и объясняющих переменных.
, некоррелируемость остатков и объясняющих переменных.
5. 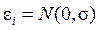 , нормальность остатков.
, нормальность остатков.
Тогда построенная по методу МНК эмпирическая регрессия
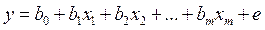
является несмещённой, состоятельной и эффективной оценкой для теоретической регрессии.
Это означает, что оценки  обладают следующими свойствами:
обладают следующими свойствами:
1. 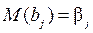 , несмещённость
, несмещённость
2.  , состоятельность
, состоятельность
3.  , эффективность.
, эффективность.
Рассмотрим некоторые следствия теоремы Гаусса-Маркова. Величина  является неизвестной и неизмеримой в наблюдениях, ее эмпирическим аналогом является величина
является неизвестной и неизмеримой в наблюдениях, ее эмпирическим аналогом является величина 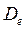 , однако
, однако  , но эту смещённость можно исправить, введя величину
, но эту смещённость можно исправить, введя величину
 ,
,
для которой  , то есть смещение отсутствует. Величина
, то есть смещение отсутствует. Величина 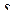 называется стандартной ошибкой регрессии. Через нее выражаются следующие важные величины:
называется стандартной ошибкой регрессии. Через нее выражаются следующие важные величины:
 ,
,
называемые стандартными ошибками коэффициентов регрессии. Кроме того, доказано [1], что отклонение  пропорционально величине Стьюдента
пропорционально величине Стьюдента
 .
.
Последнее равенство позволяет построить, во-первых, доверительные интервалы для коэффициентов теоретической регрессии с надежностью 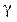
 , где
, где 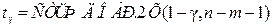 ,
,
а во-вторых, проверить значимость по уровню 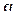 коэффициентов эмпирической регрессии
коэффициентов эмпирической регрессии 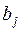 по критерию Стьюдента:
по критерию Стьюдента:
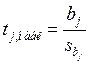 ,
,  ,
, 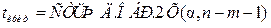 .
.
Коэффициент регрессии 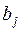 является значимым (значимо отличным от нуля), если его жёсткость
является значимым (значимо отличным от нуля), если его жёсткость 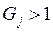 . Значимость коэффициента регрессии говорит о значимости переменной в модели регрессии, что позволяет решать проблему спецификации модели регрессии со стороны отбрасывания незначимых для модели переменных. Однако, отбрасывая незначимую переменную, мы не должны значимо уменьшать коэффициент детерминации. Если это происходит, то незначимая переменная видимо коррелирует с другими уже значимыми переменными. В этом случае отбрасывание переменных нежелательно.
. Значимость коэффициента регрессии говорит о значимости переменной в модели регрессии, что позволяет решать проблему спецификации модели регрессии со стороны отбрасывания незначимых для модели переменных. Однако, отбрасывая незначимую переменную, мы не должны значимо уменьшать коэффициент детерминации. Если это происходит, то незначимая переменная видимо коррелирует с другими уже значимыми переменными. В этом случае отбрасывание переменных нежелательно.
Числовой пример (часть 4 )
Продолжая сквозной пример, вычислим стандартные ошибки регрессии, доверительные интервалы для коэффициентов теоретической регрессии 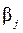 и значимость эмпирических коэффициентов
и значимость эмпирических коэффициентов 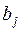 .
.
Стандартная ошибка регрессии  , а ошибки коэффициентов и их доверительные интервалы при заданной надёжности
, а ошибки коэффициентов и их доверительные интервалы при заданной надёжности  будут:
будут:
|
|
0.053 |
| 0.126 |
| -0.193 |
| 0.299 |
| в= |
0.538 | Sb= | 0.159 |
| 0.229 |
| 0.846 |
|
| -0.210 |
| 0.172 |
| -0.545 | 0.126 | |
|
|
0.446 |
| 0.135 |
| 0.184 |
| 0.708 |
Расчёт значимости коэффициентов показывает следующее:
|
| 0.170874 |
| 0 | R2= |
0.663 | незачим |
| G= | 1.382713 | bзнач= | 0.538 | Fнабл= | 2.947689 |
|
|
| -0.49669 |
| 0 | Fкрит= | 4.533689 |
|
|
| 1.352548 |
| 0.446 | G= |
0.650175 |
|
Видим, что коэффициенты  и
и  незначимы при заданном уровне значимости
незначимы при заданном уровне значимости 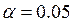 . Отбрасывая незначимые переменные получим регрессию только по двум переменным
. Отбрасывая незначимые переменные получим регрессию только по двум переменным 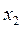 и
и 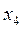 , однако коэффициент детерминации при этом резко уменьшается и становится не значимым. Переменные
, однако коэффициент детерминации при этом резко уменьшается и становится не значимым. Переменные 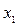 и
и 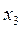 вместе отбрасывать нельзя, так как они влияют на значимые переменные. Отбросим только переменную
вместе отбрасывать нельзя, так как они влияют на значимые переменные. Отбросим только переменную 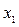 , тогда получим следующее:
, тогда получим следующее:
|
|
|
| 0 | R2= |
0.951 | зачим |
| bзнач= | 0.538 | Fнабл= | 29.42684 |
|
|
| -0.210 | Fкрит= | 4.533689 |
|
|
| 0.446 | G= |
6.490705 |
|
Получается что, регрессионная модель вида  без учёта
без учёта 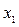 (урожайность земельного участка) имеет более высокий коэффициент детерминации, чем с её учётом. Так решаются некоторые вопросы спецификации модели.
(урожайность земельного участка) имеет более высокий коэффициент детерминации, чем с её учётом. Так решаются некоторые вопросы спецификации модели.
5.3. Проверка предпосылок МНК по входным данным
Для того, чтобы построенная методом МНК линейная регрессия обладала нужными качествами, необходимо выполнение условий (предпосылок) Гаусса-Маркова на наблюдаемые переменные  . Но об их свойствах мы можем судить только по их наблюдениям, поэтому в наблюдательных данных не должны проявляться нарушения предпосылок Гаусса-Маркова. К нарушениям этих предпосылок относятся:
. Но об их свойствах мы можем судить только по их наблюдениям, поэтому в наблюдательных данных не должны проявляться нарушения предпосылок Гаусса-Маркова. К нарушениям этих предпосылок относятся:
- гетероскедастичность данных  ,
,
- автокорреляция данных  в частности
в частности 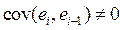
- мультиколлинеарность данных  .
.
Рассмотрим проявление этих нарушений, их значимость и методы устранения.
Гетероскедастичность (неодинаковость) остатков регрессии, их зависимость от переменных 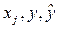 . Это явление можно обнаружить, построив графические зависимости для
. Это явление можно обнаружить, построив графические зависимости для 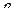 от указанных величин, или вычислив коэффициенты корреляции
от указанных величин, или вычислив коэффициенты корреляции  , значимость которых говорит о наличии гетероскедастичности в данных.
, значимость которых говорит о наличии гетероскедастичности в данных.
 Рис. 5.1. Гетероскедастичность данных. Слева случай отсутствия гетероскедастичности
Рис. 5.1. Гетероскедастичность данных. Слева случай отсутствия гетероскедастичности
Согласно тесту Глейзера [9,10], построив парную регрессионную зависимость  , можно проверить её значимость по критерию Стьюдента, но при этом гетероскедастичность может присутствовать в данных и в случае незначимого коэффициента детерминации. Наиболее популярным и строгим является тест ранговой корреляции Спирмена, согласно которому вычисляется коэффициент ранговой корреляции:
, можно проверить её значимость по критерию Стьюдента, но при этом гетероскедастичность может присутствовать в данных и в случае незначимого коэффициента детерминации. Наиболее популярным и строгим является тест ранговой корреляции Спирмена, согласно которому вычисляется коэффициент ранговой корреляции:
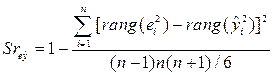 ,
,
где 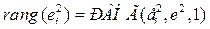 есть порядковый номер элемента
есть порядковый номер элемента 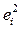 в массиве квадратов остатков
в массиве квадратов остатков 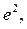 расположенном по возрастанию. Если ранги остатков и объяснённой части
расположенном по возрастанию. Если ранги остатков и объяснённой части 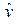 точно соответствуют друг другу (
точно соответствуют друг другу (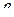 зависит от
зависит от 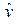 ), то
), то  , если же ранги распределены случайно друг относительно друга, то
, если же ранги распределены случайно друг относительно друга, то 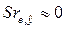 . Доказано [1], что:
. Доказано [1], что:

и, следовательно, для определения значимости 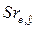 можно воспользоваться критерием Стьюдента при заданном уровне значимости
можно воспользоваться критерием Стьюдента при заданном уровне значимости  . Если коэффициент ранговой корреляции оказывается значимым, то в наблюдательных данных присутствует гетероскедастичность, что может привести к смещению построенной эмпирической регрессии по отношению к истинной теоретической регрессии между наблюдаемыми переменными. В случае гетероскедастичности необходимо отказаться от измеренных данных и повторить их заново, или провести их преобразование (видоизменение, отсев).
. Если коэффициент ранговой корреляции оказывается значимым, то в наблюдательных данных присутствует гетероскедастичность, что может привести к смещению построенной эмпирической регрессии по отношению к истинной теоретической регрессии между наблюдаемыми переменными. В случае гетероскедастичности необходимо отказаться от измеренных данных и повторить их заново, или провести их преобразование (видоизменение, отсев).
|
|
Автокорреляция (самозависимость) остатков регрессии является простейшим частным случаем зависимости остатков между собой. При автокорреляции 1-го порядка соседние остатки регрессии жёстко связаны между собой.
 Рис. 5.2. Автокорреляция в данных,
Рис. 5.2. Автокорреляция в данных,  , положительная автокорреляция
, положительная автокорреляция 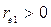 , отрицательная автокорреляция
, отрицательная автокорреляция  .
.
Моделью автокорреляции 1-го порядка является регрессионная зависимость остатков со сдвигом на один элемент 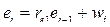 . Если обычный коэффициент корреляции
. Если обычный коэффициент корреляции 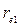 , значим, то это говорит о наличии автокорреляции, однако при его незначимости автокорреляция в данных всеже может быть. Для более строгого определения автокорреляции обычно используется критерий Дарбина-Уотсона
, значим, то это говорит о наличии автокорреляции, однако при его незначимости автокорреляция в данных всеже может быть. Для более строгого определения автокорреляции обычно используется критерий Дарбина-Уотсона  [9,10]:
[9,10]:
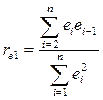 ,
,  .
.
Распределение критерия  отличается крутизной наклона от Стьюдентовского (рис. 2.8) и приводится на рис.5.3, где показаны критические области при проверке гипотезы
отличается крутизной наклона от Стьюдентовского (рис. 2.8) и приводится на рис.5.3, где показаны критические области при проверке гипотезы  :
:

Рис. 5.3. Критерий Дарбина=Уотсона
Значение критерия Дарбина-Уотсона  , что соответствует значениям коэффициента корреляции
, что соответствует значениям коэффициента корреляции  . Критические точки распределения определяются по таблицам в приложение №2 (в Exel нет обратной функции этого распределения). В силу особенностей распределения критерия они как бы расщепляются на две пары точек
. Критические точки распределения определяются по таблицам в приложение №2 (в Exel нет обратной функции этого распределения). В силу особенностей распределения критерия они как бы расщепляются на две пары точек 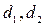 , и
, и 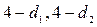 между которыми критерий не даёт ответа на вопрос о значимости коэффициента автокорреляции, в остальном всё аналогично критерию Стьюдента.
между которыми критерий не даёт ответа на вопрос о значимости коэффициента автокорреляции, в остальном всё аналогично критерию Стьюдента.
Мультиколинеарность («параллельность») измеряемых величин говорит о наличии среди измеряемых величин жёстко коррелирующих пар величин. Такая зависимость измеряемых в наблюдениях величин приводит к большим ошибкам коэффициентов регрессии или даже невозможности построить саму регрессию в силу необратимости матрицы парных корреляций. Именно по этой матрице может быть определена жёсткая связь переменных. Одну из коррелирующих величин необходимо исключить из спецификации регрессионной модели. Однако, необходимо помнить, что исключаемая переменная может опосредованно влиять или зависеть от других переменных модели. Поэтому, для исключения переменной из модели, нужен анализ не только парных корреляций, но и частных (очищенных) корреляций, или преобразовать эту переменную каким-либо образом. Подобные преобразования рассматриваются ниже.
Числовой пример (часть 5)
Рассмотрим выполнение предпосылок Гаусса-Маркова в нашем сквозном примере статистического анализа.
Наличие автокорреляции можно допустить, анализируя график остатков от номеров измерений, по крайней мере, в первой и второй половине измерений. Однако в целом, вычисленный коэффициент корреляции остатков  мал, а критерий Дарбина-Уотсогна наблюдается в районе значения 2, казалось бы, что автокорреляция 1-го порядка отсутствует. Но критические значения критерия
мал, а критерий Дарбина-Уотсогна наблюдается в районе значения 2, казалось бы, что автокорреляция 1-го порядка отсутствует. Но критические значения критерия  при нашем объёме выборки таковы, что наблюдаемое значение критерия находится между ними. Вывод состоит в том, что критерий не может определить наличие или отсутствие автокорреляции.
при нашем объёме выборки таковы, что наблюдаемое значение критерия находится между ними. Вывод состоит в том, что критерий не может определить наличие или отсутствие автокорреляции.
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
| Тест Дарбина-Уотсона | |||
|
|
|
|
|
|
|
| ||
|
|
|
|
|
| 0.070 | |||
|
|
|
|
|
|
| |||
|
|
|
|
|
| DWнабл= | 1.859 | ||
|
|
|
|
|
| d1крит= |
| 0.440 | |
|
|
|
|
|
| d2крит= |
| 2.283 | |
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
| d1крит< DWнабл<d2крит | |||
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
| Наличие или отсутствие | |||
|
|
|
|
|
| автокорреляции |
| ||
|
|
|
|
|
| тест не определяет. | |||
Требуются более серьезные исследования, но отметим, что при объёме входных данных  в нашем примере ответ о наличии автокорреляции был бы отрицательным.
в нашем примере ответ о наличии автокорреляции был бы отрицательным.
Исследование гетероскедастичности в нашем примере будем проводить, анализируя связь  , так как объяснённая часть
, так как объяснённая часть 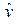 наблюдений является линейной комбинацией наблюдаемых величин. Как графически (шарообразность изображения остатков) на плоскости, так и аналитически по тестам Глейзера и Спирмена видим, что значимое наличие гетероскедастичности данных не устанавливается.
наблюдений является линейной комбинацией наблюдаемых величин. Как графически (шарообразность изображения остатков) на плоскости, так и аналитически по тестам Глейзера и Спирмена видим, что значимое наличие гетероскедастичности данных не устанавливается.
|
|
|
|
|
|
|
|
| |||
|
|
|
|
|
|
|
|
| |||
| -0.690 | 0.016 |
|
|
|
|
|
| |||
| 0.330 | -0.204 |
|
|
|
|
|
| |||
| -1.299 | 0.526 |
|
|
|
|
|
| |||
| 0.701 | -0.075 |
|
|
|
|
|
| |||
| 1.250 | 0.375 |
|
|
|
|
|
| |||
| -0.949 | 0.126 |
|
|
|
|
|
| |||
| 0.410 | -0.384 |
|
|
|
|
|
| |||
| -0.337 | -0.366 |
|
|
|
|
|
| |||
| -0.501 | -0.293 |
|
|
|
|
|
| |||
| -0.828 | 0.064 |
|
|
|
|
|
| |||
| 1.913 | 0.212 |
|
|
|
|
|
| |||
|
|
|
|
|
|
|
|
| |||
|
|
|
|
|
|
|
|
| |||
| РАНГ | РАНГ |
|
|
|
|
|
| |||
|
|
|
|
|
|
|
|
| |||
| 5 | 1 |
|
|
|
|
|
| |||
| 1 | 5 |
|
| Тест Глейзера |
|
| ||||
| 10 | 11 |
|
|
| tнабл= | 0 |
| |||
| 6 | 3 |
|
| 0.000 | tкрит= | 2.262 |
| |||
| 9 | 9 |
|
|
| незначим |
| ||||
| 8 | 4 |
|
|
|
|
|
| |||
| 3 | 10 |
|
| Тест Спирмена |
|
| ||||
| 2 | 8 |
|
|
| tнабл= | 0.246 |
| |||
| 4 | 7 |
|
| 0.082 | tкрит= | 2.262 |
| |||
| 7 | 2 |
|
|
| незначим |
| ||||
| 11 | 6 |
| Гетероскедастичности |
|
|
| ||||
|
|
|
| в данных нет |
|
|
| ||||
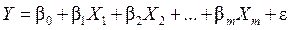 .
. необходимо определить из выше приведённых условий А и Б, на основе наблюдательных статистических данных, собранных в матрицу измерений
необходимо определить из выше приведённых условий А и Б, на основе наблюдательных статистических данных, собранных в матрицу измерений  и измеренный вектор
и измеренный вектор  объёма
объёма  .
.

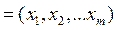 ;
; 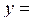
 ,
, 

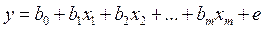 ,
,  ,
, - объяснённая часть измерений, а
- объяснённая часть измерений, а  - невязка измерений и линейной модели. Подберём неизвестные коэффициенты эмпирической регрессии
- невязка измерений и линейной модели. Подберём неизвестные коэффициенты эмпирической регрессии  из условий
из условий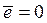 ,
, 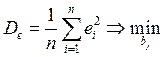 .
. ,
,  можно увидеть, что коэффициент
можно увидеть, что коэффициент  . Действительно, вычисляя средние значения и величины дисперсии
. Действительно, вычисляя средние значения и величины дисперсии ,
, 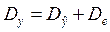
 и
и  .
.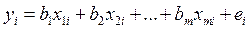 ,
,  :
: ,
,  ,
,  .
.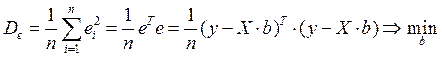 ,
,



 доставляют минимум дисперсии невязки регрессии. Сама невязке вычисляется так:
доставляют минимум дисперсии невязки регрессии. Сама невязке вычисляется так: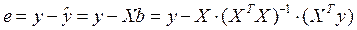 .
. , называемая также линейным трендом, объясняет величину
, называемая также линейным трендом, объясняет величину  через величины
через величины  не полностью, а лишь частично в силу
не полностью, а лишь частично в силу  . В качестве меры объяснения удобно принять величину дисперсии
. В качестве меры объяснения удобно принять величину дисперсии 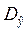 или, как её называют, величину изменчивости переменной. При этом безразмерный коэффициент
или, как её называют, величину изменчивости переменной. При этом безразмерный коэффициент  называется коэффициентом детерминации:
называется коэффициентом детерминации: .
. ,
, 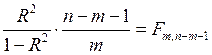 .
.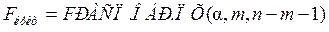 ,
, 
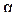 , если жёсткость критерия
, если жёсткость критерия  больше единицы, при этом и сама регрессия называется значимой. Незначимая регрессия не обладает достаточным качеством и не имеет практического применения. Чем выше жёсткость критерия, тем качественнее является регрессия с точки зрения объяснения объясняемой величины.
больше единицы, при этом и сама регрессия называется значимой. Незначимая регрессия не обладает достаточным качеством и не имеет практического применения. Чем выше жёсткость критерия, тем качественнее является регрессия с точки зрения объяснения объясняемой величины.











