
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Основные задачи и методы математической статистики
Для установления закономерностей, которым подчинены случайные события и случайные величины, теория вероятности, как и любая другая наука, обращается к опыту – наблюдениям, измерениям, экспериментам. Результаты наблюдений за случайными величинами объединяются в наборы статистических данных. Задачей математической статистики, раздела современной теории вероятностей, является разработка методов сбора и обработки статистических данных, а также их анализа с целью установления законов распределения наблюдаемых случайных величин [2]. Выборочный метод Генеральной совокупностью является набор всех мыслимых статистических данных, при наблюдениях случайной величины:
Наблюдаемая случайная величина Х называется признаком или фактором выборки. Генеральная совокупность есть статистический аналог случайной величины, её объем N обычно велик, поэтому из неё выбирается часть данных, называемая выборочной совокупностью или просто выборкой
Использование выборки для построения закономерностей, которым подчинена наблюдаемая случайная величина, позволяет избежать её сплошного (массового) наблюдения, что часто бывает ресурсоёмким процессом, а то и просто невозможным. Однако выборка должна удовлетворять следующим основным требованиям: - выборка должна быть представительной, т.е. сохранять в себе пропорции генеральной совокупности, - объём выборки должен быть небольшим, но достаточным для того, чтобы полученные результаты её анализа обладали необходимой степенью надёжности, - данные в выборке не должны бать «засорены» грубыми измерениями, содержащими нетипично большие ошибки измерений. Отметим, что в более строгом смысле выборку можно представить как случайную многомерную величину Возможные значения элементов выборки
Упорядоченный по возрастанию значений набор вариант совместно с соответствующими им частотами называется вариационно-частотным рядом выборки:
Ломаная линия, соединяющая точки вариационно-частотного ряда на плоскости Вариационно-частотный ряд имеет существенный недостаток, а именно, ненаглядность полигона в случае малой повторяемости вариант, например, при наблюдении непрерывного признака его повторяемость в выборке маловероятна. Более общей формой описания элементов выборки является гистограмма выборки. Для построения гистограммы разобьём интервал значений выборки
Совокупность интервалов, наблюдаемой в выборке случайной величины и соответствующих им частот, называется гистограммой выборки. Различаются гистограммы частот, относительных частот и плотности частоты и обозначаются соответственно:
Для частот гистограммы выполнены следующие условия нормировки:
Число интервалов гистограммы m должно быть оптимальным, чтобы, с одной стороны, была достаточной повторяемость интервалов, а с другой стороны не должны сглаживаться особенности выборочной статистики. Рекомендуется значение
Помимо полигона и гистограммы выборка характеризуется следующими основными числовыми характеристиками:
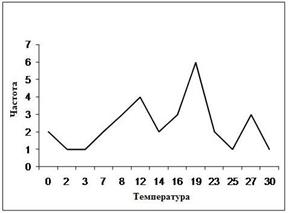
отклонение (выборочный стандарт). Пусть, например, дана выборка полуденных температур месяца Май своим вариационно-частотным рядом с объёмом
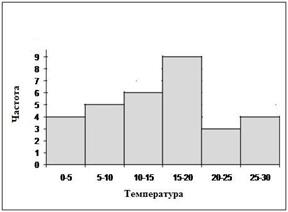
Полигон и гистограмма данной выборки приводятся ниже на рис.2.1.
Рис. 2.1. Полигон и гистограмма частот выборки
Расчёт основных выборочных характеристик может быть легко проведен с помощью статистических функций приложения Excel-13:
Отметим, что все числовые характеристики выборки являются случайными величинами, поскольку получены по случайно взятой выборке. На элементах другой выборки наблюдений над той же случайной величиной
Рассмотрим выборочные распределения нормальных выборок. Если наблюдаемая случайная величина
и построим из них случайные величины Пирсона
Отсюда видно, что случайная величина выборочной дисперсии DВ распределена пропорционально «Хи-квадрат» случайной величине с n-1 степенью свободы, а отклонение выборочного среднего от математического ожидания распределено пропорционально t -величине Стьюдента с n-1 степенью свободы. При сравнении двух выборок объёмов n 1 и n2 часто используется случайная величина Фишера [8] со степенями свободы n1 и n2:
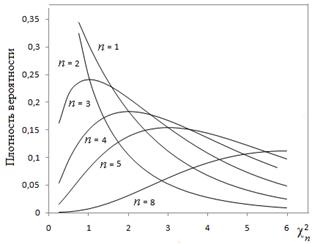
Распределения этих величин, как функций от стандартных нормальных величин, хорошо изучены и построены их функции распределения, обратного распределения и плотности вероятности распределения. Ниже рис. 2.2.-2.4 представлены графики и функции Excel для их вычисления.
Рис. 2.2. Функции распределения величины Пирсона
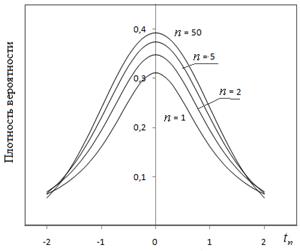
Рис. 2.3. Функции распределения величины Стьюдента
Рис. 2.4. Функции распределения величины Фишера
Статистические оценки Пусть распределение наблюдаемой случайной непрерывной величины Точечной статистической оценкой параметров распределения или характеристик наблюдаемой случайной величины
Например, статистическими оценками математического ожидания величины могут быть такие оценки: Оценка Оценка должна быть несмещенной, т.е. её математическое ожидание должно совпадать с истинным значением параметра для любого объёма n
или хотя бы асимптотически несмещённой: Оценка должна быть состоятельной, т.е. с ростом объёма выборки оценка должна сходиться по вероятности к истинному значению параметра:
Для состоятельности оценки достаточно выполнения следующего:
Построенная оценка для использования на практике должна быть эффективной, т.е. её дисперсия должна быть минимальной среди всех возможных оценок при фиксированном объёме выборки:
Коэффициент эффективности оценки Отметим, что на практике не всегда удаётся удовлетворить всем перечисленным требованиям к оценке, но введённые свойства оценок позволяют проранжировать имеющиеся оценки по их качеству. Как пример рассмотрим оценки математического ожидания Построим точечные оценки:
и рассмотрим их свойства. Поскольку можно вычислить, что для оценки m* справедливо:
то из этого следует несмещённость и состоятельность оценки m*. Рассматривая же оценку
Из чего следует состоятельность, но смещённость оценки
Оценка В отличие от точечных оценок типа Надёжностью оценки (доверительной вероятностью) называется вероятность
Полуширина доверительного интервала Пусть в выборке Построим доверительный интервал для математического ожидания m:
принимая за точечную оценку m, величину Решение уравнения
Его решение получим в виде
Рис. 2.5. Двухсторонняя квантиль Стьюдента
Построим теперь доверительный интервал для среднеквадратического отклонения
Принимая за оценку
тогда получим его решение в виде
Рис. 2.6. Двухсторонняя «хи-квадрат» квантиль
Пример. Наблюдается выборка полуденных температур в Мае объёмом n =31 со средним выборочным значением Исправленное выборочное среднеквадратическое отклонение Через обратное распределение Стьюдента находим 14.87+2.894 < m <14.87+2.894 или 11.976< m <17.674. Для построения доверительного интервала среднеквадратического отклонения через обратное распределение «Хи-квадрат» находим
2.3. Проверка статистических гипотез
Имея дело со случайными величинами, в различных областях человеческой деятельности часто приходится высказывать предположения о виде распределения случайной величины или о значениях её параметров. Эти предположения строятся с целью прогнозирования поведения случайной величины и принятия решений в условиях неопределённости. Статистической гипотезой называется любое предположение о виде распределения случайной величины
Высказанная статистическая гипотеза должна быть проверена по результатам наблюдений (измерений) случайной величины [11], в результате чего, гипотеза принимается или отвергается с определённой степенью риска совершить ошибку. Примером статистической гипотезы может быть предположение о том, что наблюдаемая в выборке случайная величина является нормальной с определёнными значениями параметров:
Выдвинутая статистическая гипотеза Н должна быть проверена. Как и в любой другой науке, критерием её проверки является опыт, т.е. наблюдение (измерение) случайной величины. Критерий проверки должен отвергать или принимать гипотезу по результатам наблюдения. При этом могут быть совершены ошибки двух родов [6]: 1. Отвергнута верная гипотеза с вероятностью 2. Принята не верная гипотеза с вероятностью Исключить эти ошибки полностью невозможно («не ошибается тот, кто ничего не делает»), но их можно постараться минимизировать. Учитывая сказанное, при построении критерия проверки статистической гипотезы необходимо сначала задаться допустимым уровнем риска на совершение ошибки 1 рода, как наиболее значимой, а затем минимизировать ошибки 2 рода.
Пусть необходимо проверить гипотезу Во-первых, в качестве критерия принимается некоторая случайная величина Во-вторых, строится решающее правило для критерия проверки, согласно которому гипотеза будет приниматься или отвергаться. Для этого, назовем критической областью критерия те значения величины
Точки значения критерия Принцип максимального правдоподобия утверждает, что наблюдаемые события имеют большую вероятность и наоборот, маловероятные события ненаблюдаемые. Согласно этому принципу наблюдаемое значение критерия Зададимся вероятностью Если из условия
можно определить критические точки
есть вероятность правильного отбрасывания Таким образом, критическими точками критерия являются квантили его распределения, определенные согласно уровню значимости проверяемой гипотезы.
Рис. 2.7. Двухсторонняя критическая область критерия
На рис. 2.7 приведена графическая интерпретация алгоритма построения критической области одномерного критерия. Видим, что структура критической области зависит от наличия альтернативных гипотез и их «расположения» относительно основной. Рассмотрим примеры. Критерий Смирнова-Граббса. Рассмотрим проблему отсева грубых ошибок при измерении нормальной случайной величины. Пусть мы имеем нормальную выборку наблюдений
Вычисляя значение
Видим, что при значимости проверяемой гипотезы в 10% критерий отклоняет её в пользу гипотезы Критерий Стьюдента о значимости измеренной величины. В статистическом анализе очень часто используются критерии о значимости оценок различных величин, построенных по выборке. Проверяемой гипотезой является гипотеза о том, что истинная теоретическая величина
Рис. 2.8. Критерий Стьюдента проверки значимости величины
Здесь
Значимость проверяемой оценки имеет место быть при жёсткости Например, в качестве проверяемой величины часто используется выборочный коэффициент корреляции между двумя выборками
Критерием является следующая величина Стьюдента:
Измерительные данные, с которыми работает инженер-исследователь или аналитик в процессах проектирования, производства, эксплуатации и мониторинга различных технических, экологических, социально-экономических систем редко бывают одномерными. Обычно при исследовании объекта или множества объектов измеряется несколько параметров объекта. Таким образом формируется многомерный статистический набор данных. При строительстве и эксплуатации зданий и сооружений могут быть измерены и запротоколированы множество различных параметров (рис. 3.1).
Рис. 3.1. Факторы влияния на здание
Измеряемые величины в большинстве случаев являются случайными как по своей природе, так и за счёт ошибок измерения
где
Рис. 3.2.Виды измерений
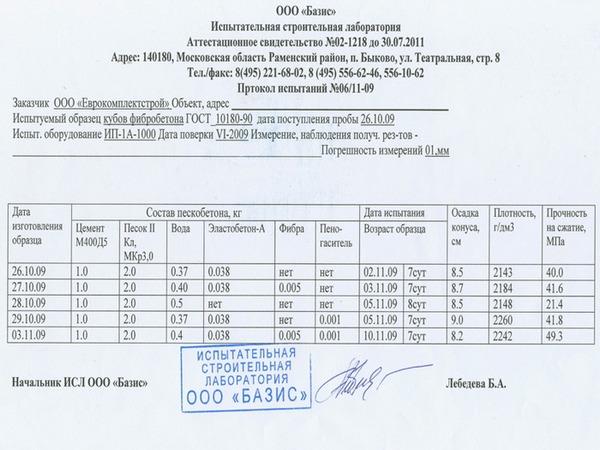
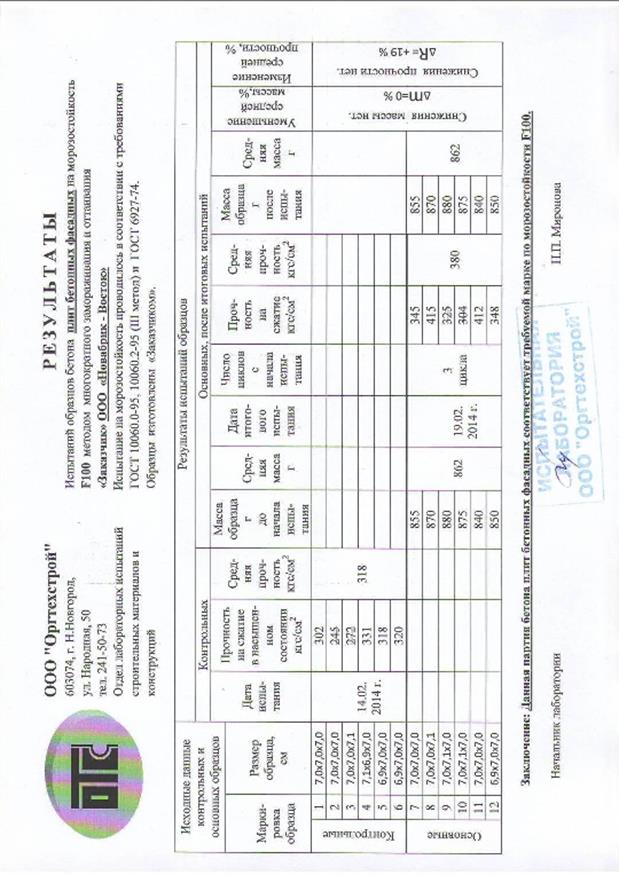
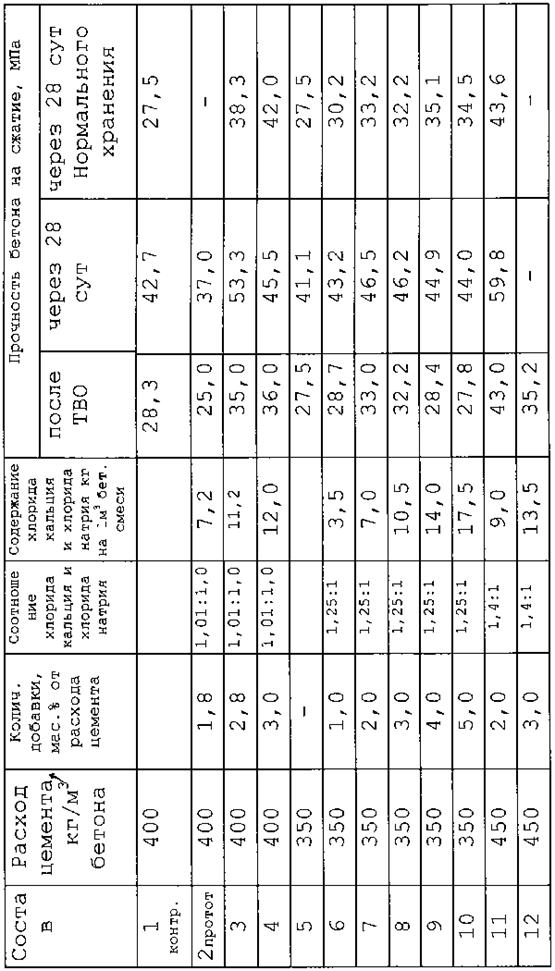
Приведём несколько примеров наборов статистических данных, как документально оформленных измерений.
Многомерность статистических данных состоит в том, что у каждого наблюдаемого объекта
Рис. 3.3. Пространственные и временные ряды данных образуют куб данных
Каждый объект, в своём ряду данных, представляется вектором измерений
Используя все измерения по n объектам, можем вычислить числовые характеристики по каждому измеримому фактору.
Зная средние значения Помимо преобразования в стандартную форму, рекомендуется проверить измерения на грубые ошибки согласно критерию Смирнова-Греббса [9-10]. Рассмотрим пример многомерных статистических данных, которые будем анализировать во всех последующих главах. Пример состоит в анализе данных об n =11 земельных участках, проданных на рынке в течение года. Известны данные о следующих m =4 факторах участка:
| Поделиться:
| |
 .
. ,
, 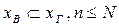 .
.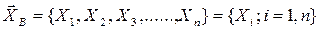 , у которой все компоненты
, у которой все компоненты 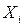 распределены одинаково и по закону распределения наблюдаемой случайной величины. В этом смысле выборочные значения
распределены одинаково и по закону распределения наблюдаемой случайной величины. В этом смысле выборочные значения 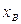 есть одна из реализаций величины
есть одна из реализаций величины 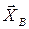 .
.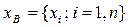 , называются вариантами
, называются вариантами 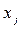 выборки, причём число вариант m меньше, чем объём выборки
выборки, причём число вариант m меньше, чем объём выборки 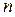 . Варианта может повторяться в выборке несколько раз, число повторения варианты
. Варианта может повторяться в выборке несколько раз, число повторения варианты 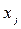 в выборке называется частотой варианты
в выборке называется частотой варианты 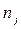 . Причём,
. Причём, 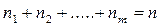 . Величина
. Величина 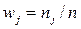 называется относительной частотой варианты
называется относительной частотой варианты 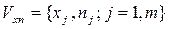 ;
; 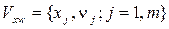 .
.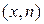 или
или 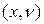 называется полигоном частот.
называется полигоном частот.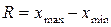 на m интервалов
на m интервалов  длины
длины 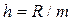 с границами
с границами  . Число элементов выборки
. Число элементов выборки 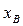 , попадающих в интервал,
, попадающих в интервал,  называется частотой
называется частотой  ~ относительная частота интервала,
~ относительная частота интервала,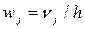 j ~ плотность относительной частоты интервала.
j ~ плотность относительной частоты интервала.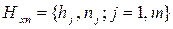 ,
,  ,
, 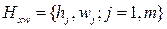 .
. ,
,  ,
, 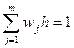
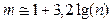 . На плоскости
. На плоскости  ~ выборочное среднее;
~ выборочное среднее;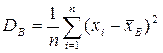 ~ выборочная дисперсия;
~ выборочная дисперсия;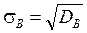 ~ выборочное среднеквадратическое отклонение;
~ выборочное среднеквадратическое отклонение;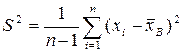 ~ исправленная выборочная дисперсия;
~ исправленная выборочная дисперсия;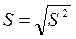 ~ исправленное выборочное среднеквадратическое
~ исправленное выборочное среднеквадратическое  .
.
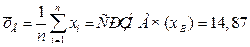 ;
; 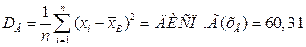 ;
; 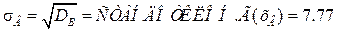 ;
; ;
;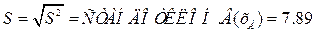 .
.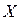 числовые характеристики в общем случае изменят свое значение.
числовые характеристики в общем случае изменят свое значение. , где
, где 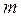 - математическое ожидание,
- математическое ожидание,  - среднеквадратическое отклонение, то случайная величина среднего выборочного
- среднеквадратическое отклонение, то случайная величина среднего выборочного  так же является нормальной
так же является нормальной 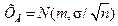 . Здесь
. Здесь  нормальные случайные величины, совпадающие с наблюдаемой величиной. Рассмотрим стандартные нормальные величины
нормальные случайные величины, совпадающие с наблюдаемой величиной. Рассмотрим стандартные нормальные величины 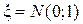 в виде:
в виде: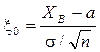 ,
, 
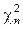 и Стьюдента
и Стьюдента 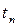 [4,8]:
[4,8]: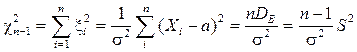 ,
,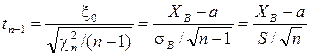 .
.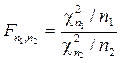 .
.
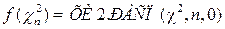 ,
, ,
, ,
,
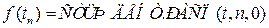 ,
,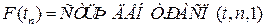 ,
,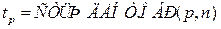 ,
,

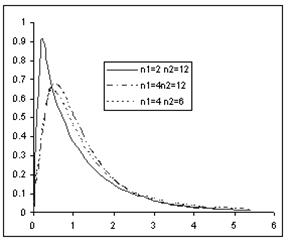
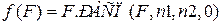 ,
,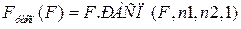 ,
,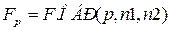 ,
,
 (признак генеральной совокупности) задаётся функцией плотности вероятности
(признак генеральной совокупности) задаётся функцией плотности вероятности 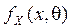 , где
, где 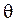 параметр или параметры распределения. Допустим, что вид функции
параметр или параметры распределения. Допустим, что вид функции 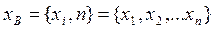 , где n – объём выборки.
, где n – объём выборки.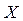 называется построенная по данным выборки объема n величина:
называется построенная по данным выборки объема n величина: .
.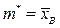 ,
, 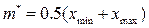 или
или 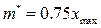 .
. является случайной величиной, т.к. зависит от случайной выборки. Для того, чтобы оценки, получаемые по данным различных выборок соответствовали истинному значению параметра
является случайной величиной, т.к. зависит от случайной выборки. Для того, чтобы оценки, получаемые по данным различных выборок соответствовали истинному значению параметра  , оценка должна удовлетворять следующим требованиям [8].
, оценка должна удовлетворять следующим требованиям [8].
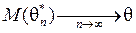 .
. для любого
для любого 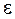
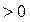 .
.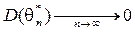 .
.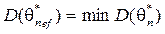 .
.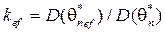 показывает степень эффективности оценки
показывает степень эффективности оценки  , если
, если  , то говорят об асимптотической эффективности оценки.
, то говорят об асимптотической эффективности оценки. и дисперсии
и дисперсии 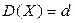 наблюдаемой случайной величины Х.
наблюдаемой случайной величины Х.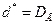
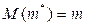 ;
;  при
при 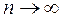 ,
, ,можно получить что:
,можно получить что: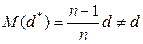 ;
;  .
. Смещёность оценки здесь легко может быть исправлена, если рассмотрим оценку:
Смещёность оценки здесь легко может быть исправлена, если рассмотрим оценку: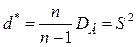 .
. является уже не только состоятельной, но и несмещённой, так как
является уже не только состоятельной, но и несмещённой, так как  . Величина
. Величина  называется исправленной (несмещённой) выборочной дисперсией, а величина
называется исправленной (несмещённой) выборочной дисперсией, а величина 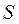 - исправленным среднеквадратическим выборочным отклонением (выборочный стандарт).
- исправленным среднеквадратическим выборочным отклонением (выборочный стандарт). интервальные оценки задают интервал значений, где оцениваемый параметр находится с заданной вероятностью, т.е. это оценки типа
интервальные оценки задают интервал значений, где оцениваемый параметр находится с заданной вероятностью, т.е. это оценки типа  .
.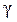 ,с которой оцениваемый параметр находится в интервале:
,с которой оцениваемый параметр находится в интервале: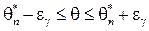 .
.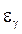 называется точностью оценки, соответствующей надёжности
называется точностью оценки, соответствующей надёжности  . Для построения доверительного интервала (нахождения по
. Для построения доверительного интервала (нахождения по 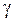 величины
величины  ) необходимо знать закон распределения оценки случайной величины
) необходимо знать закон распределения оценки случайной величины 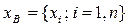 наблюдается нормальная случайная величина
наблюдается нормальная случайная величина  c неизвестными параметрами распределения m и
c неизвестными параметрами распределения m и 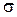 .
. ,
, иучитывая, что величина
иучитывая, что величина 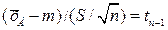 имеет распределение Стьюдента с
имеет распределение Стьюдента с  степенью свободы.
степенью свободы.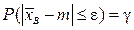 относительно
относительно  при заданном значении
при заданном значении 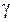 эквивалентно решению уравнения:
эквивалентно решению уравнения: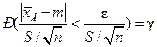 , или
, или  .
. , где
, где  двухсторонняя квантиль Стьюдента (рис. 2.5).
двухсторонняя квантиль Стьюдента (рис. 2.5).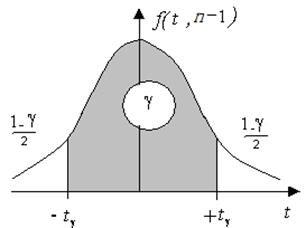
 :
: .
.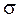 величину
величину 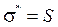 и учитывая, что величина
и учитывая, что величина 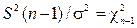 , имеет
, имеет  -распределение с n - 1 степенью свободы. Решение уравнения
-распределение с n - 1 степенью свободы. Решение уравнения 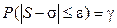 относительно
относительно  эквивалентно решению уравнения:
эквивалентно решению уравнения: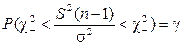 ,
,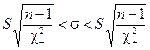 , где величины
, где величины 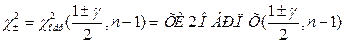 являются правосторонними «хи-квадрат» квантилями (рис. 2.6).
являются правосторонними «хи-квадрат» квантилями (рис. 2.6).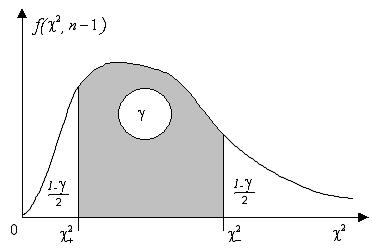
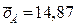 и несмещённой дисперсией
и несмещённой дисперсией 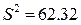 . Построить доверительные интервалы для неизвестного математического ожидания m и среднеквадратического отклонения
. Построить доверительные интервалы для неизвестного математического ожидания m и среднеквадратического отклонения 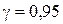 .
.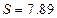 .
.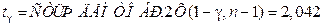 ,тогда
,тогда  и тогда доверительный интервал для математического ожидания m будет:
и тогда доверительный интервал для математического ожидания m будет: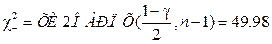
 , тогда:
, тогда: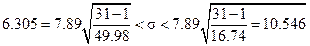 .
. или/и о значении неизвестных параметров распределения
или/и о значении неизвестных параметров распределения  – статистическая гипотеза.
– статистическая гипотеза.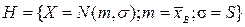 .
.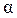 ,
, .
.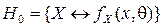 , помимо основной гипотезы
, помимо основной гипотезы  («нулевой») рассмотрим ещё одну или несколько альтернативных гипотез
(«нулевой») рассмотрим ещё одну или несколько альтернативных гипотез 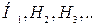 каждая из которых противоречит основной. Построим критерий, однозначно принимающий или отвергающий проверяемую гипотезу по полученной в наблюдении за случайной величиной
каждая из которых противоречит основной. Построим критерий, однозначно принимающий или отвергающий проверяемую гипотезу по полученной в наблюдении за случайной величиной 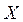 выборке
выборке 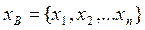 объёма n. Критерий проверки гипотезы состоит из двух составляющих:
объёма n. Критерий проверки гипотезы состоит из двух составляющих: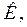 с известным распределением при условии справедливости основной
с известным распределением при условии справедливости основной 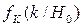 и хотя бы частично известным для альтернативных гипотез
и хотя бы частично известным для альтернативных гипотез  j = 1 ,.. m. Кроме того, значения критерия должны быть вычисляемы по наблюдаемой выборке
j = 1 ,.. m. Кроме того, значения критерия должны быть вычисляемы по наблюдаемой выборке 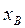 , т.е.
, т.е.  .
.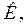 при которых гипотеза отвергается. Критическую область будем обозначать
при которых гипотеза отвергается. Критическую область будем обозначать 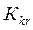 . Тогда решающее правило критерия проверки будет следующим:
. Тогда решающее правило критерия проверки будет следующим: отвергается (по наблюдаемой выборке),
отвергается (по наблюдаемой выборке),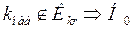 принимается (нет оснований отвергать гипотезу).
принимается (нет оснований отвергать гипотезу).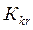 отделяется от области принятия гипотезы, называются критическими точками критерия
отделяется от области принятия гипотезы, называются критическими точками критерия 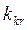 . Как построить критическую область критерия?
. Как построить критическую область критерия? должно иметь в рамках проверяемой гипотезы большую вероятность. В противном случае, если вероятность наблюдаемой величины мала, проверяемую гипотезу нужно отвергать в пользу иных альтернативных гипотез.
должно иметь в рамках проверяемой гипотезы большую вероятность. В противном случае, если вероятность наблюдаемой величины мала, проверяемую гипотезу нужно отвергать в пользу иных альтернативных гипотез.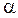 ошибки 1-го рода, как наиболее значимой. Исключить такую ошибку при проверке гипотезы невозможно (
ошибки 1-го рода, как наиболее значимой. Исключить такую ошибку при проверке гипотезы невозможно (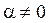 ), на практике обычно эту вероятность задают достаточно малой величиной
), на практике обычно эту вероятность задают достаточно малой величиной  ;
;  ;
; 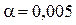 и называют уровнем значимости гипотезы.
и называют уровнем значимости гипотезы. ,
,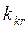 однозначно, то задача построения критической области критерия решена. В противном случае, когда ещё остаётся свобода выбора критических точек, рассмотрим влияние альтернативных гипотез. Поскольку величина
однозначно, то задача построения критической области критерия решена. В противном случае, когда ещё остаётся свобода выбора критических точек, рассмотрим влияние альтернативных гипотез. Поскольку величина  - есть вероятностьпринять неверную гипотезу
- есть вероятностьпринять неверную гипотезу  при условии справедливости альтернативной гипотезы
при условии справедливости альтернативной гипотезы 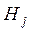 , то
, то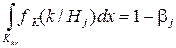
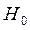 при условии справедливости
при условии справедливости 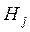 и её называют мощностью критерия по отношению к альтернативной гипотезе
и её называют мощностью критерия по отношению к альтернативной гипотезе  , критическую область критерия нужно строить так, чтобы мощность критерия была максимальной
, критическую область критерия нужно строить так, чтобы мощность критерия была максимальной 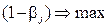 по отношению ко всем альтернативным гипотезам.
по отношению ко всем альтернативным гипотезам.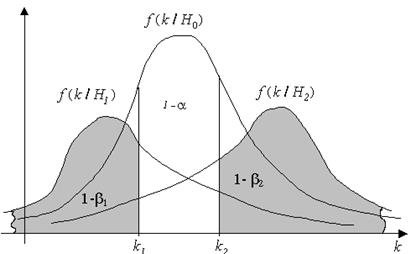
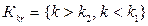 при наличии двух альтернативных гипотез
при наличии двух альтернативных гипотез 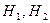
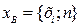 объёмом n, а проверяемой гипотезой является гипотеза о не грубой ошибке при измерении элемента
объёмом n, а проверяемой гипотезой является гипотеза о не грубой ошибке при измерении элемента  этой выборки. Тогда
этой выборки. Тогда 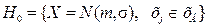 ,
, 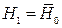 . Критерием для проверки гипотезы является величина Стьюдента
. Критерием для проверки гипотезы является величина Стьюдента .
.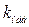 и критическую точку при заданном уровне значимости
и критическую точку при заданном уровне значимости 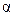 проверяемой гипотезы
проверяемой гипотезы  можно судить о грубости данного измерения. Обычно на грубость измерения проверяются крайние точки наблюдений (максимальная и минимальная). Проверим на грубость измеренную максимальную температуру в рассмотренной выше выборке майских температурных измерений.
можно судить о грубости данного измерения. Обычно на грубость измерения проверяются крайние точки наблюдений (максимальная и минимальная). Проверим на грубость измеренную максимальную температуру в рассмотренной выше выборке майских температурных измерений.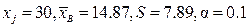 ,
,  ,
, 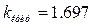
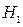 о грубости этого измерения. Таким образом, это измерение грубое и его лучше убрать из выборки. Вывод критерия зависит от точности измерения (её объёма n) и значимости гипотезы, то есть риска ошибиться при отклонении верной гипотезы. Так, если уровень значимости гипотезы повысить до 5%, то
о грубости этого измерения. Таким образом, это измерение грубое и его лучше убрать из выборки. Вывод критерия зависит от точности измерения (её объёма n) и значимости гипотезы, то есть риска ошибиться при отклонении верной гипотезы. Так, если уровень значимости гипотезы повысить до 5%, то 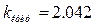 , то измерение уже не является грубым.
, то измерение уже не является грубым. равна нулю
равна нулю  , а в наблюдениях ее выборочный аналог
, а в наблюдениях ее выборочный аналог 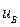 отличен от нуля. Действительно ли наблюдаемое значение не нулевое (значимое), или это произошло случайно на рассматриваемой выборке? Для ответа на этот вопрос очень часто в дальнейшем мы будем использовать критерий Стьюдента рис. 2.8 в виде:
отличен от нуля. Действительно ли наблюдаемое значение не нулевое (значимое), или это произошло случайно на рассматриваемой выборке? Для ответа на этот вопрос очень часто в дальнейшем мы будем использовать критерий Стьюдента рис. 2.8 в виде: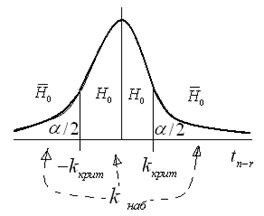
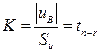 ,
,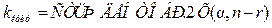
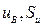 статистическая оценка и её несмещённая ошибка,
статистическая оценка и её несмещённая ошибка, 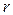 количество степеней свободы выборки, потерянных при построении оценки. Для удобства часто вводится понятие жёесткости критерия
количество степеней свободы выборки, потерянных при построении оценки. Для удобства часто вводится понятие жёесткости критерия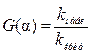 .
.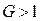 , когда проверяемая гипотеза о нулевом значении теоретической величины отвергается.
, когда проверяемая гипотеза о нулевом значении теоретической величины отвергается.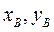 одинакового объёма.
одинакового объёма. ,
, 
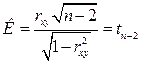 .
.
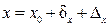 ,
, - истинное или среднее значение величины,
- истинное или среднее значение величины, 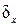 - флуктуация измеряемой величины,
- флуктуация измеряемой величины, 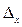 - ошибка измерительного прибора и измеряющего субъекта. Виды измерений разнообразны и классифицируются по множеству признаков (рис. 3.2).
- ошибка измерительного прибора и измеряющего субъекта. Виды измерений разнообразны и классифицируются по множеству признаков (рис. 3.2).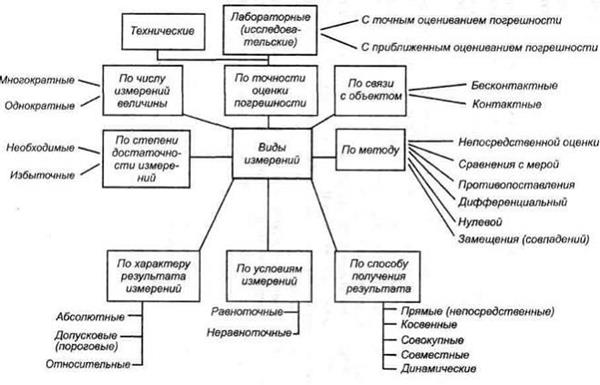
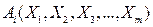 , измеряется (фиксируется) несколько величин-факторов
, измеряется (фиксируется) несколько величин-факторов  . Измерения могут проводиться как одновременно по n однотипным объектам (пространственные ряды данных), так и n измерений одного объекта в разные моменты времени (временные ряды данных) рис.3.3.
. Измерения могут проводиться как одновременно по n однотипным объектам (пространственные ряды данных), так и n измерений одного объекта в разные моменты времени (временные ряды данных) рис.3.3.
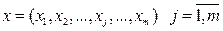 . Объединим все измерения ряда в матрицу измерений.
. Объединим все измерения ряда в матрицу измерений.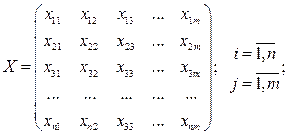
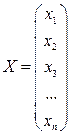 ;
; 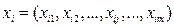

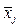 и среднеквадратические отклонения
и среднеквадратические отклонения  по каждому измеримому фактору, проведём центрирование и нормирование переменных
по каждому измеримому фактору, проведём центрирование и нормирование переменных 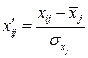 и тем самым приведём матрицу измерений к стандартному виду, в котором
и тем самым приведём матрицу измерений к стандартному виду, в котором 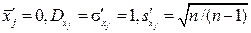 . Помимо единого масштаба для всех измеряемых факторов, такой вид матрицы измерения, как увидим далее, позволяет упростить ряд статистических формул. Поэтому в дальнейшем будем пользоваться именно стандартной формой матрицы измерений, а штрихи будем отпускать. При необходимости всегда можно пересчитать все получаемые величины в реальный масштаб по формуле
. Помимо единого масштаба для всех измеряемых факторов, такой вид матрицы измерения, как увидим далее, позволяет упростить ряд статистических формул. Поэтому в дальнейшем будем пользоваться именно стандартной формой матрицы измерений, а штрихи будем отпускать. При необходимости всегда можно пересчитать все получаемые величины в реальный масштаб по формуле  .
. - урожайность участка (кг/сотка)
- урожайность участка (кг/сотка)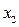 - экспертная оценка уровня инфраструктуры участка,
- экспертная оценка уровня инфраструктуры участка,


