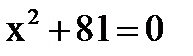Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Вычисление объема тела по известным площадям поперечных сечений
Если площадь сечения тела плоскостью, перпендикулярной оси Ох, может быть выражена как функция от х (в виде S=S(x)), то объем части тела, заключенной между перпендикулярными оси Ох плоскостями х=а, х=b, находится по формуле:
Вычисление объема тела вращения Если криволинейная трапеция ограничена кривой y=f(x) и прямыми х=а, х=b, вращается вокруг оси Ох, то объем тела вычисляется по формуле
Если криволинейная трапеция ограничена кривыми y1=f1(x), y2=f2(x) и прямыми х=а, х=b, вращается вокруг оси Ох, то объем тела вычисляется по формуле
Пример. Вычислите объем тела, образованного вращением фигуры, ограниченной линиями Решение Вычислим объём полученного тела по формуле:
Входной контроль 1.Запишите вычисление объема тела по известным площадям поперечных сечений 2.Запишите вычисление объема тела вращения Ход работы 1.Найдите объем тела, полученного вращением вокруг оси Ох фигуры, ограниченной кривой 2.Найти объем фигуры, полученной вращением части синусоиды, заключенной между точками, абсциссы которых 3. Найдите объем тела, полученного вращением вокруг оси Ох фигуры, ограниченной кривыми Выходной контроль 1 вариант 1.(3 балла) Вычислите объем тела, образованного вращением фигуры, ограниченной линиями 2. (4 балла) Найти объем фигуры, полученной вращением части косинусоиды, заключенной между точками, абсциссы которых 3.(4 балла) Найдите объем тела, полученного вращением вокруг оси Ох фигуры, ограниченной кривыми 2 вариант 1.(3 балла) Вычислите объем тела, образованного вращением фигуры, ограниченной линиями 2.(4 балла) Найти объем фигуры, полученной вращением части косинусоиды, заключенной между точками, абсциссы которых 3.(4 балла) Найдите объем тела, полученного вращением вокруг оси Ох фигуры, ограниченной кривыми Критерии оценки:
Практическое занятие № 18 Тема: Приближённое вычисление определённого интеграла
Цель: Научиться приближённо вычислять определённые интегралы Теоретические основы При решении физических и технических задач приходится находить определенные интегралы от функций, первообразные которых не выражаются через элементарные функции. Это привело к необходимости вывода приближенных формул вычисления определенных интегралов. Для приближённого вычисления интеграла функции f(x) используются методы приближённого интегрирования, наиболее употребительные из них основаны на замене интеграла конечной суммой. Формула прямоугольников Допустим, что где
Погрешность формулы: где k -наибольшее значение Относительную погрешность вычисления по формуле прямоугольников можно определить по формуле:
Формула трапеций. Пусть требуется вычислить интеграл Где f(xk-1) и f(xk) - соответственно основания трапеций; xk - xk-1 = (b-a)/n - их высоты. Таким образом, получена приближенная формула
Если функция f(x) имеет на [a, b] непрерывную вторую производную, то абсолютная величина погрешности формулы трапеций не больше, чем где k -наибольшее значение
Вычислим теперь по формуле трапеций его приближенное значение. Пусть n=5. Тогда имеем: a=x0=0, x1=0,2, x2=0,4, x3=0,6, x4=0,8, x5=1=b и соответственно f(x0)=0, f(x1)=0,04, f(x2)=0,16, f(x3)=0,36, f(x4)=0,64, f(x5)=1. Следовательно,
Точное значение интеграла равно 0,3333...., поэтому абсолютная ошибка меньше 0,007. Во многих технических задач эта точность достаточна. Если увеличить число n, то точность будет большей. Так, например, при n=10
т.е. абсолютная ошибка меньше 0,002. Формула Cимпсона
Эта формула называется формулой парабол или формулой Симпсона. В формуле параболы значение функции f(x) в нечетных точках разбиения х1, х3,..., х2n-1 имеет коэффициент 4, в четных точках х2, х4,..., х2n-2 - коэффициент 2 и в двух граничных точках х0=а, х1, х2n =b - коэффициент 1. Геометрический смысл формулы Симпсона очевиден: площадь криволинейной трапеции под графиком функции f(x) на отрезке [a, b] приближенно заменяется суммой площадей фигур, лежащих под параболами (прямыми).
Если функция f(x) имеет на [a, b] непрерывную вторую производную, то абсолютная величина погрешности формулы Симпсона не больше, чем где k -наибольшее значение Для сравнения точности приближенных формул вычислим еще раз интеграл
По формуле Симпсона получаем
Входной контроль: 1. Для чего используется численное интегрирование? 2. Запишите формулу для вычисления определенного интеграла методом прямоугольников 3. Запишите формулу для вычисления определенного интеграла методом трапеций 4. Рассматривая геометрический смысл формул прямоугольников, трапеций сформулируйте их отличие друг от друга Ход работы: 1. Вычислите определенный интеграл по формуле прямоугольников 2. Вычислите определенный интеграл по формуле трапеций 3. Вычислите определенный интеграл по формуле Симпсона Выходной контроль Каждое задание -2 балла 1 вариант 1.Вычислите определенный интеграл по формуле прямоугольников. 2.Вычислите определенный интеграл по формуле трапеций 3.Вычислите определенный интеграл по формуле Симпсона 2 вариант 1.Вычислите определенный интеграл по формуле прямоугольников. 2.Вычислите определенный интеграл по формуле трапеций Вычислите определенный интеграл по формуле трапеций 3. Вычислите определенный интеграл по формуле Симпсона Критерии оценки:
Практическое занятие № 19 Тема: Действия над комплексными числами в алгебраической форме Цель: Научиться выполнять действия над комплексными числами в алгебраической форме Теоретические основы Комплексным числом называется выражение вида: z=a+biгде а- действительная часть комплексного числа, b- мнимая часть комплексного числа.
1.Существует элемент i (мнимая единица) такой, что i2 = – 1. 2. Символ a + bi называют комплексным числом с действительной частью a и мнимой частью bi, где a и b – действительные числа, b – коэффициент мнимой части. Комплексное число a + 0i отождествляется с действительным числом a, т.е. a + 0i = a, в частности, 0 + 0i = 0. Числа вида bi (b № 0) называют чисто мнимыми. Например, комплексное число 2 + 3i имеет действительную часть – действительное число 2 и мнимую часть 3i, действительное число 3 – коэффициент мнимой части. Комплексное число 2 – 3i имеет действительную часть число 2, мнимую часть – 3i, число – 3 – коэффициент при мнимой части. 3. Правило равенства. Два комплексных числа равны тогда и только тогда, когда равны их действительные части и равны коэффициенты мнимых частей. Т.е., если a + bi = c +di, то a = c, b = d: и, обратно, если a = c, b = d, то a + bi = c +di. 4. Правило сложения и вычитания комплексных чисел. (a + bi) + (c + di) = (a + c) + (b + d)i. Например: (2 + 3i) + (5 + i) = (2 + 5) + (3 + 1)i = 7 + 4i; (– 2 + 3i) + (1 – 8i) = (– 2 + 1) + (3 + (– 8))i = – 1 – 5i; (– 2 + 3i) + (1 – 3i) = (– 2 + 1) + (3 + (– 3))i = – 1 + 0i = – 1. Вычитание комплексных чисел определяется как операция, обратная сложению, и выполняется по формуле: (a + bi) – (c + di) = (a – c) + (b – d)i. Например: (5 – 8i) – (2 + 3i) = (3 – 2) + (– 8 – 3)i = 1 – 11i; (3 – 2i) – (1 – 2i) = (3 – 1) + ((– 2) – (– 2))i = 2 + 0i = 2. 5. Правило умножения комплексных чисел. (a + bi)(c + di) = (aс + bd) + (ad + bc)i. Из определений 4 и 5 следует, что операции сложения, вычитания и умножения над комплексными числами осуществляются так, как будто мы выполняем операции над многочленами, однако с условием, что i2 = – 1. Действительно: (a + bi)(c + di) = ac + adi + bdi2 = (ac – bd) + (ad + bc)i. Например, (– 1 + 3i)(2 + 5i) = – 2 – 5i + 6i + 15i2 = – 2 – 5i + 6i – 15 = – 17 + i; (2 + 3i)(2 – 3i) = 4 – 6i + 6i – 9i2 = 4 + 9 = 13. 6. Деление комплексного числа a + bi на комплексное число c + di № 0 определяется как операция обратная умножению и выполняется по формуле:
Формула теряет смысл, если c + di = 0, так как тогда c2 + d2 = 0, т. е. деление на нуль и во множестве комплексных чисел исключается. Обычно деление комплексных чисел выполняют путем умножения делимого и делителя на число, сопряженное делителю. Входной контроль 1. Дайте определение комплексного числа 2. В чем заключаются действия над комплексными числами в алгебраической форме? Ход работы 1.Решите квадратные уравнения: 1) 2.Изобразите комплексные числа на координатной плоскости:
z 1 =-1+ i z 2 =-1- i z 3 =7 i z 4 =-5 3.Выполнить сложение, вычитание, умножение и деление комплексных чисел заданных в алгебраической форме 1) Выходной контроль 1 вариант 1.Решите квадратные уравнения: 1) (1 балл) 2.Изобразите комплексные числа на координатной плоскости: 1) (1 балл) z=3+i 2) (1 балл) z=-4+i 3) (1 балл) z=-i 4) z=7 3.Выполнить сложение(1 балл), вычитание(1 балл), умножение(2 балла) и деление(3 балла) комплексных чисел заданных в алгебраической форме z 1 =5- i и z 2 =2+4 i 2 вариант 1.Решите квадратные уравнения: 1) (1 балл) 2.Изобразите комплексные числа на координатной плоскости: 1)(1 балл) z=2+5i 2) (1 балл) z=7-i 3) (1 балл) z=3i 4) (1 балл) z=5 3.Выполнить сложение(1 балл), вычитание(1 балл), умножение(2 балла) и деление (3 балла) комплексных чисел заданных в алгебраической форме z 1 =1+3 i и z 2 =1-6 i Критерии оценки:
Практическое занятие № 20 Тема: Действия над комплексными числами в тригонометрической форме Цель: Научиться выполнять действия над комплексными числами в тригонометрической форме Теоретические основы
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2020-11-11; просмотров: 737; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.138.174.195 (0.065 с.) |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
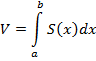
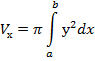
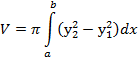
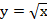 , у=0, х=3
, у=0, х=3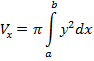
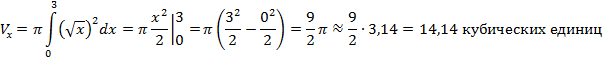
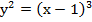 и прямой х=2
и прямой х=2 ,
, 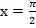
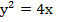 и
и 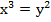
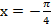 ,
, 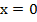
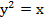 и
и 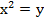
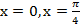 ,
,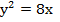 и
и 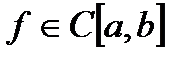 Положим приближенно
Положим приближенно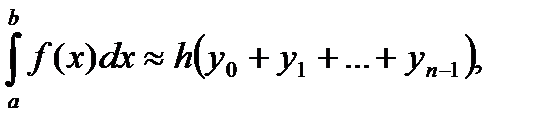 высотой является левая ордината,
высотой является левая ордината,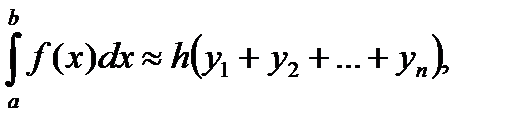 высотой является правая ордината,
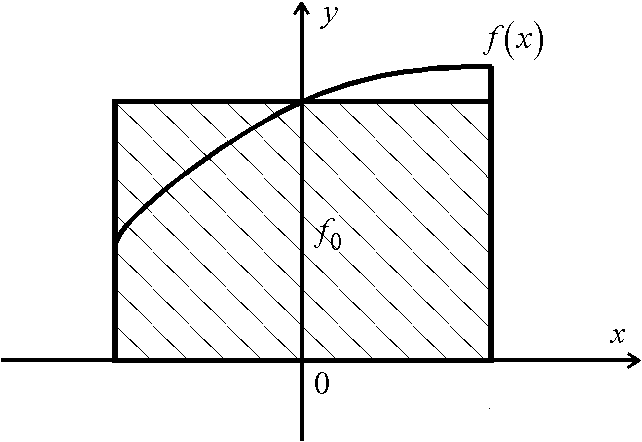
высотой является правая ордината,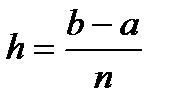 , т.е. площадь криволинейной трапеции, ограниченной сверху графиком функции
, т.е. площадь криволинейной трапеции, ограниченной сверху графиком функции 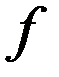 , аппроксимируется (заменяется)площадью прямоугольника, высота которого равна значению
, аппроксимируется (заменяется)площадью прямоугольника, высота которого равна значению 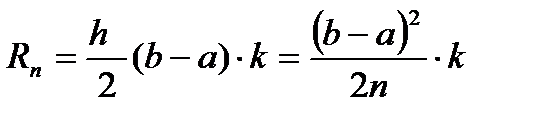 ,
, 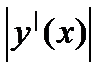 на отрезке [a, b]. а<х< b
на отрезке [a, b]. а<х< b ;
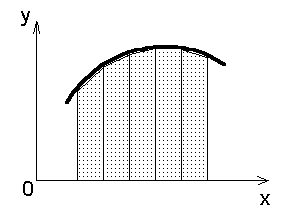
; , где f(x) - непрерывная функция. Для простоты рассуждений ограничимся случаем, когда f(x)³0. Разобьем отрезок [a, b] на n отрезков точками a=x0<x1<x2<...<xk-1<xk<...<xn=b и с помощью прямых х=хk построим n прямолинейных трапеций (эти трапеции заштрихованы на рис. 1). Сумма площадей трапеций приближенно равна площади криволинейной трапеции, т.е.
, где f(x) - непрерывная функция. Для простоты рассуждений ограничимся случаем, когда f(x)³0. Разобьем отрезок [a, b] на n отрезков точками a=x0<x1<x2<...<xk-1<xk<...<xn=b и с помощью прямых х=хk построим n прямолинейных трапеций (эти трапеции заштрихованы на рис. 1). Сумма площадей трапеций приближенно равна площади криволинейной трапеции, т.е.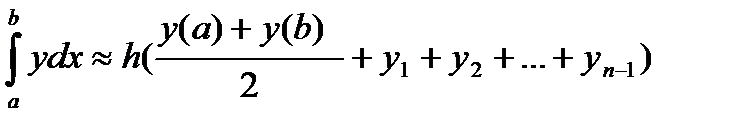 , которая и называется формулой трапеций. Эта формула тем точнее, чем больше n.
, которая и называется формулой трапеций. Эта формула тем точнее, чем больше n.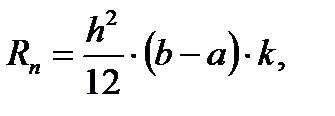
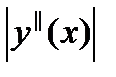 на отрезке [a, b]. а<х< b Пример1 Вычислить интеграл
на отрезке [a, b]. а<х< b Пример1 Вычислить интеграл  Точное значение этого интеграла находится просто:
Точное значение этого интеграла находится просто: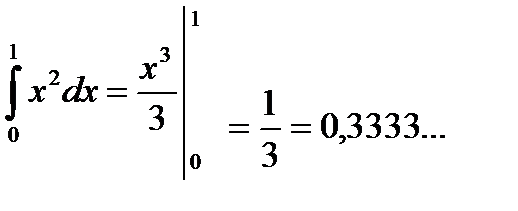
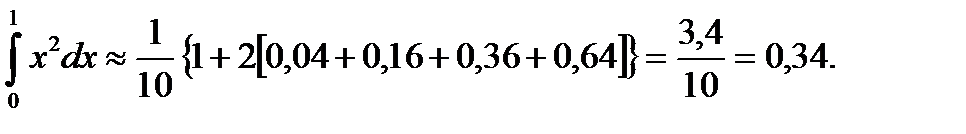
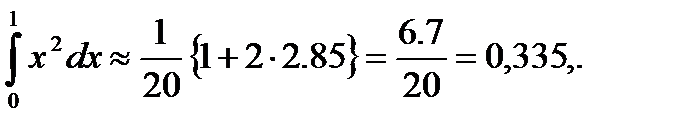
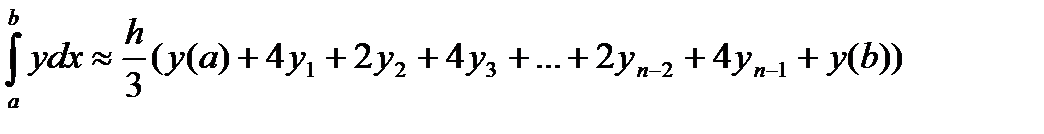


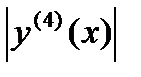 на отрезке [a, b]. а<х< b
на отрезке [a, b]. а<х< b , но теперь по формуле Симпсона при n=4. Разобьем отрезок [0, 1] на четыре равные части точками х0=0, х1=1/4, х2=1/2, х3=3/4, х4=1 и вычислим приближенно значения функции f(x)=1/(1+x) в этих точках у0=1,0000, у1=0,8000, у2=0,6667, у3=0,5714, у4=0,5000.
, но теперь по формуле Симпсона при n=4. Разобьем отрезок [0, 1] на четыре равные части точками х0=0, х1=1/4, х2=1/2, х3=3/4, х4=1 и вычислим приближенно значения функции f(x)=1/(1+x) в этих точках у0=1,0000, у1=0,8000, у2=0,6667, у3=0,5714, у4=0,5000.
 , разбив интервал интегрирования на 10 частей.
, разбив интервал интегрирования на 10 частей.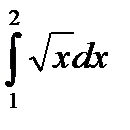 при n =5.
при n =5.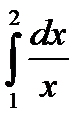 при n =5.
при n =5.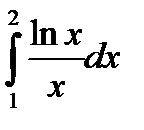 при n =10.
при n =10.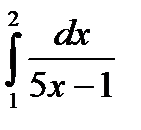 при n =10.
при n =10.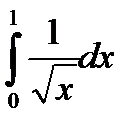 при n =5.
при n =5. при n =8.
при n =8. при n =10.
при n =10.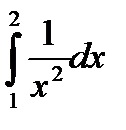 при n =5.
при n =5.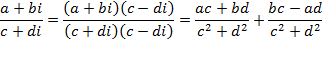
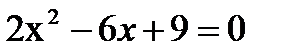 2)
2) 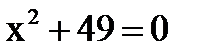 3)
3) 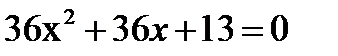
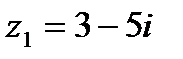
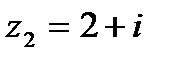 2) z 1 =7+2 i и z 2 =3+7 i
2) z 1 =7+2 i и z 2 =3+7 i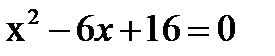 2) (1 балл)
2) (1 балл) 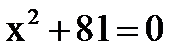
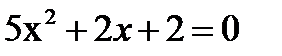 2) (1 балл)
2) (1 балл)