Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Интегрирование подстановкой (замена переменной)
Формулы интегрирования справедливы и в том случае, если переменная интегрирования является в свою очередь функцией от какой-либо другой переменной. На этом важном свойстве интегралов основан так называемый способ подстановки (метод замены переменной интегрирования). При интегрировании подстановкой следует ввести новую переменною с тем расчётом, чтобы получить один из табличных интегралов. В полученной первообразной функции необходимо вернутся к «старой» переменной интегрирования. Пример Найти интеграл Решение:
Интегрирование по частям Заключается в применении формулы Данный метод применим в том случае, если задача нахождения указанных двух интегралов более проста, чем нахождение заданного интеграла. Причем, 1. В интегралах вида 2. В интегралах вида 3. В интегралах вида Если существует конечный передел интегральной суммы
при λ→0, не зависящий от способа разбиения τn отрезка [a; b] на частичные отрезки и выбора промежуточных точек ξk, то этот предел называют определенным интегралом (или интегралом Римана) от функции f(x) на отрезке [a; b] и обозначают:
Если указанный предел существует, то функция f(x) называется интегрируемой на отрезке [a; b] (или интегрируемой по Риману). При этом f(x)dx называется подынтегральным выражением, f(x) – подынтегральной функцией, х – переменной интегрирования, a и b – соответственно нижним и верхним пределами интегрирования. Определенный интеграл есть число, равное пределу, к которому стремится интегральная сумма, в случае, когда диаметр разбиения λ стремится к нулю. Вычисление определенного интеграла основывается на формуле Ньютона-Лейбница:
Входной контроль 1. В чем заключается интегрирование заменой переменной 2. Запишите формулу интегрирования по частям Ход работы 1. 2. 3. 4. 5. 6. Выходной контроль 1 вариант 1.(3 балла) 2. (3 балла) 3. (4 балла) 4. (4 балла) 2 вариант 1. (3 балла) 2. (3 балла) 3. (4 балла) 4. (4 балла) Критерии оценки:
Практическое занятие № 16 Тема: Вычисление площадей Цель: Научиться вычислять площади фигур Теоретические основы Пусть на отрезке [а,b] оси Ох задана непрерывная функция f, не меняющая на нем знака. Фигуру, ограниченную графиком > функции У =f(x) на отрезком [а,b]н прямыми х-а, х = b, называют
3)
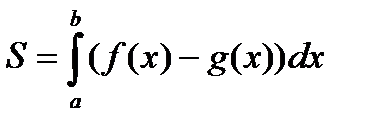
Входной контроль
Ход работы Найти площадь фигуры, ограниченной графиками функции: 1) y=cosx, y=0, x=0, x= 2) y = -х2 + 4, у = 0 3) у = 4) 5) Выходной контроль Вычислить площадь фигуры, ограниченной графиками функции- каждое задание -3 балла Вариант1 Вариант 2 1. 2. 3. Критерии оценки:
Практическое занятие № 17 Тема: Вычисление объёмов тел вращения
Цель: Научиться вычислять объёмы тел вращения Теоретические основы
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2020-11-11; просмотров: 199; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.52.86 (0.011 с.) |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

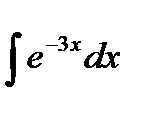
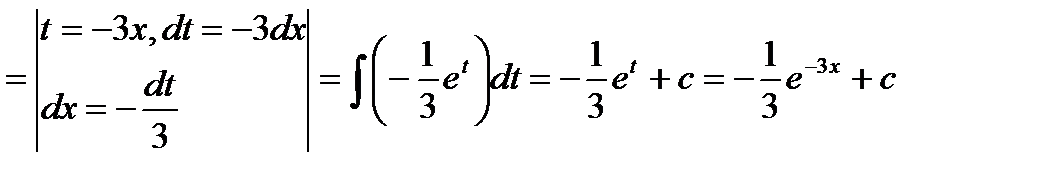
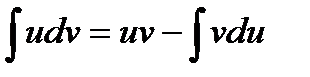
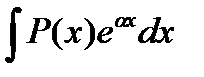 ,
,  ,
, 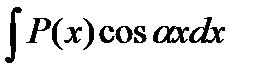 Заменяют
Заменяют 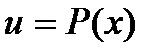
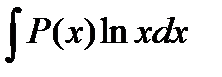 ,
, 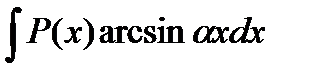 ,
,  Заменяют
Заменяют 
 ,
, 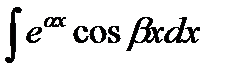 , Заменяют за u любую из функций. Интегрирование по частям применяется несколько раз.
, Заменяют за u любую из функций. Интегрирование по частям применяется несколько раз.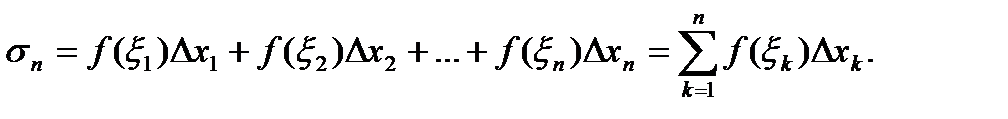
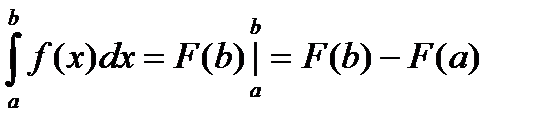
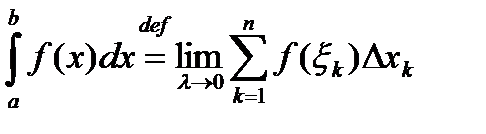


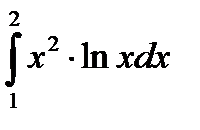
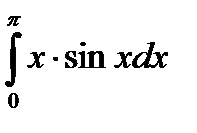
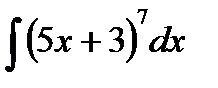
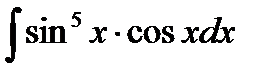
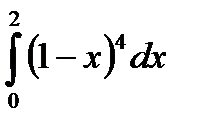
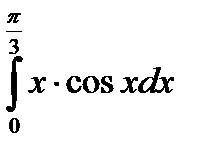
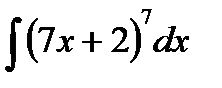



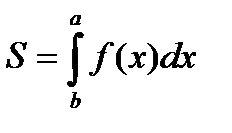 Площадь криволинейной трапеции находится по формуле:
Площадь криволинейной трапеции находится по формуле: 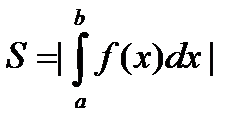
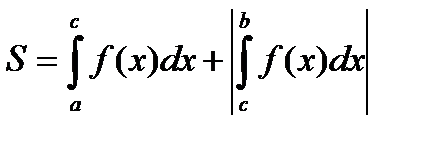
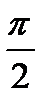
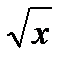 , у = 0, х = 4, х = 9
, у = 0, х = 4, х = 9
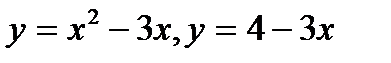
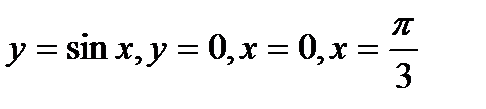 1.
1. 
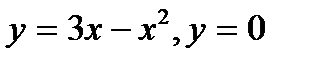 2.
2. 
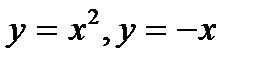 3.
3.