Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Физический смысл производной.
Если точка движется вдоль оси х и ее координата изменяется по закону x(t), то мгновенная скорость точки: v(t)= x|(t) Входной контроль 1 В чем заключается решение прикладных задач при помощи производной 2 В чем заключается физический смысл производной 3В чем заключается геометрический смысл производной Ход работы 1.Найдите скорость износа оборудования за период равный 5лет, если его износ изменяется по закону: 2. Заряд, протекающий через проводник, меняется по закону 3.Тело, масса которого равна 0,2 кг движется прямолинейно по закону 4.Найдите величину силы F, действующей на точку массой 0,1 кг, движущуюся по закону: Выходной контроль Каждая задача -2 балла 1 вариант 1.Заряд, протекающий через проводник, меняется по закону 2.Точка движется прямолинейно по закону 3.Точка движется прямолинейно по закону 4.Тело, масса которого равна 0,11 кг движется прямолинейно по закону 2 вариант 1.Изменение силы тока в зависимости от времени задано уравнением I = 2 t2 – 5 t. Найти скорость изменения силы тока в момент времени 10 с. 2.Точка движется прямолинейно по закону 3.Закон прямолинейного движения тела задан уравнением 4.Найдите величину силы F, действующей на точку массой 0,2 кг, движущуюся по закону: Критерии оценки:
Практическое занятие № 7 Тема: Приложение дифференциала к приближённым вычислениям Цель: Научиться применять дифференциал к приближённым вычислениям Теоретические основы Пусть функция y = f(х) дифференцируема на отрезке [a, b], содержащем некоторую точку x. Тогда производная в этой точке x определятся равенством
где α(Δx) – б.м.ф. при то есть приращение ∆у функции f(х), дифференцируемой в точке х, можно представить в виде суммы двух слагаемых, которые являются бесконечно малыми:
и α(Δx)· Δx – нелинейного члена. Первое слагаемое Определение. Главная часть приращения функции f(х), линейная относительно приращения независимой переменной ∆х, называется дифференциалом функции f(х) в точке х, т.е. это произведение производной f'(x) на приращение независимой переменной ∆х: dy =df(x)=f'(х)·∆х. Замечание 1. Дифференциал функции составляет основную (главную) часть ее приращения, линейную относительно ∆х. Например, приращение функции у = х2 в точке х = 1, вызванное приращением аргумента dх = 0,1, есть величина ∆у = (х + ∆х)2 – х2 = (1 + 0,1)2 – 12 = 0,21. Дифференциал функции в этой точке равен dy = f'(х) · ∆х = 2 · х · ∆х = 2 · 1 · 0,1 = 0,2. Таким образом, на нелинейную часть приращения α(Δx) · ∆х приходится величина 0,01 из полной величины приращения 0,21. Замечание 2. Дифференциал аргумента совпадает с его приращением (dх=∆х), поэтому дифференциал функции записывается в виде dy = df(х) = f'(x) dx, т.е. дифференциал функции равен произведению производной этой функции на дифференциал независимой переменной. Геометрический смысл дифференциала: dy = KN, т.е. дифференциал функции f(х) в точке x равен приращению ординаты касательной к графику функции в этой точке, когда x получит приращение Dх.
Дифференциал к приближённым вычислениям применяется по формуле:
Пример 1. Вычислить приближенное значение корня Решение. Рассмотрим функцию ∆х = 1-0,07=0,07, получим из формулы:
Пример 2. Найти приближенно sin310. Решение. Пусть x=310, x0=300 тогда ∆х =310-300=10 Перейдем из градусной меры угла в радианную: f(x)= sinx, тогда
f(300)= sin300=0,5;
Используя формулу получим:
Входной контроль 1. Дайте определение дифференциала функции 2. Запишите формулу применения дифференциала в приближенных вычислениях
Ход работы 1.Найдите дифференциал функции: 1) y= 2.Вычислите приближенно:
Выходной контроль 1 вариант 1.Найдите дифференциал функции (каждое задание-1 балл): 1) y=x4+6x+7 2) y= 2.Вычислите приближенно (каждое задание-3 балла): 1) 2 вариант 1.Найдите дифференциал функции (каждое задание-1 балл): 1) y=x5-3x+11 2) y= 2.Вычислите приближенно (каждое задание-3 балла): 1) Критерии оценки:
Практическое занятие № 8 Тема: Исследование функции. Построение графиков Цель: Научиться исследовать функции. Строить графики. Теоретические основы План исследования функции и построения ее графика 1. Область определения. 2. Четность, нечетность. 3. Производная. 4. Стационарные и критические точки. 5. Знаки производной, промежутки монотонности. 6. Экстремумы функции. 7. Точки пересечения с осями координат 8. График. Пример.
а) Функция определена для всех б) в) г) - 0 + 2 -
х=0 точка min; x=2 точка max;
убывает при д) Найдём экстремумы функции:
е) Найдём пересечение с осью Ох, для этого решим уравнение:
Построим график. у
Входной контроль 1. Запишите план исследования функции и построения ее графика. Ход работы Постройте графики функций
Выходной контроль Постройте графики функций 1 вариант 1) (7 баллов) у=х3-12х2+36х 2 вариант 1) (7 баллов) у=х3-6х2 Критерии оценки:
Практическое занятие № 9 Тема: Решение прикладных задач с помощью производной и дифференциала Цель: Научиться решать прикладные задачи с помощью производной и дифференциала Теоретические основы Решение прикладных задач посредством математики, как правило, содержит три основных этапа: 1) формализацию (перевод исходной задачи на язык математики), 2) решение полученной математической задачи, 3) интерпретация найденного решения («перевод» его с языка математики в терминах первоначальной задачи). Решение разнообразных прикладных задач часто сводится к нахождению дифференциала функции. Для решения данных задач используем схему: 1) задача переводится на язык функций. Для этого выбирают удобный параметр х, через который интересующую нас величину выражают как функцию f(x), 2) средствами анализа ищется приближенное значение этой функции с использованием дифференциала, 3)выясняется, какой практический смысл (в терминах первоначальной задачи) имеет полученный на языке функций) результат.
Формула нахождения приближенного значения функции с использованием дифференциала: Пример. Вычислите приближённо объём сферического слоя, если известно, что радиус внутренней поверхности R=0,5 м, а толщина равна 0,1 м Решение
Объём шара равен Объём сферического слоя есть приращение объёма шара, вызванное изменением радиуса от 0,5 до 0,6 м. Приращение объёма шара заменяем дифференциалом:
Подставим числовые значения R=0,5; dR=0,1 Имеем:
Решение разнообразных прикладных задач часто сводится к нахождению наибольшего и наименьшего значений функции. Для решения данных задач используем схему: 1) задача переводится на язык функций. Для этого выбирают удобный параметр х, через который интересующую нас величину выражают как функцию f(x), 2) средствами анализа ищется наибольшее или наименьшее значение этой функции на некотором промежутке, 3)выясняется, какой практический смысл (в терминах первоначальной задачи) имеет полученный на языке функций) результат. Правило для нахождения наибольшего и наименьшего значения функции на отрезке. 1) Нахождение производной функции 2) Нахождение критических точек (точек, в которых производная функции равна нулю или не существует) 3) Нахождение значений функции в концах отрезка и критических точках, принадлежащих данному отрезку. Пример Найдите наибольший объём цилиндра, вписанного в данный конус
Решение Пусть задан конус с высотой H и радиусом R. Обозначим через h высоту цилиндра и через r радиус основания цилиндра, вписанного в данный конус. Обозначим BM=x. Тогда
Объём цилиндра равен
Определим, при каком значении х объём цилиндра будет принимать наибольшее значение. Най дём производную:
Найдем критические точки: + -
0 Следовательно, в точке Входной контроль 1.Перечислите этапы решения прикладных задач 2.Запишите схему применения дифференциала для решения прикладных задач 3. Запишите формулу нахождения приближенного значения функции с использованием дифференциала, 4.Запишите схему применения производной для решения прикладных задач 5.Запишите правило нахождения наибольшего и наименьшего значений функции на отрезке Ход работы 1.Найти наименьшее и наибольшее значения функции y=x4-2x2+3 на отрезке [-3,2] 2.Объем продукции, произведенной бригадой рабочих, может быть описан уравнением
3.Электронагревательный прибор потребляет мощность от источника тока, э.д.с. которого равна E, а внутреннее сопротивление и сопротивление подводящих проводов в сумме равны r. Какое сопротивление R должен иметь прибор, чтобы в нем выделялась максимальная мощность? 4.На какой высоте над центром круглого стола радиуса 0,75м следует поместить лампочку, чтобы освещенность края стола была наибольшей? Яркость освещения выражается формулой E Выходной контроль 1 вариант 1.(3 балла) Найти наименьшее и наибольшее значения функции y=3x5-5x3 на отрезке [-2,3] 2. (3 балла) Объем продукции, произведенной бригадой рабочих, может быть описан уравнением
2 вариант 1.(3 балла) Найти наименьшее и наибольшее значения функции y=x4-8x2-9 на отрезке [-1,1] 2. (3 балла) Объем продукции, произведенной бригадой рабочих, может быть описан уравнением
Критерии оценки:
Практическое занятие № 10
Тема: Вычисление пределов функций в точке и на бесконечности Цель: Научиться вычислять пределы функций в точке и на бесконечности Теоретические основы: Определение: Число в называется пределом функции Смысл выражения Приведём без доказательства основные теоремы о пределах функций.
Предел отношения двух функций равен отношению пределов этих функций, если только предел делителя не равен нулю. Первый замечательный предел Второй замечательный предел Пример. 1)
2) Входной контроль: 1.Запишите формулы первого замечательного предела 2.Запишите формулы второго замечательного предела Ход работы: 1.Вычислите предел: а) 2.Вычислите предел: а) 3.Вычислите предел: а) Выходной контроль Вычислите пределы функций: 1 вариант 1) (1балл) 2) (1балл) 3) (2балла) 4) (1балл) 5) (3балла)
2 вариант 1) (1балл) 2) (1балл) 3) (1балл) 4) (2балла) 5) (3балла)
Критерии оценки:
Практическое занятие № 11 Тема: Дифференцирование сложных функций. Цель: Научиться находить производные сложных функций. Теоретические основы Производная. Пусть
Производной функции Обозначение:
функция, имеющая производную в точке х, называется дифференцируемой в этой точке; операция нахождения производной называется дифференцированием. Функция, дифференцируемая в каждой точке некоторого интервала, называется дифференцируемой на этом интервале. Производная элементарных функций.
Правила дифференцирования.
Производная сложной функции. Если у есть функция от u:
Производная сложной функции равна произведению её производной по промежуточному аргументу на производную этого аргумента по независимой переменной. Входной контроль 1.Определение производной 2.Таблица производной элементарных функций 3.Формулы дифференцирования 4.Производная сложной функции Ход работы Найти производные сложных функций.
Выходной контроль Найдите производные функций (каждое задание -2 балла) 1 вариант 1) 2) 3) 4) 5) 2 вариант 1) 2) 3) 4) 5) Критерии оценки:
Практическое занятие № 12 Тема: Нахождение частных производных Цель: Научиться находить частные производные Теоретические основы Определение 1. Функцией двух переменных называется функция вида: z=f(x,y) Определение 2. Функцией трех переменных называется функция вида: F=f(x,y,z) Определение 3. Функцией нескольких переменных называется функция вида: F=f(x,y,z,…)
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2020-11-11; просмотров: 318; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.17.203.68 (0.161 с.) |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
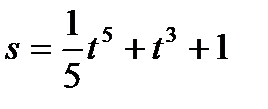
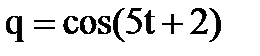 . Найти силу тока и скорость изменения силы тока в момент времени t=
. Найти силу тока и скорость изменения силы тока в момент времени t= 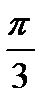 c
c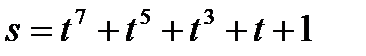 . Найдите кинетическую энергию тела через три секунды после начала движения.
. Найдите кинетическую энергию тела через три секунды после начала движения.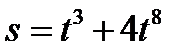 , при t =1 c
, при t =1 c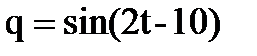 . Найти силу тока в момент времени t=5 c.
. Найти силу тока в момент времени t=5 c.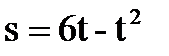 . Найти момент времени, при котором скорость точки окажется равной нулю.
. Найти момент времени, при котором скорость точки окажется равной нулю.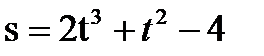 . Найти ускорение в момент времени t=4 c.
. Найти ускорение в момент времени t=4 c. . Найдите кинетическую энергию тела через две секунды после начала движения.
. Найдите кинетическую энергию тела через две секунды после начала движения.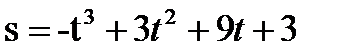 . Найти максимальную скорость движения тела.
. Найти максимальную скорость движения тела.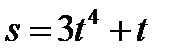 , при t =2 c
, при t =2 c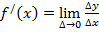 . Из этого равенства (по теореме о связи функции, ее предела и бесконечно малой функции) следует, что
. Из этого равенства (по теореме о связи функции, ее предела и бесконечно малой функции) следует, что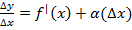 ,
,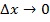 . Отсюда
. Отсюда 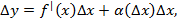
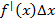 – линейного члена относительно Δx
– линейного члена относительно Δx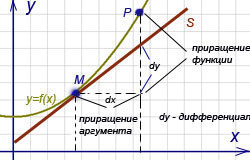
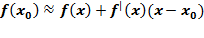 , где
, где 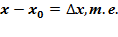
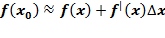
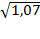 .
.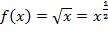 в окрестности точки x =1.Найдем производную функции
в окрестности точки x =1.Найдем производную функции 
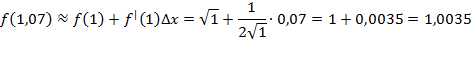
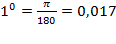
 значит:
значит: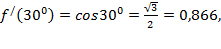
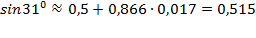
 x3-2x+5 2) y=
x3-2x+5 2) y= 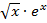 3) y=
3) y= 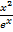 4)y=sin(5x-7)
4)y=sin(5x-7)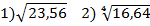 3)
3)  4) tg
4) tg 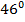 5) cos
5) cos  6) ln 0,998
6) ln 0,998 3) y=
3) y= 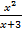 4)y=tg(1-x)
4)y=tg(1-x)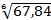 , 2) 2)
, 2) 2) 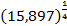 , 3)
, 3) 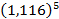 , 4) sin
, 4) sin 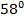 , 5) ln1,233
, 5) ln1,233 3) y=
3) y=  4)y=ctg(8-x)
4)y=ctg(8-x) )
)  , 4) sin
, 4) sin 

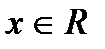 , непрерывна.
, непрерывна.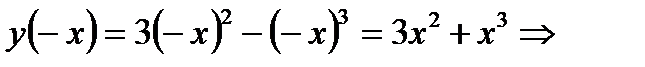 ни чётная, ни нечётная.
ни чётная, ни нечётная.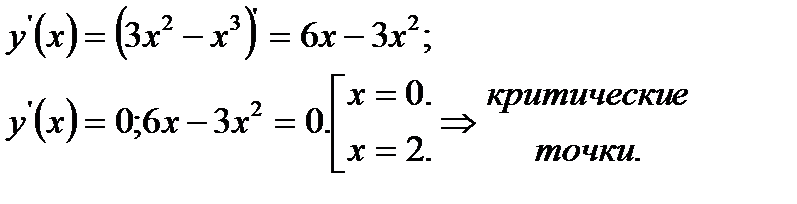
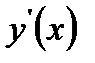
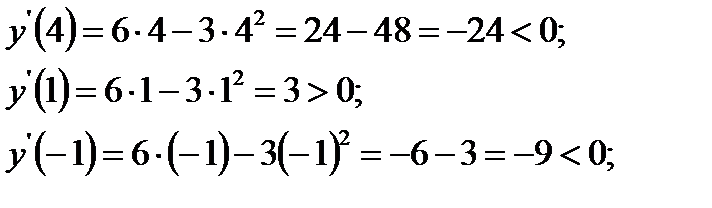
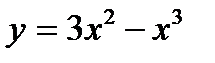 возрастает при
возрастает при 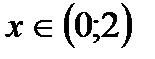
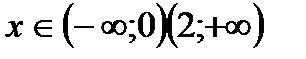
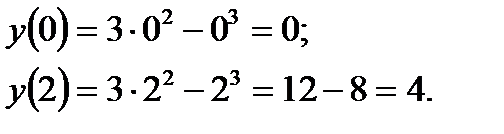
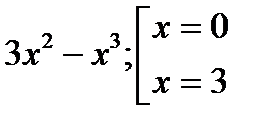
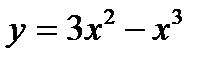
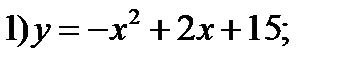

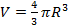
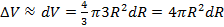
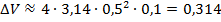
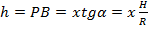 и r=R-x
и r=R-x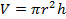 подставим и получим
подставим и получим
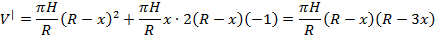
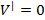 при
при 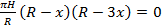 . Решая полученное уравнение получим:
. Решая полученное уравнение получим: 
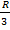
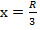 функция имеет максимум, то
функция имеет максимум, то 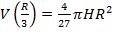 является наибольшим значением объёма вписанных цилиндров.
является наибольшим значением объёма вписанных цилиндров. 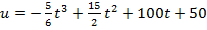 (ед), 0
(ед), 0 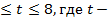 рабочее время в часах. Вычислить производительность труда и скорость через час после начала работы и до ее окончания.
рабочее время в часах. Вычислить производительность труда и скорость через час после начала работы и до ее окончания.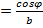 , где b– расстояние от источника света до освещаемой площадки.
, где b– расстояние от источника света до освещаемой площадки.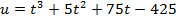 (ед),
(ед),  рабочее время в часах. Вычислить производительность труда и скорость через три часа после начала работы и до ее окончания.
рабочее время в часах. Вычислить производительность труда и скорость через три часа после начала работы и до ее окончания.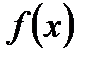 при
при 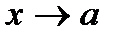 ; если для любого положительного числа Е можно указать такой интервал, содержащий точку
; если для любого положительного числа Е можно указать такой интервал, содержащий точку 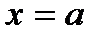 будет выполняться
будет выполняться 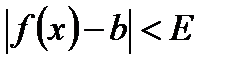 .
. заключается в следующем: если значения аргумента выбираются всё ближе и ближе к значению
заключается в следующем: если значения аргумента выбираются всё ближе и ближе к значению 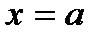 , то значения функции всё меньше и меньше отличаются от предельного значения в.
, то значения функции всё меньше и меньше отличаются от предельного значения в.


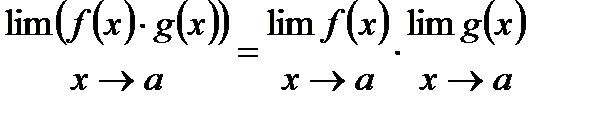
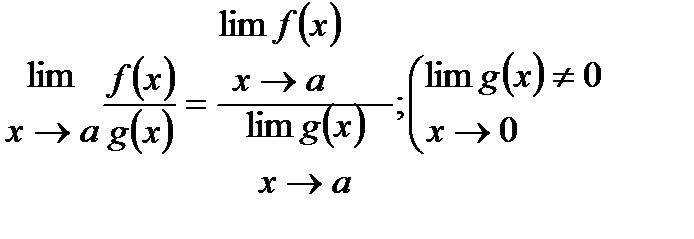
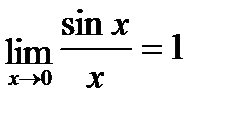
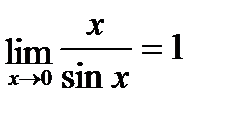
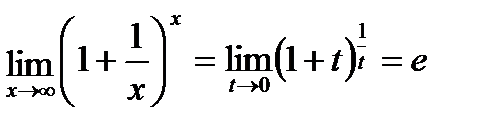
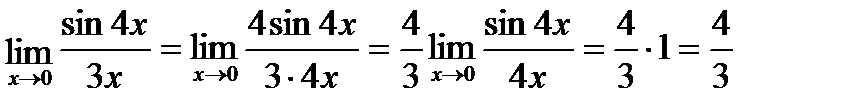
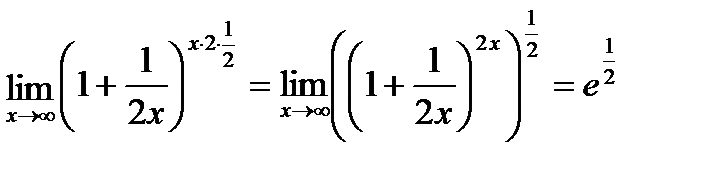
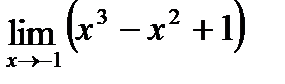 б)
б) 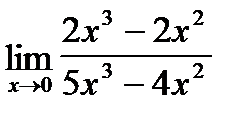 в)
в) 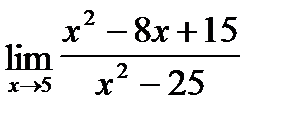 г)
г) 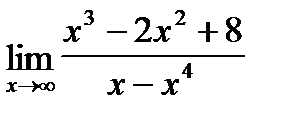
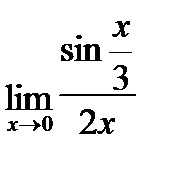 б)
б) 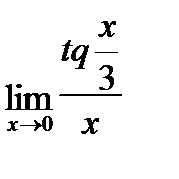 в)
в) 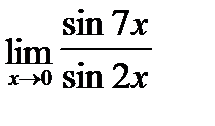
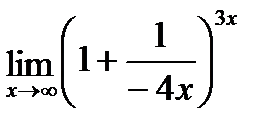 б)
б) 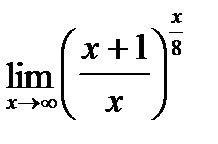
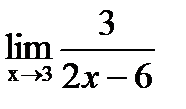
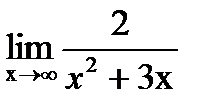
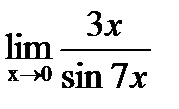
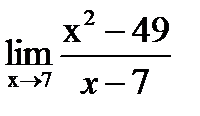
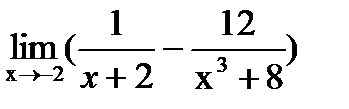
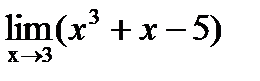
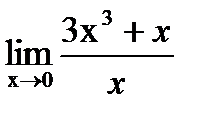
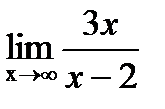
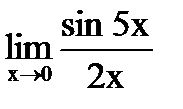

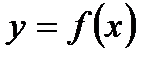 - непрерывная функция, определённая на интервале (а;b),
- непрерывная функция, определённая на интервале (а;b), 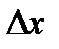 - приращение аргумента;
- приращение аргумента;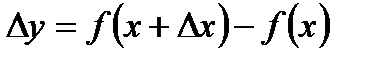 - приращение функции в точке х.
- приращение функции в точке х.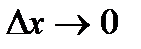 .
.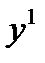 или
или 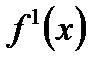 .
.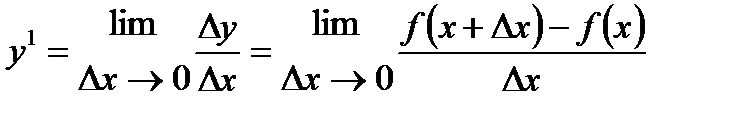

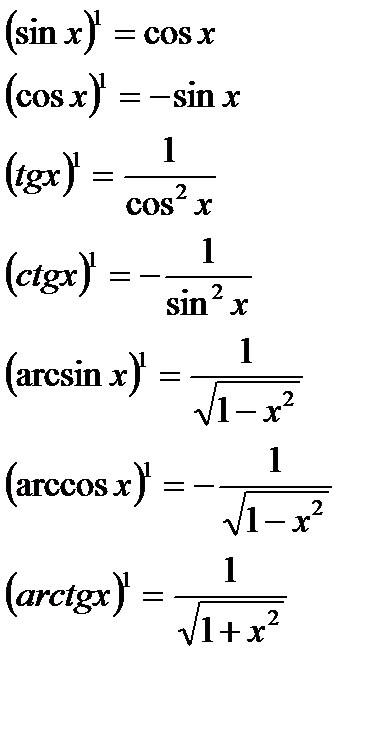

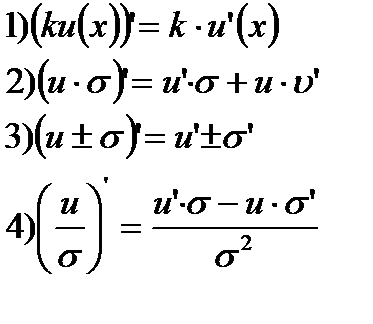
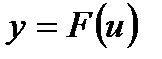 , где
, где 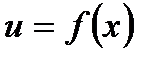 , то есть если у зависит от х через промежуточный аргумент u, то
, то есть если у зависит от х через промежуточный аргумент u, то 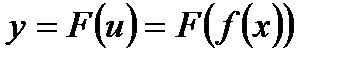 называется функцией от функции или сложной функцией.
называется функцией от функции или сложной функцией.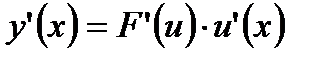
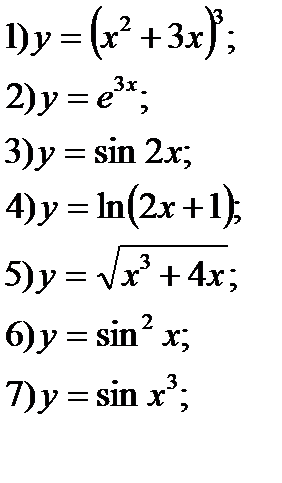
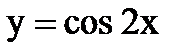 ;
;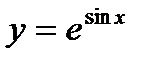 .
.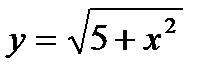
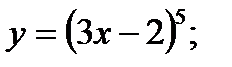
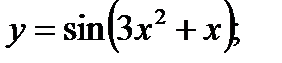
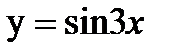
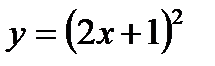
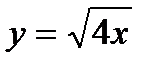 ;
;