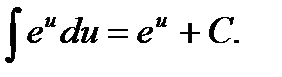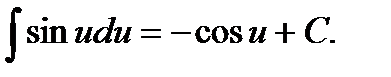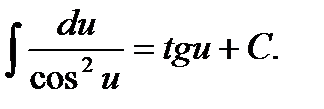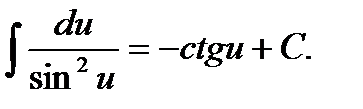Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Производная функции нескольких переменных
Для нахождения производной функции нескольких переменных используют частные производные первого, второго и т.д. порядков. При этом та переменная, по которой производная не находится, считается константой. Для нахождения частных производных справедливы обычные правила и формулы дифференцирования. Определение 4. Частной производной от функции z=f(x,y) по независимой переменной х называется конечный предел
Обозначается:
Определение 5. Частной производной от функции z=f(x,y) по независимой переменной y называется конечный предел
Обозначается:
Определение 6. Частными производными второго порядка от функции z=f(x,y) называются частные производные от ее частных производных
Входной контроль 1.Определение функции двух переменных 2.Определение функции трех переменных 3.Определение функции нескольких переменных 4.Определенеие частной производной функции двух переменных по переменной х 5.Определенеие частной производной функции двух переменных по переменной у 6. Определение частных производных второго порядка Ход работы 1. Найти частные производные первого порядка 1) z= 5sinx-2cosy 2) z=6x2y3 3) z=x2-3xy-4y2 4) z=1-x+2y 5) z=siny 2. Найти частные производные второго порядка 1) z=x4y2 2) z=x3-3xy-4y5 3) z=siny-cosx
Выходной контроль 1 вариант 1.Найти частные производные первого порядка (каждое задание 1 балл) 1) z= 3 2) z=x7y5 3) z=2ctgy-lnx
2.Найти частные производные второго порядка (каждое задание 2 балла) 1) z=7x3y6 2) z=2x+5x 3y-y4 2 вариант 1.Найти частные производные первого порядка (каждое задание 1 балл) 1) z= 3ctgx-lny 2) z=x3y4 3) z=tgy-3
2.Найти частные производные второго порядка (каждое задание 2 балла) 1) z=3x5y2 2) z=x9-x y4+3y2
Критерии оценки:
Практическое занятие № 13 Тема: Интегрирование простейших функций Цель: Научиться интегрировать простейшие функции Теоретические основы Функция F(x),
Совокупность (множество) всех первообразных от данной функции называется неопределенным интегралом от этой функции. Операция нахождения совокупности первообразных называется неопределенным интегрированием. Интегрирование есть действие, обратное дифференцированию. Неопределенный интеграл от функции f (x) обозначают символом ∫ f (x) dx здесь х - переменная интегрирования, f (x) - подынтегральная функция, dx -дифференциал переменной интегрирования, f (x) dx - подынтегральное выражение. По определению неопределенного интеграла имеем ∫f(x)dx = F(x)+C, где F(x) - любая первообразная от функции f(x) - любая первообразная от Свойства неопределенного интеграла. I. II. III. IV. V. VI. Таблица интегрирования 1. 2. 3. 4. 5. 6. 7. 8.
|
|||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2020-11-11; просмотров: 168; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.142.153.224 (0.012 с.) |
||||||||||||||||||||||||||||
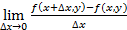 ,
,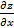 ,
, 
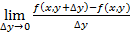 ,
,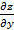 ,
, 
 =
= 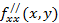
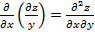 =
= 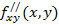
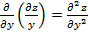 =
= 
 cosx
cosx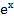 -tgy
-tgy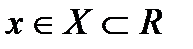 , называется первообразной для функции f(x) на множестве Х, если она дифференцируема для любого
, называется первообразной для функции f(x) на множестве Х, если она дифференцируема для любого  и F’(x)=f(x) или dF(x)=f(x)dx.
и F’(x)=f(x) или dF(x)=f(x)dx.
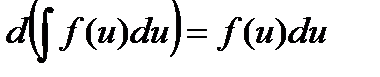
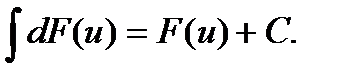

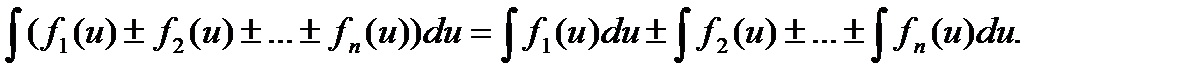
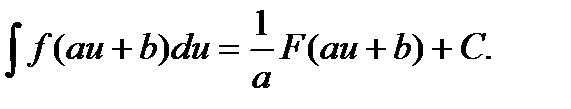
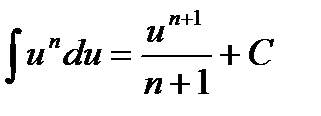 (n≠-1).
(n≠-1).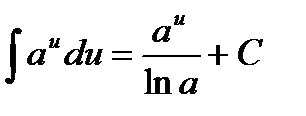 (a >0, a≠1).
(a >0, a≠1).