
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определение характеристик плоской волны, возбуждаемой поверхностным магнитным током
Исследуем электромагнитное поле волны, возбуждённой листом магнитного тока (см.п.1.5). Примем для простоты, что вектор магнитного тока направлен вдоль оси X, амплитуда его во всех точках плоскости XOY постоянна, а фаза меняется по линейному закону в направлении, совпадающем с направлением вектора тока, то есть в выражении для тока (5.1) нужно принять
Электромагнитное поле, созданное током (1.6.1), в соответствии с методикой, изложенной в п.1.5 (см.выражения 1.5.7), будет иметь следующие составляющие:

где Из формулы (1.6.3) следует, что в зависимости от величины отношения Рассмотрим отдельно случаи 1.6.1 Примем, что В этом случае Согласно (1.6.2) электромагнитное поле будет иметь следующие компоненты:
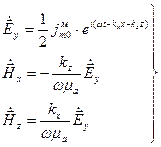
Каждая из составляющих в (1.6.4) имеет характер бегущей волны. Направление распространения волны указывается волновым вектором
Задание 1.6.1 Определить углы
Задание 1.6.2 Доказать, что уравнения (1.6.4) описывают плоскую волну. Для этого, в соответствии с материалом, изложенным в параграфе 1.2, записать уравнение волновой поверхности и проанализировать его.
Задание 1.6.3 Доказать, что плоская волна, описываемая соотношениями (1.6.4), является однородной. Для этого, в соответствии с параграфом 1.2, записать уравнение поверхности равных амплитуд и проанализировать его. Скорость движения фронта волны вдоль направления распространения - фазовая скорость - в случае
Задание 1.6.4 Определить зависимость фазовой скорости (1.6.5) от направления распространения плоской однородной волны при изменении
Задание 1.6.5 Для плоской волны, описываемой соотношениями (1.6.4), определить взаимную ориентацию векторов
Определим отношение комплексных амплитуд поперечных относительно направления распространения волны составляющих электрического и магнитного полей. В рассматриваемом случае поперечные составляющие электрического и магнитного полей имеют следующий вид:
Задание 1.6.6 Определить отношение поперечных составляющих электрического и магнитного полей плоской однородной волны, описываемой выражениями (1.6.4). Построить график
Задание 1.6.7 Определить направление переноса энергии плоской волны в пространстве, воспользовавшись выражением для вектора Пойнтинга:
где знак * над вектором Определим, как поляризовано магнитное поле плоской однородной волны, имеющей составляющие магнитного поля
В выражении (1.6.9) принято, что начальные фазы
Модуль вектора
Определим, как меняются величина и направление вектора
откуда можно сделать вывод, что положение вектора
1.6.2 Рассмотрим случай, когда
является чисто мнимой величиной. О выборе знака перед мнимой единицей было сказано ранее (см. формулу (1.3.15) и пояснения к ней). Тогда волновой вектор
Подставляя выражение (1.6.14) в соотношения (1.6.4), определим компоненты электрического и магнитного поля при

Наличие в соотношениях (1.6.15) множителя бегущей волны Волна, описываемая соотношениями (1.6.15), является плоской неоднородной волной и относится к классу поверхностных, медленных волн (см. параграф 1.1). Чтобы убедиться в этом, необходимо выполнить задания 1.6.8 и 1.6.9, учитывая общие соображения, изложенные в параграфе 1.2.
Задание 1.6.8 Получить уравнение волновой поверхности для волны, описываемой соотношениями (1.6.15), и показать, что оно является уравнением плоскости, перпендикулярной направлению распространения волны.
Задание 1.6.9 Получить из соотношений (1.6.15) уравнение поверхности равных амплитуд и показать, что оно является уравнением плоскости. Определить взаимное расположение плоскости равных фаз и плоскости равных амплитуд. Фазовая скорость волны, определяемая как скорость движения волновой поверхности вдоль направления распространения волны (в данном случае, вдоль оси X), равна:
Задание 1.6.10 Определить зависимость фазовой скорости плоской неоднородной волны от
Задание 1.6.11 Для плоской волны, описываемой соотношениями (1.6.15), определить взаимную ориентацию векторов
Задание 1.6.12 Воспользовавшись результатами, полученными при выполнении задания 1.6.11, определить поперечные составляющие векторов электрического и магнитного полей и получить выражение для отношения поперечных составляющих Выясним, переносит ли плоская неоднородная волна энергию и в каком направлении. Определим для этого вектор Пойнтинга. Подставим в выражение (1.6.8) составляющие полей
Задание 1.6.13 Получить выражения для действительной и мнимой частей вектора Пойнтинга (1.6.18). Показать, что действительная часть
Задание 1.6.14 Используя полученное из задания 1.6.13 выражение для вектора Пойнтинга, показать, что среднее значение за период колебаний мнимой части равно нулю. Сделать вывод о том, возможен ли перенос энергии этой составляющей. Построить график зависимости Определим поляризацию магнитного поля плоской неоднородной волны. Вектор напряжённости магнитного поля согласно (1.6.15) имеет две составляющие, сдвинутые по фазе во времени друг относительно друга на
где Выделим действительную часть комплексного вектора
Модуль вектора
Определим, как меняются величина и направление вектора
Из анализа выражений (1.6.21) и (1.6.22) следует, что величина вектора
Задание 1.6.15 Показать, что при фиксированном значении координаты X, например, X=0, конец вектора
|
|||||||||||||
|
Последнее изменение этой страницы: 2019-05-01; просмотров: 126; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.222.67.251 (0.046 с.) |
 . Тогда комплексная амплитуда поверхностного магнитного тока запишется в следующем виде:
. Тогда комплексная амплитуда поверхностного магнитного тока запишется в следующем виде: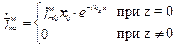 (1.6.1)
(1.6.1)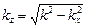 . (1.6.3)
. (1.6.3)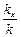 коэффициент
коэффициент  может либо иметь действительное значение (при
может либо иметь действительное значение (при  ), либо быть мнимой величиной (при
), либо быть мнимой величиной (при 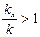 ). В зависимости от этого характер возбуждаемой волны и её свойства будут различными.
). В зависимости от этого характер возбуждаемой волны и её свойства будут различными. и
и  и может принимать значения в интервале
и может принимать значения в интервале 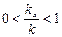 .
. - действительная положительная величина (см. формулу (1.3.14) и пояснения к ней).
- действительная положительная величина (см. формулу (1.3.14) и пояснения к ней).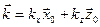 (
( ) и образует с осями прямоугольной системы координат углы
) и образует с осями прямоугольной системы координат углы  ,
,  и
и  .
. ,
,  при изменении
при изменении  .
. (1.6.5)
(1.6.5)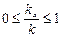 . Построить график зависимости
. Построить график зависимости  . Сделать вывод о соотношении величин фазовой скорости и скорости света в среде с заданными параметрами
. Сделать вывод о соотношении величин фазовой скорости и скорости света в среде с заданными параметрами 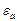 ,
,  .
.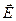 и
и  в пространстве, а также ориентацию их относительно направления распространения волны. Для этого необходимо вычислить скалярные произведения:
в пространстве, а также ориентацию их относительно направления распространения волны. Для этого необходимо вычислить скалярные произведения: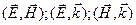 (1.6.6)
(1.6.6) (1.6.7)
(1.6.7) при
при  от направления движения плоской волны.
от направления движения плоской волны. , (1.6.8)
, (1.6.8) означает комплексное сопряжение. В выражении (1.6.8) поля
означает комплексное сопряжение. В выражении (1.6.8) поля 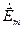 и
и  при изменении
при изменении  . Сделать выводы.
. Сделать выводы. и
и  . Из соотношений (1.6.4) следует, что составляющие
. Из соотношений (1.6.4) следует, что составляющие  и
и  вектора
вектора 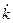 - действительные величины. Суммарный вектор напряжённости магнитного поля, полученный в результате сложения синфазных векторов
- действительные величины. Суммарный вектор напряжённости магнитного поля, полученный в результате сложения синфазных векторов  , будет иметь следующий вид:
, будет иметь следующий вид: (1.6.9)
(1.6.9) и
и 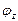 составляющих вектора
составляющих вектора  равны нулю. Действительная часть этого комплексного вектора
равны нулю. Действительная часть этого комплексного вектора (1.6.10)
(1.6.10) , описываемого выражением (1.6.10), равен:
, описываемого выражением (1.6.10), равен: (1.6.11)
(1.6.11) угол, образованный вектором
угол, образованный вектором  с осью X. Тогда из формулы (1.6.10) следует, что
с осью X. Тогда из формулы (1.6.10) следует, что , (1.6.12)
, (1.6.12) с течением времени остаётся ориентированным параллельно прямой линии, составляющей с осью X угол
с течением времени остаётся ориентированным параллельно прямой линии, составляющей с осью X угол  (рис.1.5). Таким образом, мы приходим к выводу, что в рассматриваемом случае волна линейно поляризована.
(рис.1.5). Таким образом, мы приходим к выводу, что в рассматриваемом случае волна линейно поляризована.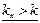 (при
(при 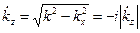 (1.6.13)
(1.6.13)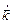 становится комплексным и может быть представлен в виде действительной и мнимой частей:
становится комплексным и может быть представлен в виде действительной и мнимой частей: (1.6.14)
(1.6.14) :
: 1.6.15)
1.6.15)
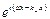 указывает на то, что волна, имеющая составляющие (1.6.15), распространяется вдоль оси X, то есть вдоль листа магнитного тока, что совпадает с направлением вектора
указывает на то, что волна, имеющая составляющие (1.6.15), распространяется вдоль оси X, то есть вдоль листа магнитного тока, что совпадает с направлением вектора  .
. (1.6.16)
(1.6.16) при изменении
при изменении  . Сделать вывод о соотношении величин фазовой скорости волны и скорости света в среде с заданными параметрами
. Сделать вывод о соотношении величин фазовой скорости волны и скорости света в среде с заданными параметрами 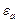 ,
, 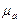 .
. и
и  в пространстве, а также ориентацию их относительно направления распространения волны. Для этого вычислить следующие скалярные произведения:
в пространстве, а также ориентацию их относительно направления распространения волны. Для этого вычислить следующие скалярные произведения: ; (1.6.17)
; (1.6.17)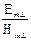 . Построить зависимость
. Построить зависимость  .
. и
и  из (1.6.15) и вычислим векторное произведение. Нетрудно убедиться, что в рассматриваемом случае вектор Пойнтинга является комплексной величиной:
из (1.6.15) и вычислим векторное произведение. Нетрудно убедиться, что в рассматриваемом случае вектор Пойнтинга является комплексной величиной: (1.6.18)
(1.6.18) равна среднему за период колебаний значению вектора Пойнтинга, характеризует перенос энергии волны вдоль плоскости XOY и совпадает с направлением распространения волны. Построить график зависимости
равна среднему за период колебаний значению вектора Пойнтинга, характеризует перенос энергии волны вдоль плоскости XOY и совпадает с направлением распространения волны. Построить график зависимости 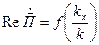 при изменении
при изменении  в диапазоне
в диапазоне 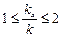 .
.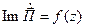 . Определить зависимость
. Определить зависимость  от
от  .
. . Представим вектор
. Представим вектор 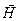 в следующем виде:
в следующем виде: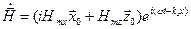 , (1.6.19)
, (1.6.19)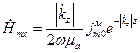 ;
;  . Начальные фазы
. Начальные фазы  и
и 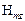 принять равными нулю.
принять равными нулю. :
: (1.6.20)
(1.6.20) в (1.6.20) равен
в (1.6.20) равен (1.6.21)
(1.6.21)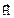 в каждой точке пространства за период колебаний. Обозначим через
в каждой точке пространства за период колебаний. Обозначим через  угол между вектором
угол между вектором  и осью Z. Тогда из выражения (1.6.20) следует, что
и осью Z. Тогда из выражения (1.6.20) следует, что (1.6.22)
(1.6.22) и направление его меняются с течением времени. При постоянном значении координаты X вектор
и направление его меняются с течением времени. При постоянном значении координаты X вектор  вращается с угловой скоростью
вращается с угловой скоростью  .
. в соответствии с выражением (1.6.21) за период колебаний описывает эллипс. Определить оси эллипса. Построить поляризационный эллипс. Сделать вывод о том, как в рассматриваемом случае поляризовано поле плоской неоднородной волны.
в соответствии с выражением (1.6.21) за период колебаний описывает эллипс. Определить оси эллипса. Построить поляризационный эллипс. Сделать вывод о том, как в рассматриваемом случае поляризовано поле плоской неоднородной волны.


