
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Нестационарный пуассоновский поток.
Это ординарный поток без последействия, для которого в любой момент времени существует конечный параметр потока λ(t). Пусть Pi(t0,τ) – вероятность поступления i -требований за интервал [ t0,t0+τ ], которая определяется формулой:
Этот параметр имеет смысл среднего числа требований на промежутке [t0,t0+τ]. Средняя интенсивность определяется как: Выбором закона изменения λ(t) можно описать реальные потоки заявок на АТС (например, отразить наличие ЧНН). Стационарный поток без последействия.
Суммирование в этой формуле производится по всем j, удовлетворяющим соотношению: Это означает, что любой неординарный пуассоновский поток можно представить как k независимых неординарных пуассоновских потоков с постоянной характеристикой неординарности l и соответствующими параметром al и интенсивностью lal. Параметр неординарного потока определяется как: а интенсивность такого потока: В качестве одного из примеров применения неординарного потока можно привести пуассоновский поток с неординарными заявками, т.е. использующим для своего обслуживания l серверов. В сотовой системе связи в том случае, когда происходит звонок с мобильного телефона на телефоны не расположенные в зоне обслуживания одной базовой станции или на телефоны городской сети, требование обслуживается одним сервером – голосовым каналом, а при осуществлении звонка на мобильный телефон, обслуживаемый одной и той же базовой станцией требуется сразу два сервера – голосовых канала. Следовательно, поток вызовов от мобильных телефонов может рассматриваться как неординарный с характеристикой неординарности равной двум. Примитивный поток.
Поток с повторными вызовами. Он состоит из потока первичных запросов – пуассоновский поток и повторных запросов. Параметр общего потока равен сумме параметров первичных и повторных заявок и может быть описан как примитивный с параметром: Здесь обозначено: i - число обслуживаемых источников, j - число источников, повторяющих запрос, α – интенсивность первичного источника, β – интенсивность источника повторного запроса. Если α ≈ ß, то потоки неразличимы. Во многих городских АТС ß >> α и можно произвести сепарацию потоков заявок по среднему времени обслуживания. Поток с ограниченным последействием. Это ординарный поток, промежутки между требованиями в котором, образуют последовательность взаимно-независимых случайных величин: Эта последовательность задается семейством функций распределения для τk. Стационарный поток с запаздыванием – поток Пальма задают условной вероятностью φ0(t) отсутствия требований в промежутке длиной t, если в начале этого промежутка было требование.
где λ – интенсивность потока Пальма, которая равна обратной величине к среднему промежутку времени между требованиями. При экспоненциальной функции вероятности отсутствия требований: Поток Эрланга Частный случай и получается “просеиванием” потока Пальма. Если отбрасывать каждую вторую заявку – то получается поток Эрланга второго порядка, если каждую третью – третьего порядка и т.д. Простейший пуассоновский поток можно рассматривать как поток Эрланга первого порядка. Обозначим pn(t) плотность вероятности промежутка между заявками. Можно получить что: Закон распределения для потока Эрланга n-го порядка:
Нормируем масштаб времени так, чтобы параметр потока не зависел от n. Τн (n)=τ(n)/n; интенсивность Λn
Нормированный поток Эрланга n – го порядка:
Обобщенный поток Эрланга n –го порядка. Если τ(n) есть сумма случайных величин, каждая из которых распределена по показательному закону с параметром λi
Поток освобождения серверов
Рис. 2, на котором показаны результаты экспериментального измерения времени занятия абонентской линии на АТС подтверждает практическую приемлемость такой аппроксимации.
Рис. 2. Гистограммы измерений длительности занятий при x = 60,3 с, s = 84,4 и разговоров при x = 81,2 с, s = 90,1 Если освободившийся сервер сразу же занимается новым обслуживанием, то отношение
В более общем случае, когда занято k серверов, вероятность освобождения i серверов за время t при показательном законе распределения времени обслуживания получим
Вероятность того, что не освободится ни один сервер: Параметр потока освобождений при занятии k серверов можно найти как предел
Поток освобождений ординарный и его параметр пропорционален числу занятых серверов. Коэффициент пропорциональности – величина обратная среднему времени обслуживания.
СРС 2 по дисциплине “Теория распределение информации»
|
||||||
|
Последнее изменение этой страницы: 2016-04-06; просмотров: 703; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.14.83.223 (0.011 с.) |
 , где
, где  .
. .
. Это неординарный (групповой) пуассоновский поток. События – моменты вызовов, представляют собой простейший пуассоновский поток с параметром λ. В каждый момент времени ti с вероятностью pl поступает группа из l (l = 1,2,… r) одинаковых заявок. Величина l – характеристика неординарности. Обозначим параметр al = λpl. Вероятность поступления k требований в промежутке времени длиной t:
Это неординарный (групповой) пуассоновский поток. События – моменты вызовов, представляют собой простейший пуассоновский поток с параметром λ. В каждый момент времени ti с вероятностью pl поступает группа из l (l = 1,2,… r) одинаковых заявок. Величина l – характеристика неординарности. Обозначим параметр al = λpl. Вероятность поступления k требований в промежутке времени длиной t: .
. .
. ,
, .
. Это ординарный поток, параметр которого прямо пропорционален числу свободных источников Ni =(N-i). Здесь N – общее число источников требований, i - число обслуживаемых в данный момент источников. Для примитивного потока параметр потока определяется как λi=αNi=α(N-i) с некоторым коэффициентом α. Среднее значение параметра примитивного потока:
Это ординарный поток, параметр которого прямо пропорционален числу свободных источников Ni =(N-i). Здесь N – общее число источников требований, i - число обслуживаемых в данный момент источников. Для примитивного потока параметр потока определяется как λi=αNi=α(N-i) с некоторым коэффициентом α. Среднее значение параметра примитивного потока:  , где fi - вероятность того, что обслуживается i источников. Средняя интенсивность потока заявок от одного источника:
, где fi - вероятность того, что обслуживается i источников. Средняя интенсивность потока заявок от одного источника: 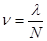 .
.
 .
. ,
, получаем простейший поток.
получаем простейший поток.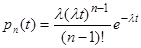 .
. ,
, .
.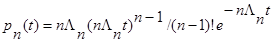
 ,
, ,
, ,
,  .
.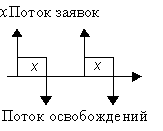 Пусть xk –длительность обслуживания k –ой заявки. При детерминированном характере обслуживания задается набор этих значений. При x = xk время обслуживания постоянно и поток освобождения совпадает по характеристикам с потоком заявок. При случайном характере обслуживания задают вероятность того, что обслуживание займет время меньшее, чем x:
Пусть xk –длительность обслуживания k –ой заявки. При детерминированном характере обслуживания задается набор этих значений. При x = xk время обслуживания постоянно и поток освобождения совпадает по характеристикам с потоком заявок. При случайном характере обслуживания задают вероятность того, что обслуживание займет время меньшее, чем x:  .
.
 , где V – общее число серверов, а
, где V – общее число серверов, а  – среднее время обслуживания. Вероятность того, что за промежуток времени t произойдет i освобождений, будет равна:
– среднее время обслуживания. Вероятность того, что за промежуток времени t произойдет i освобождений, будет равна: .
. .
. .
. .
.


