Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Наименование темы: Системы с неполнодоступным включением серверов ⇐ ПредыдущаяСтр 8 из 8
Системы с несколькими серверами могут по-разному распределять их ресурс для обслуживания поступающих заявок. Если любой свободный сервер может обслуживать любую поступающую заявку, то говорят о полнодоступном включении серверов. Если за определенными серверами закрепляются заявки, поступающие только с определенных входных линий, то говорят о неполнодоступном включении серверов (НВ).
Диаграмма интенсивностей переходов для СМО с m серверами, явными потерями и неполнодоступным включением изображена на рисунке 1:
Рис. 1. Диаграмма интенсивностей переходов для СМО с m серверами, явными потерями и неполнодоступным включением. В общем случае в неполнодоступной схеме выделяют нагрузочные группы - полнодоступные коммутационные системы, обеспечивающие подключение любого из n -входов к D -выходам, и объединительную схему, представляющую собой набор сумматоров в аналоговой схемотехнике или набор логических «или» в цифровой. В старых АТС объединительная схема реализуется в виде простых «монтажных или» в промежуточном щите переключений (ПЩ). Если считать, что имеется g -нагрузочных групп с D выходами каждая (см. рис. 2), то объединительная схема должна распределять gD выходов нагрузочных групп по m серверам (выходным линиям) фиксированным образом, т.е. часть выходов нагрузочных групп должна объединяться и подключаться к одному и тому же серверу (выходной линии).
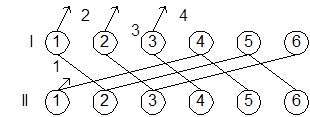
Рис. 2 Система с неполнодоступным включением.
Параметр D называют доступностью нагрузочной группы. В симметричных неполнодоступных (н.д.) схемах значения n и D одинаковы для всех групп, а в асимметричных эти значения могут различаться. Асимметричные схемы практически не поддаются расчету. Задача построения эффективной схемы НВ сводится к определению объединительной схемы, т.е. способа подключения определенным образом m выходных линий к полю из gD выходов нагрузочных групп. Необходимым условием реализации НВ является неравенство: Если m = D – это одно полнодоступное включение
Если m = gD – это g полнодоступных включений. Важной характеристикой НВ является коэффициент уплотнения: Его значение определяет сколько в среднем выходов различных нагрузочных групп подключено к одному серверу (линии). При γ < 2 слабая связность и схема имеет низкую пропускную способность На практике наиболее частоприменяют 2 < γ < 6. Большие значения γ (γ > 6) не увеличивают пропускную способность значительно, тогда как сложность сильно возрастает. По структуре объединительной схемы различают равномерный и ступенчатый способы объединения. При ступенчатом способе с ростом номера сервера растет число обслуживаемых линий, при равномерном обслуживаемые линии распределяются между серверами равномерно по числу γ на каждый или по γ+1 для некоторых. Различные примеры схем НВ показаны на рис. 3. Каждой схеме НВ можно поставить в соответствие матрицу связности
Элементы главной диагонали матрицы указывают значение доступности. Каждый элемент на пересечении i -строки и j - столбца указывает на число связей между i -ой и j -ой группами.
Матрица связности определяет оптимальную схему НВ, если
Первое условие называют условием качества перехвата, а второе условием качества перекоса. Практически приемлемые условия качества перехвата и перекоса можно легко получить, используя специфическую структуру равномерной схемы, называемой «цилиндр». На рис. 3. это схемы г) и е). Для схем типа цилиндр матрица связности циклична и m = g. Величина γ = r, которую называют числом шагов цилиндра. Схема 3. е) представляет собой пять двухшаговых цилиндров, а схема 3.г) – два одношаговых, два двухшаговых и один четырехшаговый. Для цилиндров рассчитывается только одна строка, поскольку все остальные получаются циклическим сдвигом. Анализ показывает, что среди эквивалентных по матрицам связности цилиндров можно выбрать несколько типовых схем, для которых рассчитываются все параметры. Такие схемы сведены в таблицы. Используя эти таблицы, проводят синтез объединительных схем для НВ. Более лучших результатов можно добиться использованием специальных компьютерных программ.
Теперь вернемся к аналитическому описанию СМО и определению функции φ. Если доступность НВ равна D. То следует положить
Рис. 3 Виды схем неполнодоступных включений. Для так называемой идеально симметричной схемы включения (ИСС), при которой каждой нагрузочной группе доступна своя, отличная от других комбинация D серверов, можно определить функцию φ достаточно просто. Поскольку число различных комбинаций из D серверов при общем их числе m определяется числом сочетаний Вероятность занятия фиксированных i серверов будет определяться
Например, для схемы на рис. 4 D=2,m=4,
Рис.4 Идеально симметричная НВ.
Для других отличных от ИСС схем НВ задание функции φ более сложно. Однако расчет пропускной способности произвольной схемы НВ ведут, опираясь на формулы для ИСС, если γ >2. Для приближенных расчетов выведен целый ряд формул, которые сыграли большую роль при проектировании узлов коммутации, когда применение компьютеров было сильно ограниченным. И сейчас они играют большую роль для эскизных расчетов.
|
||||||
|
Последнее изменение этой страницы: 2016-04-06; просмотров: 398; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.223.196.211 (0.01 с.) |
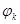 - функцию состояния k, значение которой равно вероятности обслуживания заявки, поступившей в СМО в этом состоянии. Стационарное распределение вероятностей в этом случае будет зависеть как от параметра входного потока, так и от значения
- функцию состояния k, значение которой равно вероятности обслуживания заявки, поступившей в СМО в этом состоянии. Стационарное распределение вероятностей в этом случае будет зависеть как от параметра входного потока, так и от значения 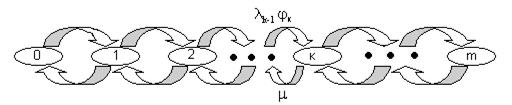

 .
.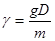 .
.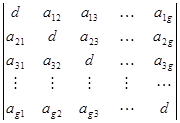
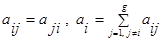 .
.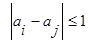 .
.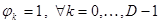 .
.
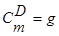 .
.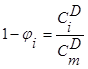 .
.