
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Понятие эконометрики. Осн-е задачи эконометрикиСтр 1 из 5Следующая ⇒
Понятие эконометрики. Осн-е задачи эконометрики Эконометрика-наука, в кот. на основе реаль-х статист-их данных, строятся, анализ-ся и совершен-тся матем-ие модели реаль-х эконом-х явл-й и процессов. Основные задачи эконометрики: · Построение эконометр-х моделей- этап спецификации · Оценка парам-ров построения модели- этап параметризации · Проверка кач-ва найд-ых парам-ров модели и самой модели в целом - этап верификации · Исполь-ие постр-ных моделей для объясн-ия поведения исслед-ых эк-ких пок-лей для прогноз-ния, а также для проведения осмысл-ой эконом-ой политики Метод наимен квадратов (МНК) Согласно МНК эмпирические коэффициенты регрессии b0 и b1 определяются из того факта, что сумма квадратов расстояний эмпирических значений зависимой переменной
Необходимым условием существования минимума функции2-х переменных является равенство нулю ее частных производных по неизвестны параметрам b0 и b1
Для практических расчетов последние формулы применять не рекомендуется, т.к. в них происходит округление данных. Лучше использовать след формулы
Коэффициент корреляции.
Для практических расчётов коэф-в корреляц. изменяется от -1 до 1. Если коэф-т корреляц. = 0, то значит, что X и Y некоррелир., если rxy =1, то полная прямая корреляц., если rxy = - 1 – полная обратная корреляц., если 0 <rxy<1, то коррел. – положит. Это знач., что с возрастанием 1-й перемен. возр. и 2-я, если -1<rxy<0, то 1-я возр, а 2-я убывает.
6.Предпосылки метода наименьших квадратов (МНК). Доказано, что для получения по МНК наилучших оценок необходимо, чтобы выполнялись предпосылки (условие Гаусса-Маркова) относит. случайных отклонений. · Мат. ожид. случ. отклонения для всех наблюдений =0. Отклонение в среднем не оказ. влияния на зав. переменную · Дисперсии случ-х отклон-й явл. пост. вел-й для любых наблюдений · Случ отклонения Еi и Еj явл. незав. друг от друга для i ≠ j, т.е. некоррелиров. · Выполнимость дан. предпосылки указ. на отсутствие автокорреляции · Случ. отклон-е должно быть независимым от экзогенных переменных (M(ЕiXi)) = 0 · Модель должна быть линейной относительно параметров Теорема Гаусса-Маркова
Если выполн. предпос. 1-5, то оценки, полученные по МНК явл. · несмещёнными. (Это знач., что ср. значение М(b0) = β0, М(b1) =β1)) · оценки явл. состоятельными. Это знач. что их дисперсии при ↑ числа наблюд-й → к 0. · оценки явл. эффект. Это знач., что они имеют наименьшую дисперсию по сравнению с люб. др. оценками
7. Анализ точности определения оценок коэффициентов регрессии Оценки коэффициентов регрессии b0 и b1 является тем надежнее, чем меньше их дисперсии. D(b0) и D(b1), то есть чем меньше их разброс вокруг β0 и β1. Надежность оценок тесно связана с дисперсией случайных отклонений, фактически Выведем формулы связи дисперсий оценок коэффициентов с дисперсией случайных отклонений. Для этого представим формулу для определения b0 и b1 в виде линейных функций относительно значений переменной У:
Обозначим
Так как предполагается, что дисперсия У постоянна и не зависит от Х, ci и di можно рассмотреть как некоторые постоянные, следовательно:
Из функции 1 и 2 видно, что: 1. Дисперсии оценок прямо пропорциональны дисперсии случайного отклонения, следовательно, чем больше фактов случайности, тем менее точными будут оценки. 2. Чем больше число наблюдений n, тем более точными будут оценки. 3. Чем больше дисперсия объясняющей переменной, тем меньше дисперсия оценок коэффициентов. Но так как случайные отклонения εi по выборке определены быть не могут, то при анализе надежности оценок они заменяются оценками:
В этом случае выборочные исправления дисперсии будут иметь вид:
Показательная модель.
В общем случае Y =β0 Данная функция к исходной вследствие тождества: Ряд экономических показателей моделируется через функции, являющиеся композицией перечисленных функции, что позволяет свести их к линейным. Например, производственная функция Кобба-Дугласса с учетом научно-технического прогресса: Y = ln Y = ln A+αln K+βln L + yt, которое сводится к линейному заменами ln Y =y, ln A= a, ln K = k, ln L= l. 32. Метод ведущего критерия. В этом методе все критерии кроме самого важного переводятся в разряд ограничений. Умножив все критерии минимизированной ф-ции на (-1) и обозначив через β=( max F(x)=
27.Преобр-е случ.отклон-ий. Важн.значение имеет выпол-сть опред.предпосылок МНК для случ.отклонений.Они требуют,чтоб отклонения εi явл-сь нормально распред-ми случайн. величинами с нулевым мат. ожид-ем и постоян. дисперсией σ2 и не коррелировали др. с другом (εi~N(0;σ2),cov(εi,ε j )=0 при i≠j). При невыполнтмости указан. предпосылок оценки, получен. по МНК, не будут обладать св-ми BLUE-оценок, и проводимые для них тесты окаж-ся ненадежн. Если совокупн. Логарифмир-ние не треб-ся, с аддитив-м случайн. членом выполнимость предпосылок МНК имеет место, а следов-но, нет проблем с оцениваем. Для описания возможн.проблем со случ-м отклон-ем. воспользуемся моделью Y=A*XB, дополнив ее случ-м членом. Случайный член ε может входить в соотнош-е в различн.видах. Рассмотрим 3 возможн. случая: Y=A*XB*ee (1);Y=A*XB*e (2); Y=A*XB+e (3).Данн. модели явл-ся нелин-ми относ-но параметра β. Прологарифмировав кажд.из этих соотнош-й, соответ-но получим: lnY=a+β*lnX+ε (4); lnY=a+β*lnX+lnε (5); lnY=ln(A+Xβ+ε) (6). Здесь a=lnA. Использов-е(4)для оценки параметров в(1)не вызывает осложнений, связ-х со случ-м тклон-ем.Преобраз-е(2)в(5)приводит к преобр-ю случ. отклонений εi в lnεi. Использ-ние МНК в(5)для нахождения BLUE- оценок параметров требует, чтобы отклон-я νi=lnεi удовлетв-т предпос-ам МНК: νi~N(0, σ2). Но это возможно только в случае логарифм-ски нормальн.распред-я СВ εi c M(εi)=e(y^2)/2 и D(εi)=ey^2(ey^2-1). Логариф-кое соотнош-е(3) не привело к линеаризации соотнош-я относит-но парам-ов. Т.о. при исполь-нии преобраз-ний с целью нахожд-я оценок необходимо особ. вним-е уделять св-вам случайн.отклон-й, чтобы получен-е в результате оценки имели высок.статистич.значимость.
28. Постановка и математическая модель задачи векторной оптимизации. Многие экон.-управленческие задачи яв-ся многоцелевыми, напр., производственная программа предприятия д. обеспечить максим. возможный объем выпуска продукции, низкую ее себестоимость, высокие показатели рентабельности и др. В силу этого оптимальное решение по 1-му критерию м. оказаться не лучшим по другим критериям. Множество критериев м. представить в виде векторной целевой функции F(x)=(f1(x), f2(x),…, fK(x)). Для того, чтобы минимизировать частный критерий fK(x), достаточно максимизировать fk(x), т.к. min fk(x)=-max fk(x). Поэтому будем считать, что в дальнейшем каждая компонента векторного критерия максимизируется. Задача многоцелевой оптимизации записывается как векторная задача математического программирования:
max F(x) = (f1(x), f2(x),…, fK(x)) (1)
xj Будем рассматривать задачу 1-3 для случая, когда оптимальные решения Найти решение, при котором значения всех критериев одновременно будет наилучшим, можно в области компромисса, кот. Находится в области допустимых решений. Решения, кот. Доставляют критериям наилучшие значения одновременно, называются эффективными, компромиссными, оптимальными по Паретто. План Х1 не хуже плана Х2, если fk(Х1) Если среди последних неравенств хотя бы 1 строгое, то план Х1 наз-ся предпочтительнее плана Х2. План Х1 оптимален по Паретто, если он допустим и не существует другого плана Х2, для кот. fk(Х1)
39. Если в матрич. игре ниж. и верх. чистые цены совпад-т, т.е. α=β,то такие игры наз.играми с седловой точкой.Знач-е υ=α=β наз.чистой ценой игры,а стратегии
Понятие эконометрики. Осн-е задачи эконометрики Эконометрика-наука, в кот. на основе реаль-х статист-их данных, строятся, анализ-ся и совершен-тся матем-ие модели реаль-х эконом-х явл-й и процессов. Основные задачи эконометрики: · Построение эконометр-х моделей- этап спецификации · Оценка парам-ров построения модели- этап параметризации · Проверка кач-ва найд-ых парам-ров модели и самой модели в целом - этап верификации · Исполь-ие постр-ных моделей для объясн-ия поведения исслед-ых эк-ких пок-лей для прогноз-ния, а также для проведения осмысл-ой эконом-ой политики
|
|||||||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 343; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.147.36.213 (0.023 с.) |
 от расчетных значений
от расчетных значений  должна быть минимальной.
должна быть минимальной. →min
→min

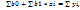

 ,
,
 Разделим все на n
Разделим все на n , →
, → 

 .
.


 является дисперсией D(У/хi) случайной переменной У.
является дисперсией D(У/хi) случайной переменной У. , так как
, так как 
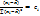 , тогда
, тогда 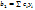
 ,
,  ;
; 
 (1)
(1) (2)
(2) , а их дисперсии заменяются несмещенной оценкой
, а их дисперсии заменяются несмещенной оценкой .
. ,
, , где
, где  – необъясненная дисперсия – доля разброса зависимой переменной, которая не объясняется регрессией.
– необъясненная дисперсия – доля разброса зависимой переменной, которая не объясняется регрессией.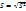 – стандартная ошибка регрессии
– стандартная ошибка регрессии и
и  – стандартные ошибки оценок коэффициентов регрессии.
– стандартные ошибки оценок коэффициентов регрессии.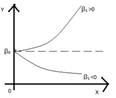 Показательная модель: Y = β0еβ1 Х. Важным ее приложением является ситуация, когда анализируется изменение переменной Y постоянным темпом прироста во времени. В этом случае переменная Х символически заменяется переменной t: Y=β0
Показательная модель: Y = β0еβ1 Х. Важным ее приложением является ситуация, когда анализируется изменение переменной Y постоянным темпом прироста во времени. В этом случае переменная Х символически заменяется переменной t: Y=β0  . Данная функция путем логарифмирования (ln eβ1t = β1t) сводится к лог –линейной модели: ln Y = ln β0 + β1t/
. Данная функция путем логарифмирования (ln eβ1t = β1t) сводится к лог –линейной модели: ln Y = ln β0 + β1t/ ,где
,где  -произвольная положительная константа,
-произвольная положительная константа,  .
. .
. . Прологарифмировать данную функцию, получим соотношение:
. Прологарифмировать данную функцию, получим соотношение: ) нижние границы соотв. критериев,тогда матем. модель задачи будет иметь вид:
) нижние границы соотв. критериев,тогда матем. модель задачи будет иметь вид: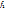 (x);
(x);  (x)≥
(x)≥  , k=
, k=  ;
;  (x)
(x) 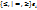 , i=
, i=  ,
, 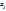 ≥0, j=
≥0, j= 
 (2)
(2) , j=
, j=  (3)
(3) , k=
, k=  полученные при решении задачи по каждому решению не совпадают.
полученные при решении задачи по каждому решению не совпадают.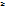 fk(Х2), k=
fk(Х2), k=  наз. оптимальными чистыми стратегиями. Пара чис.стр-гии (
наз. оптимальными чистыми стратегиями. Пара чис.стр-гии (  ) наз. седловой точкой матрич.игры. Элемент
) наз. седловой точкой матрич.игры. Элемент  наз.седловым элементом платёж.матрицы.Признаком матрич.игры с седловой точ. явл.выраж.
наз.седловым элементом платёж.матрицы.Признаком матрич.игры с седловой точ. явл.выраж.  =
=  Элемент
Элемент  и наиб-м в столбце
и наиб-м в столбце  Решением явл.тройка чисел (
Решением явл.тройка чисел (  )
)


