|
Понятие корреляции и регрессии. Виды регр-й и корр-ий. Задачи регр-ого и корр-ого анализа.В эк-ке между процессами и явл-ями сущ-ет 2 вида завис-ти: функц-ная (когда на исследуемый пок-тель действуют только рассмотр-ые факторы и никакие др. не оказыв-т существенного влияния) и статист-ая (стохастическая, вероятностная) (завис-сть между переменными, когда каждому значению одной переменной соответ-ет множ-во возможных знач-ий другой переменной). В силу неоднозначности стат-кой завис-ти между переменными X и Y интерес представляет завис-ть –как независ-ая переменная Х влияет на завис-ую переменную Y «в среднем», т. е. завис-ть в измерении мат. ожидания случайной переменной Y вычисленного в предположении, что переменная Х принимает знач-е х. Такая завис-ть – корреляционная, которую можно описать с помощью ф-ции регрессии Y по Х М(Y/Х=х)=М(Y/х)=Мх(Y)=f(x) (1) Завис-ая переменная Y - объясняемая, выходная, эндогенная, а Х -объясняющая, входная, экзогенная.
Т.е. связи между эндогенными и экзогенными переменными можно выразить соотношениями: Y=М(Y/х)+ξ Виды регрессии: 1.Простая(парная)- завис-ть между 2-мя переменными; 2.Множ-венная регрессия – регрессия между завис-ой и несколькими независ-ми переменными; 3.Линейная регрессия – описывается линейной ф-цией; 4.Нелинейная регрессия – описывается нелинейной ф-цией; 5.Положительная – когда с увеличением или уменьшением независ-ой переменной соответственно увеличивается или уменьшается завис-ая переменная; 6.Отрицательная – когда с увеличением или уменьшением независ-ой переменной соответственно уменьшается или увеличивается завис-ая переменная. Различают еще: · Непосредственную - завис-ая и независ-ая переменные непосредственно связаны между собой · Косвенную - независ-ая переменная действует на завис-ую через ряд завис-ых переменных · Множ-венную – строится, если между переменными сущ-ет какая-либо завис-ть. Задачи регрессионного анализа: 1.установление вида завис-ти между эк-ми переменными 2.определение ф-ции регрессии 3.определение неизвестных значений завис-ой переменной Если определяется значение завис-ой переменной вне интервала завис-ых переменных, то такая задача наз-сяэкстраполяцией, а если определяется знач-е внутри интервала заданных значении – интерполяцией. Корреляция тесно связана с регрессией, если в регрессионном анализе исследуется форма завис-ти, то в корреляционной – сила и степень этой завис-ти. Задачи корреляционного анализа: 1.измерение степени завис-ти 2-х или более эк-их пок-телей 2.отбор факторов, оказывающих наиболее сильное влияние на завис-ую переменную 3.обнаружение неизвестных завис-тей.
Задача сост-т в том,чтобы по конкретн.выборке найти b0 и b1такие,чтобы построен-ая линия регрессии явл-сь бы наилучш.среди др.,т.е. была бы ближаеш.к точкам наблюд-й по их сов-ти. |
||
|
Последнее изменение этой страницы: 2016-04-07; Нарушение авторского права страницы infopedia.su не принадлежат авторские права, размещенных материалов. Все права принадлежать их авторам. Обратная связь - 54.224.210.130 |
Завис-сть 2-х случ-ых величин - парная регрессия, а завис-ть нескольких переменных - множ-венная регрессия. М(Y/х1,х2,…, хm)=f(x1,x2,…,xm)
Для того, чтобы отразить тот факт, что реальные значения завис-ой переменной не всегда совпадают с ее условными мат. ожиданиями и могут быть различными при одном и том же значении независ-ой переменной фактическая завис-ть должна быть дополнена некоторым слагаемым ξ, которая является случ. величиной и указывает на стохастическую суть завис-ти.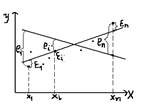
3. Парная линейная регрессия-линейн. фун-ия между условн. мат. ожиданием- М(У/хi)зависимой переменной У и одной независим. переменной Х: (1)М(У/хi)=β0 + β1хi,i=1;n,где хi-знач-я независ. переменной в i-ом наблюдении.Чтоб показать,что кажд.индивидуальн.значение уi отклон-ся от соответств-го условн.мат.ожидания в (1) надо ввести случ-ое слагаемое εi: уi=М(У/хi)+εi=β0+β1хi+εi; i=1;n.←это наз-ся теоретич-й регресс-ой линейн.моделью. β0;β1-теоретич-е коэф-ты регрессии; εi-теоретич-е случ-ое отклонение.Общий вид теоретич-й линейн. регресс-ой модели→ У= β0+β1Х+εi.Чтоб определить значения теоретич.коэф-тов регрессии надо знать ХиУ генеральн.сов-сти,что практич-и невзможно.След-но,по выборке огранич-го объёма (хi;уi),i=1;n мы строим эмпирич-е ур-ние регрессии.(2) 
= b0 + b1хi, i=1;n, где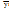 
+ei,i=1;n, ei-оценка случайн. отклон-я εi.Т.к. генеральн.сов-ть практически всегда неизв-на,то оцененные парам-ры b0 и b1,от истинных знач-ий β0иβ1.