
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Метод равных и наименьших относительных отклонений. ⇐ ПредыдущаяСтр 5 из 5
Будем решать задачу по К-критериям:
Запишем условие равенства относительных отклонений значений критериев от их экстремальных значений.
Рассмотрим 4 первых критерия. По условию задачи f1,f2 – максимизируются, f3,f4 – минимизируются. Проанализ-м знач-я относит. отклонений первых 2ух критериев. Если f2*<0 и f1*<0,то тогда Если f2*>0 и f1*>0,то тогда Поэтому в равенстве относительных отклонений этих критериев модуль абсолютных величин можно опустить, тогда получим: Введём обозначения, что
Для критериев f3,f4 получим точно такое же ур-е, т.к. направления их оптимизации совпадают. Рассмотрим критерии с противоположным направлением оптимизации. Если f1*<0 и f3*<0,то тогда Если f1*>0 и f3*>0,то тогда Поэтому при опускании знака модуля перед одним из выражений ставим «-».
Т.о. для нахождения компромиссного реш-я рассматриваемым методом необходимо оптимиз-ть критерии включённые в число неизвестных задачи и к осн. ограничениям добавить след. ограничения:
36. Во всех областях чел. деят-ти встреч. проблемы принятия управ. реш-й в усл-х неопределенности. При этом неоп-ть м.б. связана как с сознательными действиями конкурента, так и др. факторами, влияющими на эфф-ть прин. реш-я. Ситуации, в кот. эфф-ть прин. одной стороной реш-я зависит от действ. др. стор. наз. конфликтными. Теория игр – раздел мат., изуч. конфл. ситуации на основе мат. моделей, т.е. это мат. теория, разраб-я оптим. правило поведения кажд. из участников в конфл. ситуации. Конфл. сит-я наз. антагонистической, если увел-е выигрыша одной из сторон на некот. вел-ну приведет к уменьш-ю выигрыша др. ст. на такую же вел-ну и наоборот. Стратегия игрока – сов-ть правил, однозначно опред-щих послед-ть действий игрока в конкр. конфл. сит-и. Стратегия игрока наз. оптим., если она обеспеч. данн. игроку при многократном повторении игры максим. возм. средний выигрыш или миним. возм. средний проигрыш независ. от поведения конкурента. Партией наз. каждый вариант реализации игры опред.обр. выбор одной из стратегий и ее реализ-я наз. ходом. Ход наз. личным, если игрок сознательно выбир. 1 из стратегий. Ход наз. случ., если выбор осущ-ся в случ. механизме. В зав-ти от кол-ва уч-ков игры подразд. на конечные и бескон. В конце партии кажд. игрок Ai, i=
37. Матричные игры с нулевой суммой. Будем рассматривать парные конечные игры, т.е. у каждого из 2х игроков А и В конечное число стратег. В большинстве случаев мы имеем игры с нулевой суммой, т.е. игры, в которых выигрыш 1го игрока равен проигрышу другого. Парную конечную игру удобно исследовать, если она записана в виде платежной матрицы:
Здесь каждое число аij, i=1,m j=1,n является действительным числом и представляет собой сумму выигрыша, уплачиваемую игроком В игроку А, если игрок А выбирает стратег. соотв. i-той строке, а игрок В выбирает стратег. соотв. j-тому столбцу. Такую игру называют матричной игрой размерности m на n. Целью участников любой матричной игры, явл. выбор наиб. выгодной стратег., кот. доставляют А max выигрыш, а В – min проигрыш. Чистая стратегия – Аi, i=1,m игрока А (Bj, j=1,n игрока В) назыв. Возможный ход игрока А (В) выбранный им с вероятностью 1. Если игра состоит из матричных ходов, то выбор пары чистых стратег. (Ai, Bj) единственным образом определяет исход игры. Если в игре исп-ся случ. ходы, то исход игры определяется математическим ожиданием (ср.знач.). Стратег. А назыв. оптимальной, если при ее применении выигрыш игрока А не ¯, какими бы стратег. не пользовался игрок В. Оптим. стратег. для В явл. стратег., при которой проигрыш игрока В не , какими бы стратег. не пользовался игрок А.
38. Решение матричных игр в чистых стратегиях. Если игрок А имеет m, а игрок В – n стратег., то для любой пары стратег. игроков, их чистые стратег. можно представить в виде единичных векторов. Например, для пары стратег. (Ai, Bj) – ед.вектор: pi= (0…0,1,0…0) и qj= (0…0,1,0…0). При нахождении оптим.стратег. игроки исп-т принцип осторожности, при кот.игроки считаются одинаково разумны, используя этот принцип, найдем оптим.стратег. А и В.
Игрок А для каждой стратег. Аi, i=1,m, сначала найдет min знач. выигрыша: αi =min(j) aij,i=1,m Затем среди αi выберем max: α= max(i) αi. Величина α назыв. нижней чистой ценой игры (максимином): α = max(i) min(j) aij α гарантированный выигрыш, кот.может обеспечить игрок А, при любом поведении В. Стратег. Аi* обеспеч.получение нижней цены игры – максиминная стратег. Игрок В для кажд.стретег. Bj j=1,n, выберет max значение: βj= max(i) aij, j=1,n. Затем из βj выберет min знач.: β= min(j) βj Стратег. Bj* обеспеч. верхнюю чистую цену игры и назыв. минимаксом Теор. 1: В матричн.игре нижн. цена игры не превосходит верхн.чист.цены игры, т.е. α <= β Док-во: По определению αi =min(j) aij <= aij и βj= max(i) aij >= aij, значит объединим последнее в соотнош: αi =min(j) aij <= aij <= βj= max(i) aij, аслед-но αi<= aij<= βj или αi <= βj. Данное нер-во справедливо при любых комбинациях i и j, оно будет справедливо и для тех i и j, для кот. α= max(i) αi и β= min(j) βj след-но для этих i и j α <= β
|
|||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 641; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.226.96.61 (0.007 с.) |
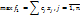
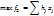
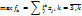
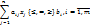
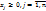
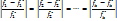


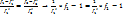
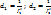
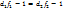
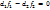

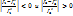
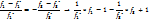

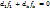 , для всех fk, которые как и f1 максимизируются
, для всех fk, которые как и f1 максимизируются , для всех fk, которые минимизируются.
, для всех fk, которые минимизируются. получ. некот. сумму ai, i=
получ. некот. сумму ai, i= 


