
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
I. Повторение изученного материала.⇐ ПредыдущаяСтр 12 из 12
1. Повторить правила сложения, вычитания и умножения чисел с разными знаками и отрицательных чисел. Привести свои примеры. 2. Решить № 1132 (а – г) устно. 3. Повторить определение модуля числа и решить № 1133. 4. Решить № 1136 устно. Привести свои примеры. II. Тренировочные упражнения. 1. Решить № 1122 с комментированием на месте. 2. Решить № 1127 (б) на доске и в тетрадях. Решение. б)
3. Решить № 1124 (устно), формулируя правила. 4. Решить № 1123 (ж; з; и) на доске и в тетрадях. Решение. ж) з) и) 5. Решить № 1131 (а) устно. 6. Решить № 1130 (г; д; е) на доске и в тетрадях. Решение. г)
д)
е)
7. Повторение ранее изученного материала. Решить № 1141 (г; д) на доске и в тетрадях. Решение. г) Пусть высота сосны равна х м, тогда высота ели 0,4 х м. х – 0,4 х = 1,2 0,6 х = 1,2 х = 1,2: 0,6 = 12: 6 х = 2. Высота сосны 2 м, высота ели 2 · 0,4 = 0,8 (м). Ответ: 2 м; 0,8 м. III. Самостоятельная работа. Вариант I. 1. Выполните умножение: а) –59 · (–11); б) –5,4 · 0,9; в) 2. Выполните действия:
3. Найдите значение выражения 4. Дополнительно: решить № 1142 (1). Вариант II. 1. Выполните умножение: а) 49 · (–14); б) –4,2 · (–0,7); в) 2. Выполните действия:
3. Найдите значение выражения 4. Дополнительно: решить № 1142 (2). Домашнее задание: № 1143 (и – м), № 1145 (г – е), № 1146. ДЕЛЕНИЕ Урок 1 Цели: ввести правила деления отрицательных чисел и деления чисел с разными знаками; научить применять эти правила при выполнении упражнений. Ход урока I. Анализ самостоятельной работы. 1. Указать ошибки, сделанные учащимися при выполнении работы. 2. Решить на доске упражнения, вызвавшие затруднения у учащихся. II. Устная работа. 1. Решить № 1164 (а; б; в; д) устно; повторить правила умножения чисел. 2. Решить № 1162 устно. III. Коллективная поисковая работа по изучению материала. 1. Деление отрицательных чисел имеет тот же смысл, что и деление положительных чисел: по данному произведению и одному из множителей находят второй множитель. Привести свои примеры. Пишут: –12: (–4) = 12: 4 = 3; –4,5: (–1,5) = 45: 15 = 3;
2. Сформулировать правило деления отрицательного числа на отрицательное число. Привести свои примеры. 3. В ходе рассуждений и поисковой работы подвести учащихся к правилу деления чисел с разными знаками:
–24: 4 = –6; 24: (–4) = –6. 4. Сформулировать правило деления чисел с разными знаками. Привести свои примеры. Важно подчеркнуть, что обычно вначале определяют и записывают знак частного, а потом уже находят модуль частного. Примеры. 3,6: (–3) = – (3,6: 3) = –1,2;
5. При делении нуля на любое число, не равное нулю, получается нуль. 0: (–17) = 0; 6. Делить на нуль нельзя! IV. Закрепление изученного материала. 1. Решить № 1149 устно. 2. Решить № 1150 (а – в) на доске и в тетрадях; № 1150 (г; д) – самостоятельно. 3. Решить № 1158 (а; б) на доске и в тетрадях, № 1158 (в; г) – с комментированием на месте. Решение. а) б) 4. Решить № 1152 (б; в) на доске и в тетрадях, № 1152 (а; д; е) –самостоятельно с проверкой. Решение. а) –4 · (–5) – (–30): 6 = 20 – (–5) = 20 + 5 = 25; б) 15: (–15) – (–24): 8 = –1 – (–3) = –1 + 3 = 2; в) –8 · (–3 + 12): 36 + 2 = –8 · 9: 36 + 2 = –72: 36 + 2= –2 + 2 = 0; д) (–8 + 32): (–6) – 7 = 24: (–6) – 7 = –4 + (–7) = –11; е) –21 + (–3 – 4 + 5): (–2) = –21 + (–2): (–2) = –21 + 1 = –20. 5. Решить № 1154 (объясняет решение учитель). 6. Повторение ранее изученного материала. Решить № 1166 (б) самостоятельно с проверкой. V. Итог урока. 1. Сформулируйте правило деления отрицательного числа на отрицательное. Привести свои примеры. 2. Сформулируйте правило деления чисел, имеющих разные знаки. Привести свои примеры. 3. Чему равно частное 0: а, где а? 0? 4. Выполните деление (устно): а) –55: 5; в) –10: (–2,5); б) 3,6: (–9); г) Домашнее задание: выучить правила п. 36; решить № 1172 (а – г), № 1174 (а; б), № 1176. Урок 2 Цели: научить учащихся применять правила деления и умножения чисел при решении примеров и задач; закрепить правила деления и умножения обыкновенных дробей и десятичных дробей; развивать логическое мышление учащихся. Ход урока I. Устная работа. 1. Повторить правила умножения и деления отрицательных чисел и чисел с разными знаками. Привести свои примеры. 2. Повторить правило деления обыкновенных дробей. Решить № 1160 (б) устно. 3. Повторить правило умножения десятичных дробей. Решить № 1164 (г; е; ж) устно. 4. Решить № 1165 устно. Решение. 9 = 3 · 3 = (–3) · (–3); 16 = 4 · 4 = (–4) · (–4); 25 = 5 · 5 = (–5) · (–5). II. Выполнение упражнений. 1. Решить № 1150 (е; ж; и) самостоятельно, № 1150 (к; л; м) – на доске и в тетрадях.
2. Решить № 1158 (и; к) на доске и в тетрадях. и) к) 3. Решить № 1151 (а; б; д; е) (объясняет учитель), № 1151 (в; г; ж) – с комментированием на месте. Решение. а) б) в) ж) 4. Решить уравнения № 1156 (а; б) на доске и в тетрадях. Решение. а) б) 5. Найти неизвестный член пропорции, решить № 1159 (а; б). Повторить определение пропорции и основное свойство пропорции. Решение. а)
б)
6. Решить № 1152 (г; ж; з) самостоятельно. Три ученика самостоятельно решают на доске, остальные в тетрадях, а затем проверяется решение. Решение. г) 2,3 · (–6 – 4): 5 = 2,3 · (–10): 5 = –23: 5 = –4,6; ж) –6 · 4 – 64: (–3,3 + 1,7) = –24 – 64: (–1,6) = –24 + 40 = 16; з) (–6 + 6,4 –10): (–8) · (–3) = –9,6: (–8) · (–3) = 1,2 · (–3) = –3,6. 7. Повторение ранее изученного материала. Решить № 1168 (а; б). III. Итог урока. 1. Повторить правила умножения и деления чисел, правила знаков. 2. Решить № 1155 (а; б) устно. Домашнее задание: повторить правила п. 35 и 36; решить № 1172 (д – з), № 1174 (в; г), № 1173 (а; б), № 1177 (а). Урок 3 Цели: повторить и закрепить изученный материал, способствовать выработке навыков и умений решения примеров и задач и применения при этом изученных правил; проверить знания учащихся в ходе самостоятельной работы. Ход урока
|
||||||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 347; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.58.137.218 (0.015 с.) |

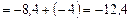 .
.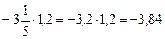 ;
; ;
; .
.
 ;
;
 ;
;
 .
.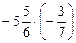 .
. .
. , если а = –1;
, если а = –1;  ; а = – 0,45.
; а = – 0,45.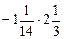 .
.
 , если п = –1;
, если п = –1;  ; п = –0,84.
; п = –0,84. .
. .
. ; 0: (–5,8) = 0.
; 0: (–5,8) = 0.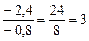 ; в)
; в)  ;
;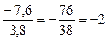 ; г)
; г)  .
. .
.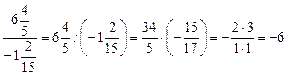 ;
; .
.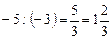 ; г)
; г)  ;
; ; д)
; д) 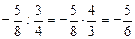 ;
; ; е)
; е)  ;
; .
.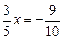 ;
;  ;
;  ; х = –1,5;
; х = –1,5; ;
;  ;
;  .
. ;
;  ;
; 
 . Ответ: х = –2,9.
. Ответ: х = –2,9. ;
; 
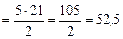 ; х = 52,5. Ответ: х = 52,5.
; х = 52,5. Ответ: х = 52,5.


