
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
I. Организация учащихся на проведение работы.
II. Выполнение контрольной работы по вариантам. Вариант 1. 1. Выполните действия:
2. За два дня было вспахано 240 га. Во второй день вспахали 3. За 4. Решите уравнение 5. Представьте в виде дроби выражение Вариант II. 1. Выполните действия:
2. В два железнодорожных вагона погрузили 117 т зерна, причем зерно второго вагона составляет 3. Масса 4. Решите уравнение 5. Представьте в виде дроби выражение Вариант III. 1. Выполните действия:
2. За два часа самолет пролетел 1020 км. За первый час он пролетел 3. За 4. Решите уравнение 5. Представьте в виде дроби выражение Вариант IV. 1. Выполните действия:
2. В двух автоцистернах 32 т бензина. Количество бензина первой цистерны составляло 3. За 4. Решите уравнение 5. Представьте в виде дроби выражение III. Итог урока. Повторить правило деления дроби на дробь (п. 17) и правило умножения обыкновенных дробей (п. 13). НАХОЖДЕНИЕ ЧИСЛА ПО ЕГО ДРОБИ Урок 1 Цель: ввести правило нахождения числа по его дроби и показать его применение при выполнении упражнений и решении задач. Ход урока I. Анализ контрольной работы. 1. Сообщить учащимся результаты контрольной работы и указать ошибки. 2. Решить на доске задания, вызвавшие затруднения у учащихся. II. Объяснение нового материала. 1. Повторить правила деления числа на дробь, деления дроби на дробь, умножения дробей. 2. Сформулировать основное свойство дроби. 3. Решить задачу 1 на странице 104 учебника. Задача 1. Расчистили от снега Ответ: 2000 м2. 4. Записать в тетрадях правило: чтобы найти число по данному значению его дроби, надо это значение разделить на дробь.
5. Разобрать решение задачи 2 на страницах 104–105 учебника. Пшеницей засеяно 2400 га, что составляет 0,8 всего поля. Найдите площадь всего поля. Решение. Так как 2400: 0,8 = 24000: 8 = 3000, то площадь всего поля равна 3000 га. Ответ: 3000 га. 6. Решить задачу 3 (решение на странице 105 учебника). III. Закрепление изученного материала. 1. Решить задачу № 647 на доске и в тетрадях. Решение. 1) 300: Ответ: 800 м. 2. Решить задачу № 648 с комментированием на месте. Решение. 1) 1,5: Ответ: 8 м. 3. Решить задачу № 650 (решение объясняет учитель). Решение. 18% = 0,18 1) 68,4: 0,18 = 6840: 18 = 380 (км/ч) средняя скорость самолета с прежним двигателем. Ответ: 380 км/ч. 4. Решить задачи самостоятельно: а) Девочка потеряла 30 бусинок, что составляло Ответ: 36 бусинок. б) Турист проплыл на байдарке 504 км, что составило 36% всего пути. Найдите длину всего пути. Решение. 36% = 0,36; 1) 504: 0,36 = 50400: 36 = 1400 (км). Ответ: 1400 км. IV. Итог урока. 1. Сформулируйте правило нахождения числа по данному значению его дроби. 2. Расскажите, как найти число по данному значению его процентов. Домашнее задание: выучить правило п. 18; решить № 680, 683, 678 (3; 4). Урок 2 Цели: способствовать выработке навыков и умений при решении задач на нахождение числа по его дроби; учить учащихся решению задач. Ход урока I. Проверка выполнения домашнего задания. 1. Двое учащихся решают на доске задачи № 680 и 683. 2. С остальными учащимися проводится устная работа: 1) сформулировать правило нахождения числа по его дроби; 2) решить задачи: а) Какова сумма денег, если 12 р. составляют б) Определите длину отрезка, в) Сыну 10 лет. Его возраст составляет 3) Решить № 671 (а). II. Выполнение упражнений. 1. Решить задачу № 649 на доске и в тетрадях. Решение. 1) 211,2: 0,88 = 21120: 88 = 240 (т) зерна намолотили за день. Ответ: 240 т. 2. Решить задачу № 651 с комментированием на месте. Решение. 1) 231: 0,55 = 23100: 55 = 420 (кг) свежей рыбы. Ответ: 420 кг. 3. Решить задачу № 656 на доске и в тетрадях.
Решение. 1) 24: 0,8 = 240: 8 = 30 (км) прошли туристы в первый день. 2) 30: Ответ: 144 км. 4. Решить задачу № 661. Решение. 1) 100% – (40% + 53%) = 100% – 93% = 7% тетрадей продано в третий день. 2) 847: 0,07 = 84700: 7 = 12100 (тетрадей) продал киоск за три дня) Ответ: 12100 тетрадей. 5. Повторение ранее изученного материала. а) Решить № 678 (1; 2). Двое учащихся решают на доске, остальные – в тетрадях, затем проверяется решение. Решение.
б) Решить задачу № 675. Решение.
2) 12,5 Ответ: 31,25 км. III. Итог урока. 1. Сформулировать правило нахождения числа по данному значению его дроби. 2. Устно решить задачу: Дочери 12 лет. Ее возраст составляет Ответ: 30 лет. 3. Рассказать, как найти число по данному значению его процентов. 4. Устно решить задачу: Найти число, если 1% его равен 85. Ответ: 8500. Домашнее задание: изучить п. 18; решить № 681, 679(2), 684, 691(а). Урок 3 Цели: закрепить правило нахождения числа по его дроби; развивать навыки решения задач; развивать логическое мышление учащихся. Ход урока I. Устная работа. 1. Повторить правило деления дроби на дробь и правило умножения дробей. 2. Сформулировать основное свойство дроби. 3. Решить устно № 674 (б; в; г) и № 668 (а). 4. Повторить правило нахождения числа по его дроби и правило нахождения дроби от числа. 5. Устно решить задачи: а) Ласточка живет 9 лет, что составляет Ответ: 30 лет. б) Кровь составляет
|
||||||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 459; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.17.68.14 (0.02 с.) |
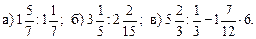
 того, что было вспахано в первый день. Сколько гектаров земли было вспахано в каждый из этих дней?
того, что было вспахано в первый день. Сколько гектаров земли было вспахано в каждый из этих дней? кг конфет заплатили
кг конфет заплатили  р. Сколько стоят
р. Сколько стоят  кг таких конфет?
кг таких конфет?
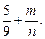

 зерна первого вагона. Сколько тонн зерна погрузили в каждый из этих вагонов?
зерна первого вагона. Сколько тонн зерна погрузили в каждый из этих вагонов?


 того пути, который он пролетел во второй час. Сколько километров пролетел самолет в каждый из этих двух часов?
того пути, который он пролетел во второй час. Сколько километров пролетел самолет в каждый из этих двух часов? кг конфет заплатили
кг конфет заплатили  р. Сколько стоят
р. Сколько стоят  кг таких конфет?
кг таких конфет?

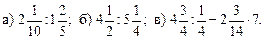
 м ткани заплатили
м ткани заплатили  р. Сколько стоят
р. Сколько стоят  м такой ткани?
м такой ткани?

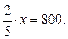 Значит,
Значит,  Площадь катка равна 2000 м2.
Площадь катка равна 2000 м2.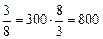 (м) длина дистанции.
(м) длина дистанции. (м) длина всей сваи.
(м) длина всей сваи. всей нити бус. Сколько бусинок было на нитке?
всей нити бус. Сколько бусинок было на нитке? которого имеют длину 15 см.
которого имеют длину 15 см.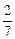 возраста отца. Сколько лет отцу?
возраста отца. Сколько лет отцу?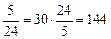 (км) намеченный путь.
(км) намеченный путь.

 (км/ч) скорость велосипедиста.
(км/ч) скорость велосипедиста. (км) путь велосипедиста.
(км) путь велосипедиста.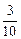 продолжительности жизни жаворонка. Сколько лет живет жаворонок?
продолжительности жизни жаворонка. Сколько лет живет жаворонок? массы тела человека. Сколько крови у человека, масса которого 65 кг?
массы тела человека. Сколько крови у человека, масса которого 65 кг?


