
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Система управління запасами з дефіцитом
У попередній моделі ми прийняли припущення, що дефіцит не допускається. Це означало повне задоволення попиту на продукт, що запасається, тобто збіг інтенсивності попиту та інтенсивності витрачання запасу. У даній моделі припустимо, що дефіцит можливий. Це означає, що при відсутності запасу товару попит зберігається з тією ж інтенсивністю b(t), що і раніше, але споживання запасу нема, у наслідок чого накопичується дефіцит. Очевидно, що якщо дефіцит у системі не приводив би до додаткових витрат, пов’язаних із можливими штрафами або втратою прибутку, то оптимально було б не мати взагалі наявного запасу. З іншого боку, якщо ці витрати досить великі, то взагалі не слід допускати дефіциту. При проміжних значеннях витрат, пов’язаних із дефіцитом, оптимально допустити його у кінці циклу. Припустимо, що інтенсивність попиту b(t), вартість поповнення запасу Модель 1. Введемо позначення: Q – загальний обсяг споживання товару протягом часу Т; q – обсяг поставки;
s – максимальний рівень запасу;
Інші параметри моделі мають такий же смисл, як і в попередній моделі. Графік зміни рівня запасу представлений на рисунку 2.3.
Рис. 2.3. Зміна рівня запасу Припустимо, що в момент перед поставкою поповнення запасу в системі кожний раз є дефіцит у
Убування графіка нижче осі абсцис в область від’ємних значень характеризує накопичення дефіциту. На рисунку 2.3 видно, що кожний період
В даній моделі у функцію сумарних витрат C (витрат за період T) поряд з витратами
Витрати
Витрати на зберігання середнього запасу за час споживання
Відповідно ці витрати за період T складуть
При розрахунку витрат
Тепер загальні витрати за формулою
Неважко помітити, що при q = s формула (2.15) співпадає з раніш одержаною формулою (2.4) в моделі без дефіциту. Таким чином, задача управління запасами в моделі з дефіцитом зводиться до пошуку такого обсягу партії q і максимального рівня запасу s, при яких функція витрат С(q, s) приймає мінімальне значення. Іншими словами, необхідно дослідити функцію двох змінних
Розв’язавши цю систему відносно q і s, отримаємо формули найбільш економічного обсягу партії
Величина
називається щільністю збитків через незадоволення попиту та відіграє важливу роль в аналізі систем управління запасами. Відмітимо, що в реальних системах управління запасами Недопустимість дефіциту ототожнюється з припущенням, що
Враховуючи (2.16) і (2.17) можна записати
Тому твердження про те, що щільність збитків у наслідок незадовільненого попиту дорівнює
Одержувана звідси формула
дозволяє оцінити Із формул (2.6) і (2.16) випливає, що оптимальні обсяги партій для моделі з дефіцитом
Це означає, що оптимальний обсяг партії в моделі з дефіцитом у У цій моделі, як і у попередніх, ми припускали, що поставки здійснюються миттєво в момент подачі замовлення. Якщо припустити, що поставка здійснюється з деякою затримкою
В принципі точку замовлення у даній моделі визначають таким же чином, як і в розділі 2.1. Але треба по-новому визначити поняття “рівень запасів”. Поняття “наявний запас” вже не годиться, тому що в момент подачі замовлення наявний запас може бути відсутнім, а враховані замовлення можуть бути. Зручно замінити наявний запас різницею наявного запасу і обсягу врахованих вимог, яка називається чистим запасом. Якщо є наявний запас, то врахованих вимог не буде і чистий запас буде додатним. Якщо є враховані вимоги, то не буде наявного запасу, а чистий запас буде від’ємним. При використанні поняття чистого запасу точка замовлення буде дорівнювати
де m означає найбільше ціле число, менше або рівне Приклад 2.4. Визначимо оптимальний розмір партії, максимальний рівень запасу, оптимальну кількість поставок і оптимальний інтервал часу між поставками для моделі з дефіцитом за даними прикладу 2.3. Введемо додаткову умову, що відсутність на складі потрібного товару приносить збиток у розмірі 3,5 грн. на одиницю товару. Визначимо також: a) на скільки відсотків збільшаться витрати на створення і зберігання запасу в обсязі Розв’язання. За умовою задачі Q=3650, T=365,
Алгоритм реалізації моделі v задаємо початкові значення параметрів моделі v визначаємо інтенсивність витрачання запасів b, записуємо формули для кількості поставок k і інтервалу часу між поставками v записуємо функції витрат v визначаємо оптимальний обсяг поставки v визначаємо мінімальне значення функції витрат v визначаємо відносну зміну витрат, коли розмір замовлення v визначаємо точку замовлення Алгоритм у Mathcad
Абсолютна і відносна зміна розміру партії постачання запасу
Абсолютна і відносна зміна витрат
Точка замовлення h, коли строк поставки u не дорівнює оптимальному
Розрахунок параметрів даної моделі дає нам інформацію про найбільш економічно вигідний обсяг запасу деталей на складі. Дефіцит деталей на складі призводить до збитків у вигляді штрафу за дефіцит. Коментар. Дані розрахунки показують, що щільність збитків із-за незадоволеного попиту дорівнює ρ = 0,91, найбільш економічний розмір поставки партії деталей становить Відносна зміна сумарних витрат при збільшенні замовлення на Модель 2. Дана модель є подальшим узагальненням попередньої моделі на випадок, коли функція витрат на поповнення запасу і функція інтенсивності споживання запасу є лінійними функціями відповідно часу t і обсягу поставки q: Сумарні витрати на постачання, як і раніше, дорівнюють
де Обсяг витраченого товару за час t дорівнює
Час Таким чином, витрати на зберігання запасу за період функціонування системи T, з урахуванням кількості поставок
Визначимо інтенсивність накопичення дефіциту як величину, пропорційну інтенсивності витрати запасу: Таким чином витрати, пов’язані з дефіцитом, за період Т функціонування системи, дорівнюють
Враховуючи формули для
Знаходячи частинні похідні від функції Сq, s) по q і s і розв’язуючи систему рівнянь
визначаємо оптимальні значення розміру партії постачання і максимального рівня запасу відповідно Розв’язання системи рівнянь здійснюємо за функцією Minerr(q, s) у блоці алгоритму, який задається директивою Given. Мінімальне значення функції Приклад 2.5. Визначимо оптимальний розмір партії постачання, максимальний рівень запасу, а також оптимальну кількість поставок і оптимальний інтервал часу між поставками для моделі з дефіцитом з додатковою умовою, що попит Розв’язання. Маємо такі значення вхідних величин:
Алгоритм реалізації моделі v задаємо початкові значення параметрів моделі v визначаємо функції v визначаємо рівень запасу v визначаємо час вичерпання запасу u(s), розв’язуючи рівняння v визначаємо час v визначаємо функцію витрат
v розв’язуємо систему рівнянь D1(q, s) = 0, D2(q, s) = 0 і визначаємо значення v визначаємо оптимальну кількість поставок v визначаємо мінімальне значення функції витрат Алгоритм у Mathcad
Рівень запасу в момент часу t;
Час накопичення дефіциту до рівня Функція витрат
Розв’язання системи рівнянь D1(q, s) = 0 і D2(q, s) = 0 і визначення оптимального обсягу поставки, оптимального рівня запасу, оптимальної кількості поставок і часу між поставками
Мінімальне значення функції витрат
Коментар. Оптимальна політика управління запасами наступна: оптимальний розмір поставки
Модель 3. У даній моделі приймемо, що витрати Витрати на поповнення і зберігання запасу, як і в моделі 1, дорівнюють
Витрати у наслідок дефіциту за цикл дорівнюють
де враховано, що За період T ці витрати складають
Середні сумарні витрати за період Т, які включають витрати на постачання і утримання запасу, а також витрати, пов’язані з дефіцитом запасу дорівнюють
тобто
Задача полягає у тому, щоб визначити обсяг поставки q і максимальний рівень запасів s, при яких загальні витрати були б мінімальні.
Розглянемо тепер алгоритм розв’язання цієї системи рівнянь. Із (2.22) одержуємо
Після перетворень цього виразу, одержимо
або
Далі маємо
Звідки
Одержали наступну систему рівнянь
Розв’язуючи систему, одержуємо формули для найбільш економічного обсягу партії
Величина
і збігаються із формулами (2.17) і (2.18). Визначивши
Чисельний розв’язок системи рівнянь (2.23) можна також одержати за допомогою функції Mathcad Minerr(q, s), застосовуючи блок розв’язання Given. Відповідний алгоритм наведемо при розв’язанні прикладу 2.6. Крім того, засоби Mathcad дозволяють одержати систему рівнянь, аналогічну (2.23), у неявному вигляді за допомогою операцій символьного диференціювання. Приклад 2.6. Розглянемо систему управління запасами із наступними характеристиками: обсяг замовлень Q = 200 одиниць на рік; вартість створення одиниці запасу c1 = 500 грош. од.; коефіцієнт витрат утримання запасів І = 0,1 (розмірність – вартість в одиницю часу на одиницю капіталу, вкладеного в запаси); вартість утримання одиниці запасів Визначимо оптимальний обсяг поставки Розв’язання. Розглянемо два алгоритми визначення величин Алгоритм реалізації моделі у Mathcad аналогічний попередньому алгоритму. Алгоритм у Mathcad
|
|||||||||
|
Последнее изменение этой страницы: 2017-02-10; просмотров: 162; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.42.94 (0.137 с.) |
 , витрати на зберігання запасу
, витрати на зберігання запасу  і витрати у наслідок дефіциту
і витрати у наслідок дефіциту  задані у вигляді наступних функцій:
задані у вигляді наступних функцій: 
 ,
, 
 , де t – час, q – обсяг партії поповнення запасу. У загальному випадку вказані функції включають постійні складові і складові, пропорційні часу або обсягу поставки. Зокрема, витрати з урахуванням дефіциту, пропорційні часу відсутності запасу при наявності попиту.
, де t – час, q – обсяг партії поповнення запасу. У загальному випадку вказані функції включають постійні складові і складові, пропорційні часу або обсягу поставки. Зокрема, витрати з урахуванням дефіциту, пропорційні часу відсутності запасу при наявності попиту.
 інтенсивність витрачання запасу;
інтенсивність витрачання запасу; – обсяг дефіциту (кількість незадовільнених вимог, зареєстрованих до моменту поставки);
– обсяг дефіциту (кількість незадовільнених вимог, зареєстрованих до моменту поставки); – інтервал часу, коли в системі є наявний запас;
– інтервал часу, коли в системі є наявний запас;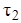 – інтервал часу, протягом якого у системі є дефіцит товару;
– інтервал часу, протягом якого у системі є дефіцит товару; – витрати на створення або поставку однієї партії товару, які не залежать від її обсягу, грош. од.;
– витрати на створення або поставку однієї партії товару, які не залежать від її обсягу, грош. од.; – витрати на зберігання одиниці запасу в од. часу, грош. од.;
– витрати на зберігання одиниці запасу в од. часу, грош. од.; – витрати, пов’язані з дефіцитом запасу, грош. од.
– витрати, пов’язані з дефіцитом запасу, грош. од.
 незадоволених вимог. Після поставки поповнення в обсязі q одиниць ці
незадоволених вимог. Після поставки поповнення в обсязі q одиниць ці 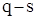 вимог негайно задовольняються і наявний запас у системі складе s одиниць.
вимог негайно задовольняються і наявний запас у системі складе s одиниць. розбивається на два часових інтервали, тобто
розбивається на два часових інтервали, тобто  , де
, де  – час, протягом якого відбувається споживання запасу,
– час, протягом якого відбувається споживання запасу, 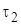 – час, коли запас відсутній і накопичується дефіцит, який буде покритий в момент надходження наступної партії. Із графіка легко встановити, що
– час, коли запас відсутній і накопичується дефіцит, який буде покритий в момент надходження наступної партії. Із графіка легко встановити, що
 на поповнення запасу і витратами
на поповнення запасу і витратами  на зберігання запасу необхідно ввести витрати
на зберігання запасу необхідно ввести витрати  , пов’язані із дефіцитом. Тоді функція витрат дорівнюватиме
, пов’язані із дефіцитом. Тоді функція витрат дорівнюватиме
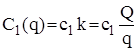 .
. дорівнюють
дорівнюють .
.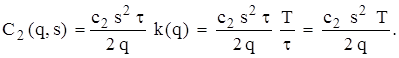
 . Оскільки середній рівень дефіциту за період
. Оскільки середній рівень дефіциту за період  дорівнює
дорівнює  то витрати за цей період складуть
то витрати за цей період складуть  а за весь період T з урахуванням (2.3) дорівнюватимуть
а за весь період T з урахуванням (2.3) дорівнюватимуть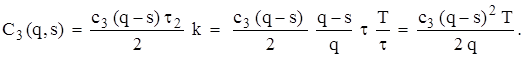
 дорівнюють
дорівнюють (2.15)
(2.15) на екстремум. Прирівнюючи частинні похідні
на екстремум. Прирівнюючи частинні похідні 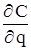 та
та 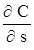 до нуля, після перетворень одержимо систему рівнянь
до нуля, після перетворень одержимо систему рівнянь
 і максимального рівня запасу
і максимального рівня запасу 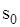 для моделі з дефіцитом.
для моделі з дефіцитом. , (2.16)
, (2.16) (2.17)
(2.17) (2.18)
(2.18)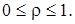 Якщо значення
Якщо значення  мале у порівнянні з
мале у порівнянні з  значно більше
значно більше  , то ρ близька до 1.
, то ρ близька до 1. або
або 
 та
та  .
. означає, що впродовж ρ100% часу від повного періоду τ система буде бездефіцитна, а впродовж (1–ρ)100% часу запас буде відсутній. У ймовірнісних термінах це означає, що ймовірність вичерпання запасів дорівнює
означає, що впродовж ρ100% часу від повного періоду τ система буде бездефіцитна, а впродовж (1–ρ)100% часу запас буде відсутній. У ймовірнісних термінах це означає, що ймовірність вичерпання запасів дорівнює
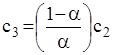 (2.19)
(2.19)
 і моделі без дефіциту
і моделі без дефіциту  (обчислений за формулою Уілсона), пов’язані співвідношенням
(обчислений за формулою Уілсона), пов’язані співвідношенням (2.20)
(2.20) раз більше ніж в моделі без дефіциту.
раз більше ніж в моделі без дефіциту. то замовлення на поставку товарів повинно здійснюватись при зниженні запасу до рівня, який би давав можливість задовольняти попит на товари протягом часу
то замовлення на поставку товарів повинно здійснюватись при зниженні запасу до рівня, який би давав можливість задовольняти попит на товари протягом часу 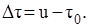 Визначаючи щоденну потребу в товарі (інтенсивність витрати запасу) за формулою (2.1), рівень запасу
Визначаючи щоденну потребу в товарі (інтенсивність витрати запасу) за формулою (2.1), рівень запасу 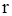 , при якому робиться замовлення обчислюємо за формулою
, при якому робиться замовлення обчислюємо за формулою .
. ,
, де u – час поставки,
де u – час поставки, 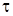 – тривалість циклу,
– тривалість циклу,  = b u – обсяг попиту за час поставки (тобто кількість замовлених одиниць товару з моменту подачі замовлення і до моменту поставки),
= b u – обсяг попиту за час поставки (тобто кількість замовлених одиниць товару з моменту подачі замовлення і до моменту поставки), 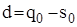 – обсяг дефіциту. Величина
– обсяг дефіциту. Величина 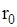 може приймати від’ємні значення. З іншого боку, це означає, що замовлення подається в момент, коли обсяг врахованих вимог досягає величини
може приймати від’ємні значення. З іншого боку, це означає, що замовлення подається в момент, коли обсяг врахованих вимог досягає величини  . Сума наявного запасу і замовленого товару замінюється тепер сумою наявного запасу мінус обсяг врахованих замовлень при дефіциті товару. Ця сума називається фіктивним рівнем запасів у системі. При використанні фіктивного рівня запасів точка замовлення дорівнює
. Сума наявного запасу і замовленого товару замінюється тепер сумою наявного запасу мінус обсяг врахованих замовлень при дефіциті товару. Ця сума називається фіктивним рівнем запасів у системі. При використанні фіктивного рівня запасів точка замовлення дорівнює  , причому
, причому 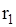 може приймати також від’ємні значення.
може приймати також від’ємні значення. що замовляється, відмінного від оптимального розміру
що замовляється, відмінного від оптимального розміру  днів.
днів.
 ,
,  ,
, 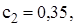
 ,
, 
 .
.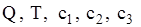 і обчислюємо щільність збитків
і обчислюємо щільність збитків  ;
; ;
; і функцію загальних витрат
і функцію загальних витрат  ;
; кількість партій постачання
кількість партій постачання  і довжину інтервалу між послідовними замовленнями на поповнення запасу
і довжину інтервалу між послідовними замовленнями на поповнення запасу 
 ;
; відрізняється від оптимального
відрізняється від оптимального  ;
;


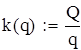







 грош. од.
грош. од.




 деталей, максимальний рівень запасу
деталей, максимальний рівень запасу  одиниць, кількість замовлень
одиниць, кількість замовлень  , інтервал між замовленнями
, інтервал між замовленнями  доба. Сумарні витрати на зберігання запасу дорівнюють
доба. Сумарні витрати на зберігання запасу дорівнюють  грош. од.
грош. од.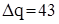 одиниць дорівнює
одиниць дорівнює  . Точка замовлення партії, якщо її поставка затримується на
. Точка замовлення партії, якщо її поставка затримується на  днів дорівнює
днів дорівнює  одиниць. ▲
одиниць. ▲
 ,
,  можуть бути визначені на основі експериментальних даних у вигляді рівнянь регресії.
можуть бути визначені на основі експериментальних даних у вигляді рівнянь регресії. ,
, .
. . Обсяг товару, що зберігається на складі в момент t, дорівнює різниці між обсягом запасу на початку періоду і обсягом витраченого товару за час t:
. Обсяг товару, що зберігається на складі в момент t, дорівнює різниці між обсягом запасу на початку періоду і обсягом витраченого товару за час t: 
 за який відбувається повне вичерпання запасу знаходиться із рівняння
за який відбувається повне вичерпання запасу знаходиться із рівняння 
 , дорівнюють
, дорівнюють
 де коефіцієнт a визначає частку попиту b(t), який враховується. Тоді, оскільки дефіцит товару на момент часу t дорівнює величині z(t), то миттєві штрафні витрати за дефіцит у цей момент дорівнюють
де коефіцієнт a визначає частку попиту b(t), який враховується. Тоді, оскільки дефіцит товару на момент часу t дорівнює величині z(t), то миттєві штрафні витрати за дефіцит у цей момент дорівнюють  . Час
. Час  за який відбувається накопичення дефіциту до величини
за який відбувається накопичення дефіциту до величини  визначається із рівняння
визначається із рівняння  .
.
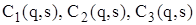 і рівність k(q) =Q/q, загальні витрати за період T дорівнюватимуть
і рівність k(q) =Q/q, загальні витрати за період T дорівнюватимуть
 (2.21)
(2.21)
 і
і  які доставляють мінімум функції
які доставляють мінімум функції 
 знаходимо, підставляючи в неї значення
знаходимо, підставляючи в неї значення  , одержуємо
, одержуємо  .
. на продукцію при відсутності запасу, є лінійною функцією часу і пропорційний функції споживання запасу при його наявності, тобто
на продукцію при відсутності запасу, є лінійною функцією часу і пропорційний функції споживання запасу при його наявності, тобто  де a
де a  – коефіцієнт пропорційності, який визначає кількість врахованих заявок на товар при його відсутності.
– коефіцієнт пропорційності, який визначає кількість врахованих заявок на товар при його відсутності.


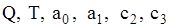

 ;
; в момент часу t;
в момент часу t; Розв’язання здійснюємо за оператором solve;
Розв’язання здійснюємо за оператором solve;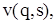 за який відбувається накопичення дефіциту до рівня q – s, розв’язуючи рівняння
за який відбувається накопичення дефіциту до рівня q – s, розв’язуючи рівняння 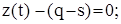
 і її частинні похідні
і її частинні похідні ,
,  ;
; при яких функція витрат
при яких функція витрат 
 .
.




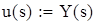







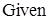





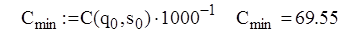 грош. од.
грош. од. одиниць, максимальний рівень запасу
одиниць, максимальний рівень запасу  одиниць, кількість замовлень
одиниць, кількість замовлень  . Пропорційно зменшенню частоти поставок
. Пропорційно зменшенню частоти поставок  у порівнянні з моделлю без дефіциту, зменшився інтервал часу між поставками, який дорівнює
у порівнянні з моделлю без дефіциту, зменшився інтервал часу між поставками, який дорівнює  доби. Мінімальне значення функції витрат дорівнює
доби. Мінімальне значення функції витрат дорівнює  грош. од. ▲
грош. од. ▲

 , пов’язані з дефіцитом запасу, включають постійну складову
, пов’язані з дефіцитом запасу, включають постійну складову 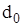 і складову
і складову  пропорційну тривалості дефіциту.
пропорційну тривалості дефіциту.


 .
. .
. ,
, . (2.22)
. (2.22) Оскільки функція С(q, s) диференційовна у всій області її визначення, то
Оскільки функція С(q, s) диференційовна у всій області її визначення, то  і
і  повинні задовольняти рівнянням
повинні задовольняти рівнянням


 .
. .
. .
. (2.23)
(2.23) і максимального рівня запасів
і максимального рівня запасів  для моделі з дефіцитом, втрати від якого пропорційні часу відсутності запасів
для моделі з дефіцитом, втрати від якого пропорційні часу відсутності запасів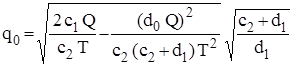 (2.24)
(2.24) (2.25)
(2.25) дорівнює розміру дефіциту. Коли коефіцієнт
дорівнює розміру дефіциту. Коли коефіцієнт  , формули (2.23) і (2.24) мають вигляд:
, формули (2.23) і (2.24) мають вигляд:

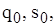 визначаємо інші параметри системи:
визначаємо інші параметри системи:
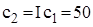 грош. од.; витрати у наслідок втрати замовлення без врахування втраченого прибутку
грош. од.; витрати у наслідок втрати замовлення без врахування втраченого прибутку  грош. од.; витрати, пропорційні тривалості дефіциту
грош. од.; витрати, пропорційні тривалості дефіциту  грош. од.; період роботи системи
грош. од.; період роботи системи  рік; час поставки поповнення запасу t = 9 місяців.
рік; час поставки поповнення запасу t = 9 місяців. оптимальний рівень запасів
оптимальний рівень запасів  кількість поставок
кількість поставок 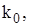 час між поставками
час між поставками  точку замовлення
точку замовлення  , виходячи із фіктивного рівня запасів, точку замовлення
, виходячи із фіктивного рівня запасів, точку замовлення 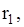 виходячи із рівня чистого запасу і обсяг дефіциту
виходячи із рівня чистого запасу і обсяг дефіциту  .
.





