
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Розділ 2. Детерміновані моделіСтр 1 из 8Следующая ⇒
РОЗДІЛ 2. ДЕТЕРМІНОВАНІ МОДЕЛІ УПРАВЛІННЯ ЗАПАСАМИ Алгоритм у Mathcad. Вхідні дані моделі
Визначення оптимального обсягу поставки
Рис. 2.2. Графіки функцій Мінімальне значення функції витрат
Припустимо тепер, що в умовах попередньої моделі замовляються не всі партії зразу, а кожна окремо, причому термін виконання замовлення дорівнює 60 дням. Визначимо точку замовлення, тобто при якому рівні запасу слід замовляти наступну партію. Оскільки за результатом розв’язання попередньої задачі довжина інтервалу між поставками дорівнює 54 дням, то замовлення в умовах стабільної роботи торгівельного підприємства слід поновити, коли рівень запасу буде достатній для задовільнення потреби на
Оскільки щоденна потреба (інтенсивність витрати запасу) за формулою (2.1) дорівнює
Коментар. Оптимальна стратегія управління запасами може бути сформульована наступним чином: найбільш економічний обсяг партії дорівнює Зауважимо, що у Mathcad екстремальне значення будь-якої величини (наприклад, максимальне або мінімальне значення) можна також визначити і графічно. Для того, щоб визначити по графіку значення потрібної величини, клацніть у меню Алгоритм реалізації моделі v задаємо вхідні дані моделі v записуємо вирази для кількості поставок v визначаємо функції витрат vзастосовуючи оператор диференціювання, знаходимо похідну v розв’язуючи рівняння v визначаємо оптимальну кількість поставок v визначаємо мінімальне значення функції витрат Алгоритм у Mathcad
Коментар. Одержали такі результати: розмір найбільш економічної поставки дорівнює Модель 2 Обсяг витраченого товару за час t дорівнює b(t), обсяг товару, який зберігається на складі в момент t дорівнює різниці між розміром поставки на початку періоду і обсягом витраченого товару за час t: Миттєві витрати в момент часу t дорівнюють Якщо врахувати, що кількість партій постачання дорівнює
Знаходячи похідну від функції C(q) по q – Оптимальну кількість поставок Приклад 2.3. Розглянемо складську систему із наступними параметрами: інтенсивність витрачання запасу і витрати на постачання є лінійними функціями відповідно часу і обсягу партії постачання q: Визначимо, як і раніше, найбільш економічний розмір партії товарів Розв’язання. Позначаючи довжину періоду, у якому витрачається черговий запас, замість τ через u(q), алгоритм буде мати наступний вигляд. Алгоритм реалізації моделі v задаємо початкові значення параметрів моделі: v записуємо вирази для визначення інтенсивності витрачання запасу b(t), кількості поставок k(q) і інтервалу часу між поставками τ(q); v визначаємо рівень запасу в момент часу t
v визначаємо функції витрат v знаходимо похідну від функції v визначаємо оптимальний розмір партії постачання v визначаємо оптимальну кількість поставок v визначаємо мінімальне значення функції витрат Алгоритм у Mathcad
Коментар. Оптимальна стратегія управління запасами у даній моделі передбачає такі значення параметрів системи: розмір найбільш економічної партії поставки дорівнює Алгоритм реалізації моделі v задаємо початкові значення параметрів моделі v визначаємо інтенсивність витрачання запасів b, записуємо формули для кількості поставок k і інтервалу часу між поставками v записуємо функції витрат v визначаємо оптимальний обсяг поставки v визначаємо мінімальне значення функції витрат v визначаємо відносну зміну витрат, коли розмір замовлення v визначаємо точку замовлення Алгоритм у Mathcad
Абсолютна і відносна зміна розміру партії постачання запасу
Абсолютна і відносна зміна витрат
Точка замовлення h, коли строк поставки u не дорівнює оптимальному
Розрахунок параметрів даної моделі дає нам інформацію про найбільш економічно вигідний обсяг запасу деталей на складі. Дефіцит деталей на складі призводить до збитків у вигляді штрафу за дефіцит. Коментар. Дані розрахунки показують, що щільність збитків із-за незадоволеного попиту дорівнює ρ = 0,91, найбільш економічний розмір поставки партії деталей становить Відносна зміна сумарних витрат при збільшенні замовлення на Модель 2. Дана модель є подальшим узагальненням попередньої моделі на випадок, коли функція витрат на поповнення запасу і функція інтенсивності споживання запасу є лінійними функціями відповідно часу t і обсягу поставки q: Сумарні витрати на постачання, як і раніше, дорівнюють
де Обсяг витраченого товару за час t дорівнює
Час Таким чином, витрати на зберігання запасу за період функціонування системи T, з урахуванням кількості поставок
Визначимо інтенсивність накопичення дефіциту як величину, пропорційну інтенсивності витрати запасу: Таким чином витрати, пов’язані з дефіцитом, за період Т функціонування системи, дорівнюють
Враховуючи формули для
Знаходячи частинні похідні від функції Сq, s) по q і s і розв’язуючи систему рівнянь
визначаємо оптимальні значення розміру партії постачання і максимального рівня запасу відповідно Розв’язання системи рівнянь здійснюємо за функцією Minerr(q, s) у блоці алгоритму, який задається директивою Given. Мінімальне значення функції Приклад 2.5. Визначимо оптимальний розмір партії постачання, максимальний рівень запасу, а також оптимальну кількість поставок і оптимальний інтервал часу між поставками для моделі з дефіцитом з додатковою умовою, що попит Розв’язання. Маємо такі значення вхідних величин:
Алгоритм реалізації моделі v задаємо початкові значення параметрів моделі v визначаємо функції v визначаємо рівень запасу v визначаємо час вичерпання запасу u(s), розв’язуючи рівняння v визначаємо час v визначаємо функцію витрат
v розв’язуємо систему рівнянь D1(q, s) = 0, D2(q, s) = 0 і визначаємо значення
v визначаємо оптимальну кількість поставок v визначаємо мінімальне значення функції витрат Алгоритм у Mathcad
Рівень запасу в момент часу t;
Час накопичення дефіциту до рівня Функція витрат
Розв’язання системи рівнянь D1(q, s) = 0 і D2(q, s) = 0 і визначення оптимального обсягу поставки, оптимального рівня запасу, оптимальної кількості поставок і часу між поставками
Мінімальне значення функції витрат
Коментар. Оптимальна політика управління запасами наступна: оптимальний розмір поставки Модель 3. У даній моделі приймемо, що витрати Витрати на поповнення і зберігання запасу, як і в моделі 1, дорівнюють
Витрати у наслідок дефіциту за цикл дорівнюють
де враховано, що За період T ці витрати складають
Середні сумарні витрати за період Т, які включають витрати на постачання і утримання запасу, а також витрати, пов’язані з дефіцитом запасу дорівнюють
тобто
Задача полягає у тому, щоб визначити обсяг поставки q і максимальний рівень запасів s, при яких загальні витрати були б мінімальні.
Розглянемо тепер алгоритм розв’язання цієї системи рівнянь. Із (2.22) одержуємо
Після перетворень цього виразу, одержимо
або
Далі маємо
Звідки
Одержали наступну систему рівнянь
Розв’язуючи систему, одержуємо формули для найбільш економічного обсягу партії
Величина
і збігаються із формулами (2.17) і (2.18). Визначивши
Чисельний розв’язок системи рівнянь (2.23) можна також одержати за допомогою функції Mathcad Minerr(q, s), застосовуючи блок розв’язання Given. Відповідний алгоритм наведемо при розв’язанні прикладу 2.6. Крім того, засоби Mathcad дозволяють одержати систему рівнянь, аналогічну (2.23), у неявному вигляді за допомогою операцій символьного диференціювання. Приклад 2.6. Розглянемо систему управління запасами із наступними характеристиками: обсяг замовлень Q = 200 одиниць на рік; вартість створення одиниці запасу c1 = 500 грош. од.; коефіцієнт витрат утримання запасів І = 0,1 (розмірність – вартість в одиницю часу на одиницю капіталу, вкладеного в запаси); вартість утримання одиниці запасів
Визначимо оптимальний обсяг поставки Розв’язання. Розглянемо два алгоритми визначення величин Алгоритм реалізації моделі у Mathcad аналогічний попередньому алгоритму. Алгоритм у Mathcad
Алгоритм реалізації моделі v задаємо вхідні дані моделі v послідовно обчислюємо величини v визначаємо мінімальне значення цільової функції v застосовуючи функцію Mathcad floor(), визначаємо найбільше ціле число m, яке менше або рівне величині Алгоритм у Mathcad
Коментар. Отже при обмеженій продуктивності виробництва продукції оптимальний розмір партії дорівнює Управління запасами Розглянемо модель системи управління запасами з постійною інтенсивністю попиту Ведемо позначення:1
Позначимо також через Динаміка зміни рівня запасу у системі представлена на рис. 2.7.
Рис. 2.7.
Рис. 2.7. Графік зміни рівня запасу Рівень запасу у системі визначається таким співвідношенням:
Припускаючи витрати на зберігання запасу і штрафи пропорційними середньому запасу і часу існування дефіциту, для функції витрат за цикл одержимо
Максимальний дефіцит
Із рис 2.7 видно, що
Підставивши ці значення у вираз для
Перепишемо функцію витрат з урахуванням лінійності зміни рівня запасу:
У розгорнутому вигляді маємо
Усереднюючи цей вираз по
Знайдемо частинні похідні від
Розв’язання цієї системи рівнянь дає оптимальні значення величин
При цьому досягається мінімум витрат в одиницю часу
Момент запуску виробництва визначається досягненням дефіциту
Із одержаних співвідношень як частинні випадки можна одержати деякі відомі формули теорії запасів. Так, наприклад, при високому штрафі за дефіцит можна прийняти
Інший частинний випадок відповідає високій інтенсивності поповнення запасу
При виконанні обох умов одержуються відомі формули Уілсона
Окрім розглянутих вище показників, інтерес представляють ще два – найбільш економічний обсяг парті, що замовляється
|
||||||||||||||
|
Последнее изменение этой страницы: 2017-02-10; просмотров: 151; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.14.240.178 (0.2 с.) |

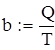










 :
: 
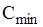
 грош. од.
грош. од. днів.
днів.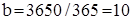 одиницям товару, то замовлення повинні робитись при досягненні рівня запасу до
одиницям товару, то замовлення повинні робитись при досягненні рівня запасу до 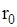 одиниць:
одиниць:
 одиниць, кількість поставок у рік
одиниць, кількість поставок у рік  , інтервал між поставками
, інтервал між поставками  дня. Мінімальне значення функції витрат на поставку і зберігання товару при вказаних значеннях
дня. Мінімальне значення функції витрат на поставку і зберігання товару при вказаних значеннях  і
і  дорівнює
дорівнює 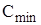 = 68,3 грош. од.
= 68,3 грош. од. (Формат) у пункті
(Формат) у пункті  (Графік) по рядку
(Графік) по рядку  (Слідування), встановіть перехрестя маркера на потрібній точці графіка і виведіть у робочий документ значення
(Слідування), встановіть перехрестя маркера на потрібній точці графіка і виведіть у робочий документ значення  , які вказані у вікнах
, які вказані у вікнах  (Величина Х) і
(Величина Х) і  (Величина
(Величина  ). ▲
). ▲
 і інтервалу часу між поставками
і інтервалу часу між поставками  ;
; і функцію загальних витрат
і функцію загальних витрат  ;
; від функції
від функції  за допомогою функції Mathcad
за допомогою функції Mathcad  , визначаємо оптимальний розмір партії постачання
, визначаємо оптимальний розмір партії постачання  ;
; і інтервал часу між поставками
і інтервал часу між поставками 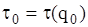 для значення
для значення  ;
; .
.






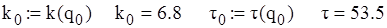
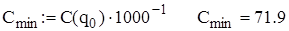 грош. од.
грош. од. Інтервал часу між поставками дорівнює
Інтервал часу між поставками дорівнює 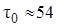 доби. Загальні витрати збільшились і дорівнюють 71,9 грош. од. Це сталось у наслідок того, що у витратах на поставку враховується розмір поставки, що збільшує ці витрати. ▲
доби. Загальні витрати збільшились і дорівнюють 71,9 грош. од. Це сталось у наслідок того, що у витратах на поставку враховується розмір поставки, що збільшує ці витрати. ▲
 .
. а час
а час  , за який буде повністю вичерпано запас, є функцією від q і визначається із рівняння
, за який буде повністю вичерпано запас, є функцією від q і визначається із рівняння 
 , то загальні витрати за період u(q) дорівнюють
, то загальні витрати за період u(q) дорівнюють . (2.14)
. (2.14) , одержуємо точку
, одержуємо точку  , яка є точкою мінімуму функції C(q). Оптимальне значення функції C(q) знаходимо, підставляючи в неї значення
, яка є точкою мінімуму функції C(q). Оптимальне значення функції C(q) знаходимо, підставляючи в неї значення  , одержуємо
, одержуємо  Значення
Значення 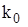 і оптимальний інтервал часу між поставками
і оптимальний інтервал часу між поставками  і
і  Для параметрів
Для параметрів  візьмемо ті ж числові дані, що і в прикладі 2.2: Q=3650, T=365,
візьмемо ті ж числові дані, що і в прикладі 2.2: Q=3650, T=365, 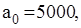
 ,
, 

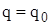 , який мінімізує функцію витрат C(q), а також обчислимо кількість поставок
, який мінімізує функцію витрат C(q), а також обчислимо кількість поставок  та інтервал часу між поставками
та інтервал часу між поставками 


 і момент вичерпання запасу
і момент вичерпання запасу 
 і функцію загальних витрат
і функцію загальних витрат 

 ,q) рівняння
,q) рівняння 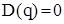 ;
; і інтервал часу між поставками
і інтервал часу між поставками  за формулами (2.3), підставляючи в них значення
за формулами (2.3), підставляючи в них значення  ;
;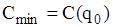 грош. од.
грош. од.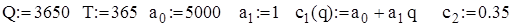








 грош. од.
грош. од. одиниць, частота замовлень дорівнює
одиниць, частота замовлень дорівнює  разів на рік, відповідний інтервал часу між поставками дорівнює
разів на рік, відповідний інтервал часу між поставками дорівнює  доби. Загальні витрати на постачання і зберігання запасу складають
доби. Загальні витрати на постачання і зберігання запасу складають  грош. од. ▲
грош. од. ▲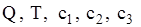 і обчислюємо щільність збитків
і обчислюємо щільність збитків  ;
; ;
; і функцію загальних витрат
і функцію загальних витрат  ;
;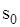 , оптимально допустимий обсяг дефіциту
, оптимально допустимий обсяг дефіциту  кількість партій постачання
кількість партій постачання  і довжину інтервалу між послідовними замовленнями на поповнення запасу
і довжину інтервалу між послідовними замовленнями на поповнення запасу 
 ;
; відрізняється від оптимального
відрізняється від оптимального 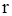 , коли строк поставки не дорівнює оптимальному.
, коли строк поставки не дорівнює оптимальному.


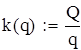







 грош. од.
грош. од.




 деталей, максимальний рівень запасу
деталей, максимальний рівень запасу  одиниць, кількість замовлень
одиниць, кількість замовлень  , інтервал між замовленнями
, інтервал між замовленнями  доба. Сумарні витрати на зберігання запасу дорівнюють
доба. Сумарні витрати на зберігання запасу дорівнюють  грош. од.
грош. од.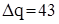 одиниць дорівнює
одиниць дорівнює  . Точка замовлення партії, якщо її поставка затримується на
. Точка замовлення партії, якщо її поставка затримується на  днів дорівнює
днів дорівнює  одиниць. ▲
одиниць. ▲
 ,
,  . Функція накопичення дефіциту z(t) є також лінійною функцією часу. Припускається, що дефіцит пропорційний попиту із заданим коефіцієнтом a, який визначається як частка врахованих вимог. Усі інші параметри моделі зберігають свій смисл. Функції
. Функція накопичення дефіциту z(t) є також лінійною функцією часу. Припускається, що дефіцит пропорційний попиту із заданим коефіцієнтом a, який визначається як частка врахованих вимог. Усі інші параметри моделі зберігають свій смисл. Функції  можуть бути визначені на основі експериментальних даних у вигляді рівнянь регресії.
можуть бути визначені на основі експериментальних даних у вигляді рівнянь регресії. ,
, .
. . Обсяг товару, що зберігається на складі в момент t, дорівнює різниці між обсягом запасу на початку періоду і обсягом витраченого товару за час t:
. Обсяг товару, що зберігається на складі в момент t, дорівнює різниці між обсягом запасу на початку періоду і обсягом витраченого товару за час t: 
 за який відбувається повне вичерпання запасу знаходиться із рівняння
за який відбувається повне вичерпання запасу знаходиться із рівняння 
 , дорівнюють
, дорівнюють
 де коефіцієнт a визначає частку попиту b(t), який враховується. Тоді, оскільки дефіцит товару на момент часу t дорівнює величині z(t), то миттєві штрафні витрати за дефіцит у цей момент дорівнюють
де коефіцієнт a визначає частку попиту b(t), який враховується. Тоді, оскільки дефіцит товару на момент часу t дорівнює величині z(t), то миттєві штрафні витрати за дефіцит у цей момент дорівнюють  . Час
. Час  за який відбувається накопичення дефіциту до величини
за який відбувається накопичення дефіциту до величини  визначається із рівняння
визначається із рівняння  .
.
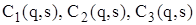 і рівність k(q) =Q/q, загальні витрати за період T дорівнюватимуть
і рівність k(q) =Q/q, загальні витрати за період T дорівнюватимуть
 (2.21)
(2.21)
 які доставляють мінімум функції
які доставляють мінімум функції 
 знаходимо, підставляючи в неї значення
знаходимо, підставляючи в неї значення  , одержуємо
, одержуємо  .
. на продукцію при відсутності запасу, є лінійною функцією часу і пропорційний функції споживання запасу при його наявності, тобто
на продукцію при відсутності запасу, є лінійною функцією часу і пропорційний функції споживання запасу при його наявності, тобто  де a
де a  – коефіцієнт пропорційності, який визначає кількість врахованих заявок на товар при його відсутності.
– коефіцієнт пропорційності, який визначає кількість врахованих заявок на товар при його відсутності.


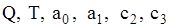

 ;
; в момент часу t;
в момент часу t; Розв’язання здійснюємо за оператором solve;
Розв’язання здійснюємо за оператором solve;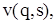 за який відбувається накопичення дефіциту до рівня q – s, розв’язуючи рівняння
за який відбувається накопичення дефіциту до рівня q – s, розв’язуючи рівняння 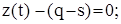
 і її частинні похідні
і її частинні похідні ,
,  ;
; при яких функція витрат
при яких функція витрат 
 .
.




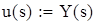
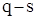







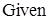





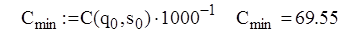 грош. од.
грош. од. одиниць, максимальний рівень запасу
одиниць, максимальний рівень запасу  одиниць, кількість замовлень
одиниць, кількість замовлень  . Пропорційно зменшенню частоти поставок
. Пропорційно зменшенню частоти поставок  у порівнянні з моделлю без дефіциту, зменшився інтервал часу між поставками, який дорівнює
у порівнянні з моделлю без дефіциту, зменшився інтервал часу між поставками, який дорівнює  доби. Мінімальне значення функції витрат дорівнює
доби. Мінімальне значення функції витрат дорівнює  грош. од. ▲
грош. од. ▲
 , пов’язані з дефіцитом запасу, включають постійну складову
, пов’язані з дефіцитом запасу, включають постійну складову 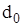 і складову
і складову  пропорційну тривалості дефіциту.
пропорційну тривалості дефіциту.


 .
. .
. ,
, . (2.22)
. (2.22) є функцією двох змінних q і s. Треба знайти абсолютний мінімум С(q, s) в області
є функцією двох змінних q і s. Треба знайти абсолютний мінімум С(q, s) в області  Оскільки функція С(q, s) диференційовна у всій області її визначення, то
Оскільки функція С(q, s) диференційовна у всій області її визначення, то  і
і  повинні задовольняти рівнянням
повинні задовольняти рівнянням


 .
. .
. .
. (2.23)
(2.23) і максимального рівня запасів
і максимального рівня запасів  для моделі з дефіцитом, втрати від якого пропорційні часу відсутності запасів
для моделі з дефіцитом, втрати від якого пропорційні часу відсутності запасів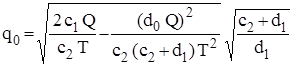 (2.24)
(2.24) (2.25)
(2.25) дорівнює розміру дефіциту. Коли коефіцієнт
дорівнює розміру дефіциту. Коли коефіцієнт  , формули (2.23) і (2.24) мають вигляд:
, формули (2.23) і (2.24) мають вигляд:

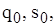 визначаємо інші параметри системи:
визначаємо інші параметри системи:
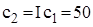 грош. од.; витрати у наслідок втрати замовлення без врахування втраченого прибутку
грош. од.; витрати у наслідок втрати замовлення без врахування втраченого прибутку  грош. од.; витрати, пропорційні тривалості дефіциту
грош. од.; витрати, пропорційні тривалості дефіциту  грош. од.; період роботи системи
грош. од.; період роботи системи  рік; час поставки поповнення запасу t = 9 місяців.
рік; час поставки поповнення запасу t = 9 місяців. оптимальний рівень запасів
оптимальний рівень запасів  кількість поставок
кількість поставок 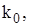 час між поставками
час між поставками  точку замовлення
точку замовлення  , виходячи із фіктивного рівня запасів, точку замовлення
, виходячи із фіктивного рівня запасів, точку замовлення 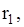 виходячи із рівня чистого запасу і обсяг дефіциту
виходячи із рівня чистого запасу і обсяг дефіциту  .
.






 і визначаємо величину
і визначаємо величину 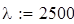




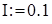



 грош. од.
грош. од.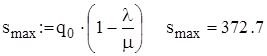

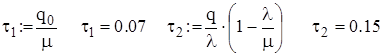






 од. Мінімальне значення функції витрат
од. Мінімальне значення функції витрат 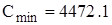 грош. од. У випадку необмеженої продуктивності, тобто при використанні формули Уілсона, він дорівнює
грош. од. У випадку необмеженої продуктивності, тобто при використанні формули Уілсона, він дорівнює  од., що на
од., що на 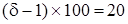 % менше, ніж у попередньому випадку. Максимальний наявний запас дорівнює
% менше, ніж у попередньому випадку. Максимальний наявний запас дорівнює  од., точка замовлення –
од., точка замовлення –  од. Відмітимо, що розмір замовлення
од. Відмітимо, що розмір замовлення  при необмеженій продуктивності. ▲
при необмеженій продуктивності. ▲ і поставок
і поставок  .
. повний цикл роботи системи;
повний цикл роботи системи; граничний запас на складі;
граничний запас на складі; вартість виготовлення виробу;
вартість виготовлення виробу; фіксовані витрати, пов’язані із запуском виробництва;
фіксовані витрати, пов’язані із запуском виробництва; коефіцієнт витрат зберігання запасу;
коефіцієнт витрат зберігання запасу; витрати на зберігання запасу;
витрати на зберігання запасу; втрати у наслідок не задовільнення замовлень клієнтів (дефіциту).
втрати у наслідок не задовільнення замовлень клієнтів (дефіциту). – період часу, коли у системі одночасно відбувається поповнення і витрачання запасу,
– період часу, коли у системі одночасно відбувається поповнення і витрачання запасу,  період часу, коли у системі відбувається витрачання створеного запасу,
період часу, коли у системі відбувається витрачання створеного запасу,  – період часу, коли у системі відбувається накопичення дефіциту запасу,
– період часу, коли у системі відбувається накопичення дефіциту запасу, 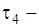 період часу, коли у системі відбувається компенсація дефіциту. При цьому у періоді
період часу, коли у системі відбувається компенсація дефіциту. При цьому у періоді  у системі є наявний запас, у періоді
у системі є наявний запас, у періоді 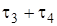 – запас відсутній.
– запас відсутній.
 (2.38)
(2.38) . (2.39)
. (2.39) через виражається через максимальний запас у вигляді
через виражається через максимальний запас у вигляді

 одержимо
одержимо


 одержимо витрати системи управління запасами в одиницю часу
одержимо витрати системи управління запасами в одиницю часу (2.40)
(2.40)
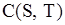 по
по  , і прирівнюючи їх нулю, одержимо систему рівнянь:
, і прирівнюючи їх нулю, одержимо систему рівнянь:

 ,
,  (2.41)
(2.41)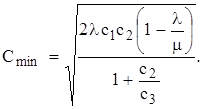 (2.42)
(2.42) . (2.43)
. (2.43) При цьому нестачі повністю виключаються
При цьому нестачі повністю виключаються  і
і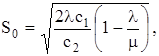


 (2.44)
(2.44)
 – умова, типова для поставок із складу, що стоїть вище, коли весь обсяг замовленої партії відвантажується разом. У цій моделі
– умова, типова для поставок із складу, що стоїть вище, коли весь обсяг замовленої партії відвантажується разом. У цій моделі




 (2.45)
(2.45)
 (2.46)
(2.46) і точка замовлення
і точка замовлення 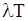 за період, так що для загального випадку
за період, так що для загального випадку


