
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Застосування подвійного інтеграла в геометрії
Площа плоскої фігури. На підставі властивостей подвійного інтеграла Для Отже, у прямокутних координатах
У полярній системі координат
Приклад 6.4. Обчислити площу фігури, що обмежена лініями Розв’язання. Розглянемо область Отже, Тоді
Приклад 6.5. Обчислити площу фігури, що обмежена лініями Розв’язання. Перетворимо перші два рівняння до канонічного вигляду, одержимо
Як видно з рисунка, дану площу не можна обчислити за допомогою одного подвійного інтеграла в прямокутних координатах. В полярній системі координат область є простою по Очевидно, що Тоді
Об'єм тіла. Виходячи з геометричного змісту подвійного інтеграла, об'єм тіла з основою
Приклад 6.6. Знайти об'єм тіла Розв’язання. Дане тіло є циліндричним з основою В силу симетричності тіла відносно координатної площини
Оскільки
Приклад 6.7. Обчислити об'єм тіла, обмеженого поверхнями
Розв’язання. Оскільки основою тіла в площині
де Отже Площа поверхні. Розглянемо поверхню, задану рівнянням
Застосування подвійного інтеграла у фізиці Маса плоскої пластини. Розглянемо тонку пластину, розташовану в площині, яка займає область Поверхневою щільністю такої пластинки в даній точці називається границя відношення маси
Якщо Нехай пластинка неоднорідна, тобто Розіб'ємо область Тоді масу кожної елементарної ділянки можна вважати приблизно рівною
Масу всієї пластинки
Точний результат знайдемо, перейшовши в останній рівності до границі:
Формулу (6.12) можна розглядати як механічний зміст подвійного інтеграла: подвійний інтеграл Статичні моменти. Аналогічно міркуючи, можна одержати формули для обчислення статичних моментів пластинки
Координати центра мас. У механіці доводиться, що статичний момент пластинки відносно якої-небудь осі збігається зі статичним моментом точкової маси, рівної масі пластинки, зосередженої в центрі ваги її відносно тієї ж осі. Звідси, позначаючи через
Отже,
Моменти інерції. Аналогічно, для моментів інерції пластинки одержуємо:
Можна показати, що полярний момент пластинки обчислюється за формулою
Очевидно, що
Приклад 6.8. Обчислити координати центра ваги півкола, щільність розподілу маси якого пропорційна квадрату відстані точки від діаметра цього півкола.
Розв’язання. Нехай вісь
|
||||||||||||||
|
Последнее изменение этой страницы: 2017-02-08; просмотров: 1120; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.151.106 (0.019 с.) |
 .
. підінтегральна функція
підінтегральна функція  і виходячи з геометричного змісту подвійного інтеграла одержимо об'єм циліндричного тіла висотою
і виходячи з геометричного змісту подвійного інтеграла одержимо об'єм циліндричного тіла висотою 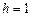 , що дорівнює площі основи тіла, тобто
, що дорівнює площі основи тіла, тобто 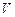 (од. куб.) =
(од. куб.) = 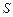 (од. кв.).
(од. кв.). . (6.9)
. (6.9) , тому
, тому . (6.10)
. (6.10) Рис. 6.11.
Рис. 6.11.
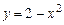 , y=x (рис. 6.11).
, y=x (рис. 6.11). і запишемо її нерівностями. Для цього знайдемо точки перетину ліній, що обмежують область (крайні точки області по вісі
і запишемо її нерівностями. Для цього знайдемо точки перетину ліній, що обмежують область (крайні точки області по вісі  ), розв’язавши систему рівнянь
), розв’язавши систему рівнянь 


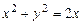 ,
,  ,
,  ,
,  .
. ,
,  . Перше рівняння визначає коло з центром у точці (1;0) з радіусом
. Перше рівняння визначає коло з центром у точці (1;0) з радіусом  , друге рівняння також визначає коло з центром у точці (2;0) з радіусом
, друге рівняння також визначає коло з центром у точці (2;0) з радіусом 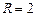 (рис. 6.12).
(рис. 6.12). Рис. 6.12.
Рис. 6.12.
 . Рівняння кіл, що обмежують область у полярній системі координат, одержимо, підставивши в їхні початкові рівняння
. Рівняння кіл, що обмежують область у полярній системі координат, одержимо, підставивши в їхні початкові рівняння  ,
,  . Тоді рівняння першого кола набуде вигляду
. Тоді рівняння першого кола набуде вигляду  , а для другого відповідно
, а для другого відповідно  .
.

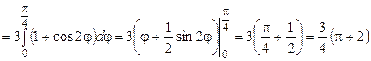 (кв. од.)
(кв. од.) , бічною поверхнею, паралельною вісі
, бічною поверхнею, паралельною вісі  , обмеженого зверху поверхнею заданою рівнянням
, обмеженого зверху поверхнею заданою рівнянням  , може бути обчислений за формулою
, може бути обчислений за формулою . (6.10)
. (6.10)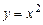 ,
,  ,
, 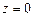 ,
,  (рис. 6.13).
(рис. 6.13).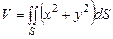 .
.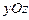 можна обчислити об'єм тіла з основою
можна обчислити об'єм тіла з основою  , (рис. 5.16), потім результат подвоїти.
, (рис. 5.16), потім результат подвоїти.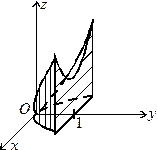




 ,
,  , z=0 (рис. 6.15).
, z=0 (рис. 6.15). Рис. 6.15.
Рис. 6.15.
 . Тому
. Тому 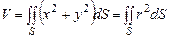 ,
,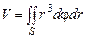 . Область
. Область 
 .
. . (6.11)
. (6.11)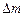 елементарної ділянки, що містить цю точку, до її площі
елементарної ділянки, що містить цю точку, до її площі  за умови, що площа ділянки стягується до даної точки. Позначимо щільність
за умови, що площа ділянки стягується до даної точки. Позначимо щільність  , маємо
, маємо .
. стала в кожній точці області, то маса обчислюється за формулою
стала в кожній точці області, то маса обчислюється за формулою  , де
, де  – площа пластинки.
– площа пластинки. .
.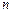 елементарних ділянок. У кожній ділянці розбивання довільно виберемо точу
елементарних ділянок. У кожній ділянці розбивання довільно виберемо точу  і будемо вважати, що щільність елементарної пластинки стала і така, як в обраній точці, тобто
і будемо вважати, що щільність елементарної пластинки стала і така, як в обраній точці, тобто  .
.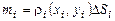 .
.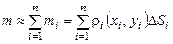 .
.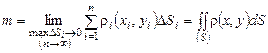 . (6.12)
. (6.12) дорівнює масі плоскої пластини, що займає область
дорівнює масі плоскої пластини, що займає область 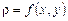 .
. ;
;  . (6.13)
. (6.13) координати центра мас пластинки
координати центра мас пластинки  ;
;  .
. ,
,  , (6.14)
, (6.14) ;
; 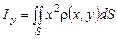 . (6.15)
. (6.15) . (6.16)
. (6.16) .
. Рис. 6.16.
Рис. 6.16.
 перпендикулярна до вісі
перпендикулярна до вісі  (рис. 6.16). При такому виборі осей координат щільність
(рис. 6.16). При такому виборі осей координат щільність  (
( – коефіцієнт пропорційності),
– коефіцієнт пропорційності),  ,
,  , де
, де  ,
, ,
, .
.


