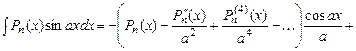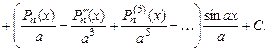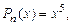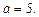Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Заміна змінної при інтегруванні.Стр 1 из 12Следующая ⇒
Нехай на деякому проміжку визначена складна функція
Формулу (5.3) називають формулою заміни змінної при інтегруванні. Приклад 5.10. Обчислити інтеграл Розв’язання.
Вибір конкретної заміни “підказується” властивістю інтегралу. Приклад 5.11. Обчислити інтеграл Розв’язання.
Приклад 5.12. Обчислити інтеграл Розв’язання. Розділивши чисельник та знаменник функції на Ці перетворення підказують наступну заміну:
Приклад 5.13. Обчислимо інтеграл Розв’язання. Застосуємо підстановку Тоді і З рівності Приклад 5.14. Обчислити інтеграл Розв’язання. Обчислимо даний інтеграл кількома способами. а) Нехай
б) Нехай
в) Покладемо Помітимо, що якщо первісна
Інтегрування частинами у невизначеному інтегралі. Цей метод опирається на рівність
яку називають формулою інтегрування частинами. Застосування формули (5.4) доцільно у тих випадках, коли підінтегральний вираз По відомому диференціалу Іноді для обчислення інтегралу формулу інтегрування по частинам доводиться застосовувати декілька разів. Приклад 5.15. Обчислити інтеграл Розв’язання.
Приклад 5.16. Обчислити інтеграл
Розв’язання.
Обчислимо інтеграл:
Остаточно маємо Приклад 5.17. Обчислити інтеграл Розв’язання.
Таким чином
Приклад 5.18. Обчислити інтеграл Розв’язання.
Таким чином
Приклад 5.19. Обчислити інтеграл Розв’язання. Шляхом інтегрування частинами
По формулі (5.5) Приклад 5.20. Обчислити інтеграл Розв’язання. В цьому випадку прийшлося б п’ять разів інтегрувати по частинам, кожного разу вибираючи многочлен за
В нашому випадку
|
|||||
|
Последнее изменение этой страницы: 2017-02-08; просмотров: 268; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.45.137 (0.015 с.) |
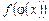 і функція
і функція 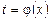 неперервна на цьому проміжку. Тоді:
неперервна на цьому проміжку. Тоді: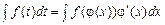 . (5.3)
. (5.3)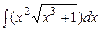 .
.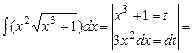
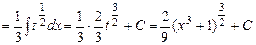 .
.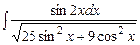 .
.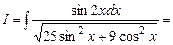
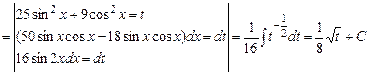 , або, повертаючись до змінної
, або, повертаючись до змінної  , маємо
, маємо 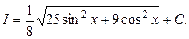
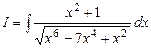 .
.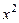 , маємо
, маємо 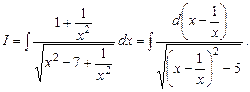
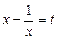 . Тоді:
. Тоді: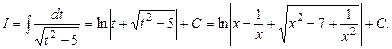
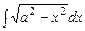 ,
, 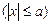 .
.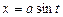 ,
, 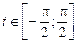 .
.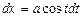 ,
,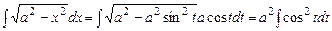 (зауважимо, що оскільки
(зауважимо, що оскільки 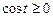 для
для  дорівнює
дорівнює 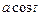 ); беручи інтеграл, одержуємо
); беручи інтеграл, одержуємо 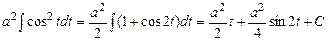 .
.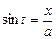 одержимо, що
одержимо, що  ,
, 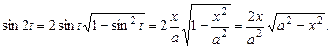 Остаточно маємо
Остаточно маємо 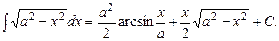 Значення цього інтегралу наведено в таблиці основних інтегралів.
Значення цього інтегралу наведено в таблиці основних інтегралів.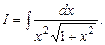
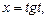
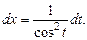 Маємо
Маємо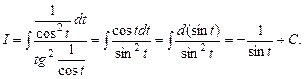 Враховуючи, що
Враховуючи, що 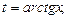 а
а 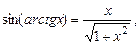 одержуємо
одержуємо 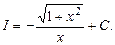
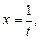
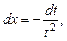 отже,
отже,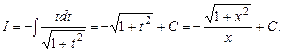
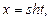 тоді
тоді 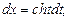 причому
причому 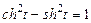 маємо
маємо 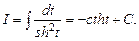 Враховуючи, що
Враховуючи, що 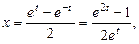 розв’язуючи рівняння
розв’язуючи рівняння 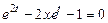 відносно
відносно  - параметр) та відкинувши
- параметр) та відкинувши 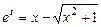 ,
, 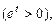 маємо
маємо 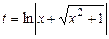 . Формально одержимо іншу відповідь порівняно з рішенням у пп. “а”, “б”, але можна одержати ту ж саму відповідь, якщо враховувати, що
. Формально одержимо іншу відповідь порівняно з рішенням у пп. “а”, “б”, але можна одержати ту ж саму відповідь, якщо враховувати, що 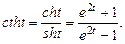
 існує, то при різних підстановках відрізняється лише сталою. Цей інтеграл можна обчислити за допомогою інших підстановок (
існує, то при різних підстановках відрізняється лише сталою. Цей інтеграл можна обчислити за допомогою інших підстановок (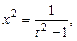
 ). Це свідчить про творчий процес інтегрування.
). Це свідчить про творчий процес інтегрування. (5.4)
(5.4)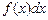 вдається представити у вигляді добутку двох множників
вдається представити у вигляді добутку двох множників  і
і 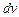 таким чином, щоб інтегрування виразів
таким чином, щоб інтегрування виразів 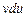 стало задачею більш простою, ніж інтегрування початкового виразу.
стало задачею більш простою, ніж інтегрування початкового виразу. визначається неоднозначною, але у формулі (5.4) за
визначається неоднозначною, але у формулі (5.4) за 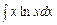 .
.
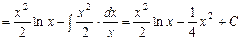 .
. .
.
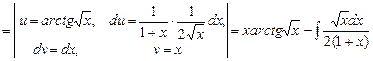 .
.
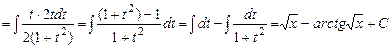 .
.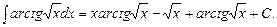
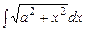 .
.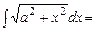
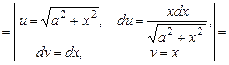
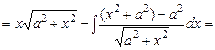
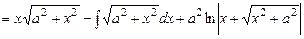 .
.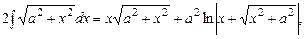
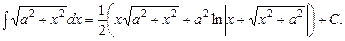
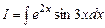 .
.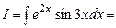
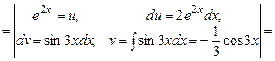
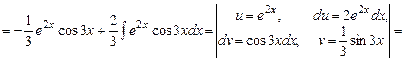
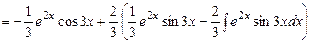 .
.
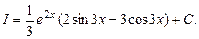
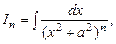
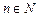 .
.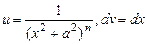 можна одержати рекурентну формулу для обчислення інтегралу:
можна одержати рекурентну формулу для обчислення інтегралу: 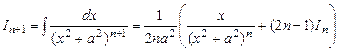 (5.5)
(5.5)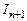 зводиться до
зводиться до 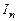 (будемо писати
(будемо писати 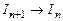 ),
), 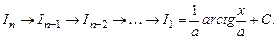
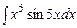 .
.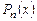 – многочлен)
– многочлен)