
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
V. Точность измерительных приборов.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Точность измерительного прибора – это его свойство, характеризующее степень приближения показаний данного измерительного прибора к действительным значениям измеряемой величины и определяется той наименьшей величиной, которую с помощью этого прибора можно определить надёжно. Точность прибора зависит от цены наименьшего деления его шкалы и указывается или на самом приборе, или в заводской инструкции (паспорте). Заметим, что точность измерений Погрешность электроизмерительных приборов определяется классом точности (или приведенной погрешностью Епр), который указывается на лицевой стороне прибора соответствующей цифрой в кружке. Классом точности прибора К называют выраженное в процентах отношение абсолютной погрешности
Зная класс точности и предел измерения прибора, можно рассчитать его абсолютную погрешность:
Эта погрешность одинакова для любого измерения сделанного с помощью данного прибора. Классов точности семь: 0,1; 0,2; 0,5; 1,0; 1,5; 2,5; 4,0. Приборы первых трех классов точности (0,1; 0,2; 0,5) называются прецизионными и используются при точных научных измерениях, приборы остальных классов точности называются техническими. Приборы без указания класса точности считаются внеклассными. Пример. Сила тока измеряется в цепи амперметром, класс точности которого К=0,5, а шкала имеет предел измерения Iпр=10 А. Находим абсолютную погрешность амперметра:
Отсюда следует, что амперметр позволяет измерять силу тока с точностью не более 0,05 А, и поэтому нецелесообразно делать отсчёт по шкале прибора с большей точностью. Допустим, что с помощью данного амперметра были измерены три значения силы тока: I1=2 А; I2=5 А; I3=8 А. Находим для каждого случая относительную погрешность: Из этого примера следует, что в третьем случае относительная погрешность самая маленькая, то есть чем больше величина отсчёта по прибору, тем меньше относительная погрешность измерения. Вот почему для оптимального использования приборов рекомендуется их подбирать так, чтобы значение измеряемой величины находилось в конце шкалы прибора. В этом случае относительная погрешность приближается к классу точности прибора. Если точность прибора неизвестна, то абсолютная погрешность принимается равной половине цены наименьшего деления (линейка, термометр, секундомер). Для штангенциркуля и микрометра – точность их нониусов (0,1 мм, 0,01 мм). Примечания: 1) При отсчетах следует следить за тем, чтобы луч зрения был перпендикулярен шкале. Для устранения так называемой ошибки параллакса на многих приборах устанавливается зеркало («зеркальные приборы»). Глаз экспериментатора расположен правильно, если стрелка прибора закрывает свое изображение в зеркале. 2) При косвенных измерениях (например, определение объема цилиндра по его диаметру и высоте) следует определять все измеряемые вершины с приблизительно одинаковой относительной точностью. 3) При обработке результатов измерений следует помнить, что точность вычислений должна быть согласована с точностью самих измерений. Вычисления, произведенные с большим, чем это необходимо, числом десятичных знаков, приводят к большому объему ненужной работы. Например, если хотя бы одна из величин в каком-либо выражении определена с точностью до двух значащих цифр, то нет смысла вычислять результат с точностью, большей двух значащих цифр. В тоже время в промежуточных расчетах рекомендуется сохранять одну лишнюю цифру, которая в дальнейшем – при записи окончательного результата – будет отброшена. В теории погрешностей из существующих правил округления имеется следующее исключение: при округлении погрешностей последняя сохраняемая цифра увеличивается на единицу, если старшая отбрасываемая цифра 3 или больше 3. 4) Примеры окончательной записи результатов измерений: Правильно Неправильно 84 ± 1 84,5 ± 1 2780 ± 14 2782 ± 14 350 ± 38 352 ± 38 52,7 ± 0,3 52,72 ± 0,3 13,840 ± 0,013 13,8362 ± 0,013 4,750 ± 0,006 4,75 ± 0,006 5390 ± 28 5391 ± 28
|
||||
|
Последнее изменение этой страницы: 2017-02-05; просмотров: 4602; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.15.18 (0.006 с.) |

 обратно пропорциональна относительной погрешности измерений Е:
обратно пропорциональна относительной погрешности измерений Е:  .
. к предельному (номинальному) значению хпр измеряемой величины, т. е. к наибольшему её значению, которое может быть измерено по шкале прибора (предел измерения):
к предельному (номинальному) значению хпр измеряемой величины, т. е. к наибольшему её значению, которое может быть измерено по шкале прибора (предел измерения): .
. .
.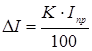
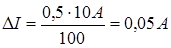
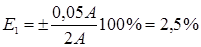 ;
; 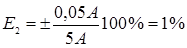
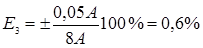 .
.


