
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Решение задачи в процедуре EXCEL
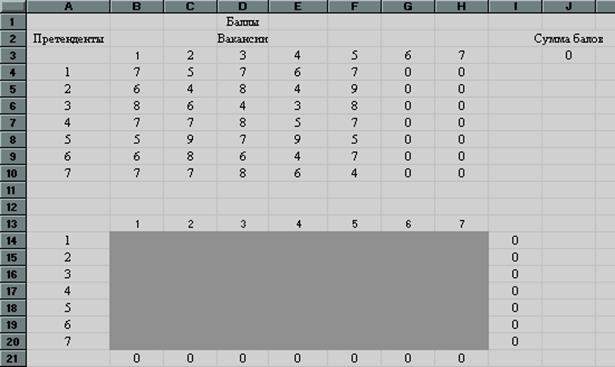
«Поиск решения» 1) Ввод данных. Переносим данные задачи в EXCEL, при этом нужно ввести 2 столбца (6-ой и 7-ой) с нулевыми значениями для сбалансирования задачи. Результаты заполнения таблицы EXCEL можно увидеть на рис.24:
Рис.24 В ячейках B4: F10 введены результаты тестирования претендентов, а в ячейках G4: H10 введены нули, что соответствует фиктивным вакансиям. Ячейки B14: F20 являются изменяемыми ячейками для нашей процедуры. В ячейках B21: H21 находятся суммы значений соответствующих столбцов изменяемых ячеек. Так в ячейке B21 находится сумма ячеек B14: B20. Аналогично в ячейках: в С21 находится сумма ячеек С14: С20; в D21 находится сумма ячеек D14: D20; в E21 находится сумма ячеек E14: E20; в F21 находится сумма ячеек F14: F20. в G21 находится сумма ячеек G14: G20; в H21 находится сумма ячеек H14: H20. В ячейках I14: I20 находятся суммы значений соответствующих строк изменяемых ячеек. Так в ячейке I14 находится сумма ячеек B14: H14. Аналогично в ячейках: в I15 находится сумма ячеек B15: H15; в I16 находится сумма ячеек B16: H16; в I17 находится сумма ячеек B17: H17; в I18 находится сумма ячеек B18: H18; в I19 находится сумма ячеек B19: H19; в I20 находится сумма ячеек B20: H20. Целевая функция заносится в ячейку J3 и вычисляется по формуле «СУММПРОИЗВ(B4:H10;B14:H20)».
3) Заполнение окна процедуры «Поиск решения»:
целевая функция: J3; значение целевой функции: max; изменяемые ячейки: B14: H20; ограничения задачи: B21: H21 =1 и I14: I20 = 1(все свободные рабочие места должны быть заняты); B14: F20 В окне «Параметры» установить «Линейная модель», что соответствует решению задачи симплекс-методом. Результаты заполнения окна показаны на рис.25:
Рис.25
3) Выполнив процедуру «Поиск решения» мы получили в первоначальной таблице следующие результаты (таблица 26):
Рис.26 Эти результаты совпадают с решением задачи, полученным преобразованием матрицы (С).
Задача коммивояжера
В 1859 г. У. Гамильтон придумал игру «Кругосветное путешествие», состоящую в отыскании такого пути, проходящего через все вершины (города, пункты назначения) графа, чтобы посетить каждую вершину однократно и возвратиться в исходную. Пути, обладающие таким свойством, называются гамильтоновыми циклами.
Задача о гамильтоновых циклах в графе получила различные обобщения. Одно из этих обобщений – задача коммивояжера, Особенностью задачи о коммивояжере является необходимость дополнительно учитывать расстояния от города до города, которые предполагаются известными. Эти «расстояния» можно заменить на количество затраченного времени, стоимость проезда или предполагать другие произвольные значения. В общем случае мы даже не предполагаем, что стоимость проезда из I в J обязательно совпадает со стоимостью обратного проезда из I в J. Примером реализации задачи на практике является составление оптимального маршрута человека для доставки продуктов в магазины с оптового склада; доставки бутилированной воды; обновления программных продуктов автоматизированного учета на предприятии; пополнения банкоматов наличными деньгами; сбора сотрудников для доставки вахтовым методом; расклейки афиш; сбора наличных денежных средств их терминалов и др. В этом случае вершинами являются места установки терминалов (банкоматов и т.д.) и «базовый пункт». Стоимостью каждого ребра (отрезка маршрута) является время в пути между двумя точками (вершинами) на маршруте. Сверлильный станок изготавливает металлические листы с некоторым количеством отверстий. Координаты отверстий известны. Необходимо найти кратчайший путь через все отверстия, а значит, и наименьшее время, затрачиваемое на изготовление одной детали. В данном случае, если такой станок делает миллион деталей в год, то даже миллиметровая выгода может сэкономить приличные средства.
Решение задачи коммивояжера при помощи надстройки MS Excel «Поиск решения »
Мощным средством анализа данных MS Excel является надстройка «Поиск решения». С ее помощью можно определить, при каких значениях указанных влияющих ячеек формула в целевой ячейке принимает нужное значение (минимальное, максимальное или равное какой-либо величине). Для процедуры поиска решения можно задать ограничения, причем не обязательно, чтобы при этом использовались те же влияющие ячейки, данные которых, определяют значение целевой ячейки. Для расчета заданного значения применяются различные математические методы поиска. Вы можете установить режим, в котором полученные значения переменных автоматически заносятся в таблицу. Кроме того, результаты работы программы могут быть оформлены в виде отчета.
Программа Поиск решений – дополнительная надстройка табличного процессора MS Excel, которая предназначена для решения определенных систем уравнений, линейных и нелинейных задач оптимизации, используется с 1991 года. Размер задачи, которую можно решить с помощью базовой версии этой программы, ограничивается такими предельными показателями: количество неизвестных (decision variable) – 200; количество формульных ограничений (explicit constraint) на неизвестные – 100; количество предельных условий (simple constraint) на неизвестные – 400. Постановка задачи коммивояжера, которую необходимо решить посредством надстройки «Поиск решения» методом полного перебора следующая: Требуется побывать в пяти организациях: А, Б, В, Г и Д., начиная с организации А и, вернутся в пункт А. В каком порядке следует обходить организации, чтобы замкнутый тур был кратчайшим? Расстояния между каждой парой организаций заданы следующей матрицей
Решение: Разместим исходные данные на рабочем листе (рис 2.1). Заменим знак
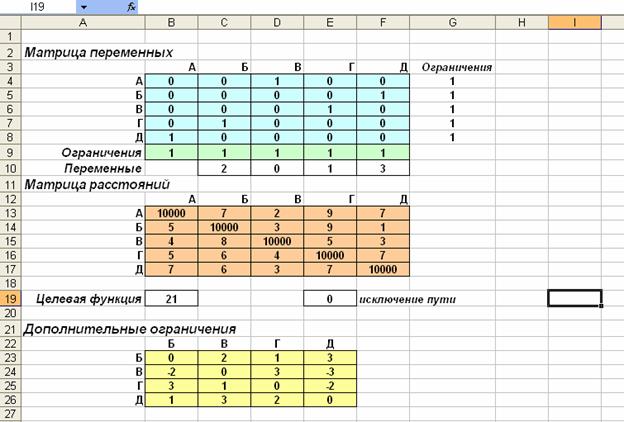
Рисунок 2.1 Исходные данные задачи
Вводим формулы:
Таблица 1
Сценарий решения. 2. Для того чтобы выполнялись условия однократного посещения сотрудником организаций и в то же время запланированный Петровым маршрут был пройден полностью, введем ограничения: в строки B9, G4 заводим формулы из таблицы 1 и распространяем их на соответствующие диапазоны B9:F9 и G4:G8. Задаем следующие данные $B$9:$F$9=1 и $G$4:$G$8=1 в Ограничения окна «Поиск решения». Таким образом, мы можем отследить порядок обхода организаций сотрудником, оценить правильность выбора и оптимальность его маршрута. 3. Выбираем ячейку B19 и устанавливаем ее адрес в Целевую ячейку окна «Поиск решения», чтобы определить длину наикратчайшего маршрута. Для этого в ячейку B19 предварительно заносим соответствующую формулу из таблицы 1. Когда программа «Поиск решения» вычислит оптимальный маршрут Петрова и станет известен порядок обхода организаций (из Матрицы переменных) будут известны и расстояния между конкретными парами организаций. Затем при помощи простых математических подсчетов программа рассчитает протяженность оптимального маршрута.
4. Устанавливаем еще одно ограничение в окно «Поиск решения»: $E$19=0. В указанную ячейку вводим формулу из таблицы 1 и исключаем таким образом, заведомо ложный порядок движения Петрова в порядке обхода организаций.
5. В связи с тем, что ячейки диапазона B4:F8 – изменяемые, в Ограничение окна «Поиск решения» необходимо добавить строку B$4$:F$8$=двоичное.
6. Заводим в ячейки B23; B24; B25; B26 соответствующие формулы из таблицы 1 и распространяем их на следующие диапазоны: B23:E23 B24:E24; B25:E25; B26:E26 для учета всех возможных вариантов обхода организаций сотрудником и выбора из них оптимального. Формулы задаем таким образом, чтобы обеспечить исключение ложного пути, соблюдая условие задачи об обходе всех организаций по одному разу.
7. Добавляем в Ограничения окна «Поиск решения» $B$23:$E$26 ≤ 3.
Рисунок 2.2 Окно «Поиск решения»
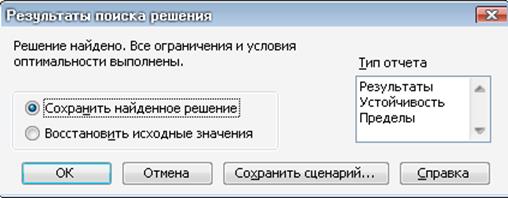
В окне «Параметры поиска решений» отметить Линейная модель и Неотрицательные значения (рис. 2.3) «OK»
Рисунок 2.3 Окно «Параметры поиска решения»
«Сохранить найденное решение» и ОК.
Найденная минимальная величина находится в целевой ячейке, а в переменных ячейках - оптимальные значения переменных, В диапазоне B4:F8 отражается порядок перемещений. Если в ячейке, В стоит единица, значит сотрудник посетил эту организацию следующей за А. Если в ячейке ноль – сотрудник организацию не посещал.
Рисунок 2.4 Результаты решения задачи коммивояжера Экономико-математическая модель межотраслевого баланса (модель Леонтьева). Рассмотрим модель межотраслевого баланса, называемую еще моделью Леонтьева или моделью «затраты-выпуск». Предположим, что производственный сектор народного хозяйства разбит на n отраслей (энергетика, машиностроение, сельское хозяйство и т.д.). Рассмотрим отрасль i, i = 1, 2,…, n. Она выпускает некую продукцию за данный промежуток времени (например, за год) в объеме xi, который еще называют валовым выпуском. Часть объема продукции xi, произведенная i-ой отраслью используется для собственного производства в объеме xii, часть – поступает в остальные отрасли j = 1, 2,…, n для потребления при производстве в объемах xij, и некоторая часть объемом yi – для потребления в непроизводственной сфере, так называемый объем конечного потребления. Перечисленные сферы распределения валового продукта i-ой отрасли приводят к соотношению баланса Введем коэффициенты прямых затрат a ij, которые показывают, сколько единиц продукции i-ой отрасли затрачивается на производство одной единицы продукции в отрасли j. Тогда можно записать, что количество продукции, произведенной в отрасли i в объеме xij и поступающей для производственных нужд в отрасль j, равно Считаем сложившуюся технологию производства во всех отраслях неизменной (за рассматриваемый период времени), означающую, что коэффициенты прямых затрат a ij постоянны. Тогда получаем следующее соотношение баланса, называемого моделью Леонтьева
Введя вектор валового выпуска X, матрицу прямых затрат A и вектор конечного потребления Y модель Леонтьева (1) можно записать в матричном виде X = AX + Y (2) Матрица A ≥ 0, у которой все элементы a ij ≥ 0 (неотрицательны), называется продуктивной матрицей, если существует такой неотрицательный вектор X ≥ 0, для которого выполняется неравенство X > AX. Это неравенство означает, что существует хотя бы один режим работы отраслей данной экономической системы, при котором продукции выпускается больше, чем затрачивается на ее производство. Другими словами, при этом режиме создается конечный (прибавочный) продукт Y = X – AX > 0. Модель Леонтьева с продуктивной матрицей A называется продуктивной моделью. Существует несколько критериев продуктивности матрицы A. Один из них говорит о том, что матрица A продуктивна, если максимум сумм элементов ее столбцов не превосходит единицы, причем хотя бы для одного из столбцов сумма элементов строго меньше единицы. Для проверки продуктивности матрицы A также достаточно существования обратной матрицы B = (E – A)-1 с неотрицательными элементами, где матрица E – единичная матрица С помощью модели Леонтьева (2) можно выполнить три вида плановых расчетов, при условии соблюдения условия продуктивности матрицы A: 1) Зная (или задавая) объемы валовой продукции всех отраслей X можно определить объемы конечной продукции всех отраслей Y Y = (E – A)X 2) Задавая величины конечной продукции всех отраслей Y можно определить величины валовой продукции каждой отрасли X = (E – A)-1Y (3) 3) Задавая для ряда отраслей величины валовой продукции, а для всех остальных отраслей – объемы конечной продукции, можно найти величины конечной продукции первых отраслей и объемы валовой продукции вторых. Матрица B = (E – A)-1 называется матрицей полных материальных затрат. Ее смысл следует из матричного равенства (3), которое можно записать в виде X = BY. Элементы матрицы B показывают, сколько всего необходимо произвести продукции в i-ой отрасли, для выпуска в сферу конечного потребления единицы продукции отрасли j. Пример 1. Объемы промежуточной продукции в линейной статической модели Леонтьева представлены матрицей Решение: Пример 2. Матрица коэффициентов прямых затрат линейной статической модели Леонтьева имеет вид Решение:
В линейной статической модели Леонтьева объемы конечного продукта представлены вектором
Решение: Пример 4. Статическая линейная модель межотраслевого баланса Леонтьева представлена системой уравнений: Решение: Пример 5. Статическая линейная модель Леонтьева многоотраслевой экономики продуктивна. Укажите номер ячейки, где записана матрица коэффициентов прямых затрат:
Решение:
Пример 6. Укажите номер ячейки, где записана матрица коэффициентов прямых затрат статической линейной модели Леонтьева:
Решение: Пример 7. Матрица коэффициентов прямых затрат линейной статической модели Леонтьева имеет вид Решение: Статическая линейная модель межотраслевого баланса Леонтьева в матричной форме моделируется системой
Пример 8. В линейной статической модели Леонтьева объемы конечного продукта представлены вектором Решение:
Пример 9. В таблице приведены данные об исполнении баланса за отчетный период в усл. ден. ед.:
Требуется найти объем валового выпуска каждого вида продукции, если конечное потребление по отраслям увеличить соответственно до 60, 70 и 30 условных денежных единиц. Решение. Выпишем векторы валового выпуска и конечного потребления и матрицу коэффициентов прямых затрат
По формуле
Запишем матрицу прямых затрат:
Она является неотрицательной и удовлетворяет критерию продуктивности: max{0,05 + 0,1+02=0,35; 0,35 + 0,1+0,1=0,55; 0,04+0,4+0,2=0,64}=max{0,35; 0,55; 0,64} = 0,64 < 1. Поэтому для любого вектора конечного продукта Y можно найти необходимый объем валового выпуска X по формуле X=(E–A)-1Y. Определим матрицу полных затрат S=(E–A)-1:
Так как |E−A|=0,5824, то
По условию новый вектор конечного продукта
Тогда по формуле X=(E–A)-1Y получаем новый вектор валового выпуска:
Вычислим, на сколько процентов новые значения компонент вектора
и выразим эти значения в процентах от исходных компонент:
Таким образом, для того чтобы обеспечить заданное увеличение компонент вектора конечного продукта Y, необходимо увеличить валовые выпуски (компоненты вектора X) в следующих пропорциях: добычу и переработку углеводородов на 13,26%, уровень энергетики — на 26,65% и выпуск продукции машиностроения — на 26,52% по сравнению с отчетным периодом. Решение задачи межотраслевого баланса (модель Леонтьева)средствами Excel. Задача. Экономическая система состоит из трех отраслей, для которых матрица прямых затрат A и вектор конечного продукта Y известны: Определить: 1) Матрицу коэффициентов полных материальных затрат B 2) Проверить продуктивность матрицы A 2) Вектор валового выпуска X 3) Межотраслевые поставки продукции xij
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-05; просмотров: 851; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.216.251.37 (0.088 с.) |
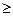 0 (изменяемые ячейки должны иметь положительные значения).
0 (изменяемые ячейки должны иметь положительные значения).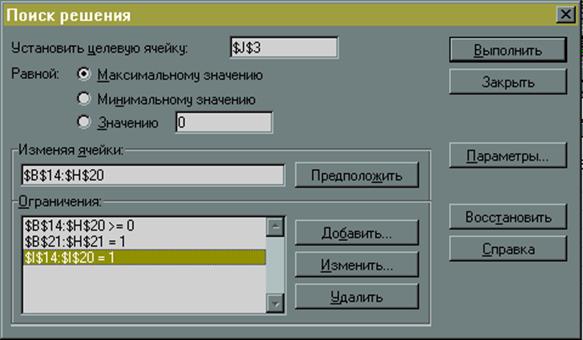
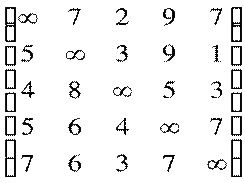
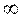 числом 10000 (на результат решения не влияет)
числом 10000 (на результат решения не влияет)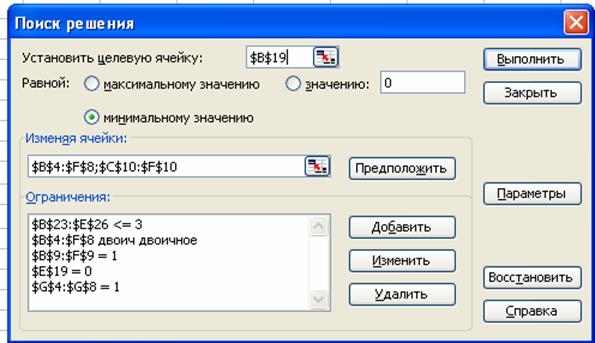
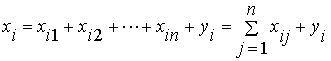 , i = 1, 2,…, n.
, i = 1, 2,…, n.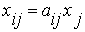
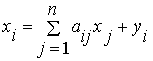 , i = 1, 2,…, n. (1)
, i = 1, 2,…, n. (1)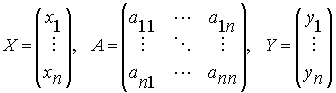
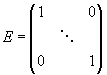 .
.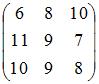 , а объемы валовых выпусков – вектором
, а объемы валовых выпусков – вектором  . Найти объемы конечного продукта.
. Найти объемы конечного продукта.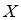 , конечный продукт
, конечный продукт 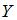 и промежуточное потребление
и промежуточное потребление 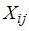 связаны системой уравнений:
связаны системой уравнений: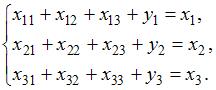
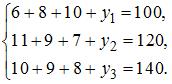
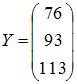 .
.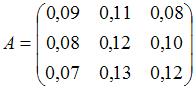 , а объемы валовых выпусков представлены вектором
, а объемы валовых выпусков представлены вектором 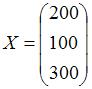 . Найти объемы промежуточной продукции.
. Найти объемы промежуточной продукции.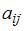 вычисляются по формуле
вычисляются по формуле 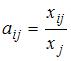 , где
, где 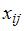 – объем промежуточной продукции
– объем промежуточной продукции 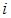 -ой отрасли, который используется в
-ой отрасли, который используется в 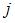 -ой отрасли,
-ой отрасли, 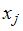 – объем валового выпуска в
– объем валового выпуска в 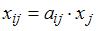 , то есть
, то есть 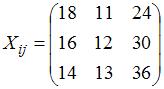 .
. , объемы валовых выпусков – вектором
, объемы валовых выпусков – вектором  . Тогда объемы промежуточной продукции можно представить матрицей …
. Тогда объемы промежуточной продукции можно представить матрицей …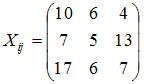
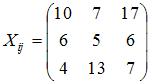
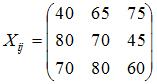
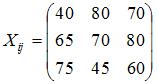
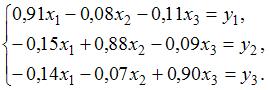
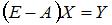 , где
, где 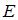 – единичная матрица. Тогда матрица
– единичная матрица. Тогда матрица 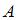 коэффициентов прямых затрат будет равна:
коэффициентов прямых затрат будет равна: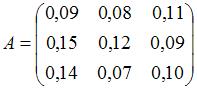 .
.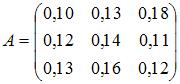 ;
;
 ;
;
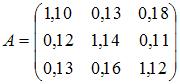 ;
;
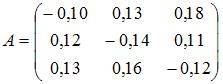
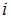 -ой отрасли, который используется в
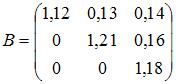
-ой отрасли, который используется в 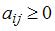 . Во-вторых, модель Леонтьева продуктивна, если сумма элементов каждой строки матрицы не больше единицы и хотя бы для одной строки эта сумма меньше единицы. Обоим этим условиям удовлетворяет матрица
. Во-вторых, модель Леонтьева продуктивна, если сумма элементов каждой строки матрицы не больше единицы и хотя бы для одной строки эта сумма меньше единицы. Обоим этим условиям удовлетворяет матрица 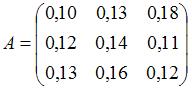
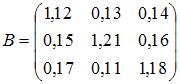 ;
;
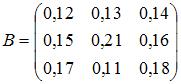 ;
;
 ;
;
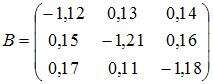
 показывают, на сколько единиц увеличится валовой выпуск
показывают, на сколько единиц увеличится валовой выпуск 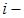 ой отрасли при увеличении конечного выпуска в
ой отрасли при увеличении конечного выпуска в 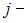 ой отрасли на одну единицу. Поэтому
ой отрасли на одну единицу. Поэтому 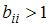 , а
, а 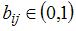 , при
, при 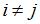 . Этим условиям удовлетворяет матрица
. Этим условиям удовлетворяет матрица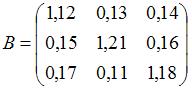 .
.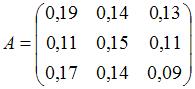 . Запишите систему уравнений модели межотраслевого баланса
. Запишите систему уравнений модели межотраслевого баланса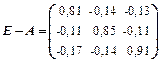 , тогда система уравнений модели межотраслевого баланса выглядит следующим образом:
, тогда система уравнений модели межотраслевого баланса выглядит следующим образом: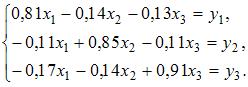
 , матрица коэффициентов полных затрат имеет вид
, матрица коэффициентов полных затрат имеет вид  . Найти объемы валовых выпусков.
. Найти объемы валовых выпусков.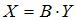 , где
, где 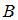 – матрица коэффициентов полных затрат, а
– матрица коэффициентов полных затрат, а 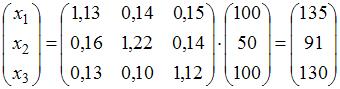
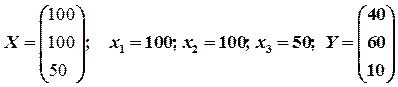
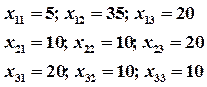
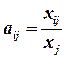 вычислим коэффициенты прямых затрат:
вычислим коэффициенты прямых затрат: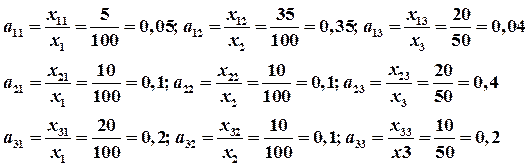
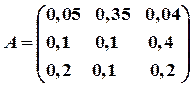
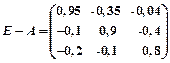
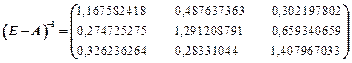
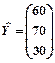
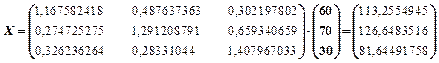
 валового продукта больше, чем для исходного
валового продукта больше, чем для исходного  . Найдем приращения компонент:
. Найдем приращения компонент: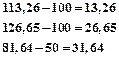
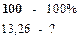
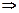
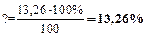
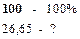
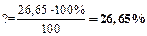
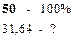
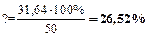
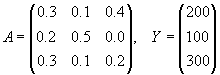 .
.


