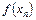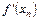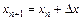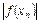Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема 2. Розв’язання трансцендентних рівнянь з одним невідомим
Завдання 2. Для заданого трансцендентногорівняння відокремити корені і знайти їх з точністю 1) методом половинного поділу (дихотомії), 2) методом дотичних (Н’ютона), 3) методом простих ітерацій. Варіанти виконання завдання 2
Розв’язання рівняння методом дихотомії Порядок виконання.
Для заданого нелінійного рівняння 1) Представити рівняння у вигляді 2) Нарисувати на одному рисунку графіки функцій 3) Провести аналітичну перевірку відокремлення коренів для кореня, найменшого по абсолютній величині (на рисунку - найбільш близький до початку координат). 4) Уточнити цей корінь із заданою точністю Приклад розв'язання рівняння
1) Легко перевірити, що 2) Побудуємо на одному рисунку графіки функцій 3) Проведемо аналітичну перевірку відокремлення цього кореня. Функція
Отже на інтервалі
Знайшовши значення похідної в проміжних точках інтервалу
Уточнюємо методом дихотомії корінь, що належить інтервалу
Таблиця 2 - Розрахункова таблиця знаходження кореня рівняння
Моментом зупинки обчислень є виконання у поточному рядку таблиці 1 умови | b-a | < ε, тобто визначаємо його по останньому стовпцю таблиці (коли значення в цьому стовпці стає менше від Розв"язання рівняння методом дотичних Порядок виконання.
Для заданого рівняння 1) Виконати пункти 1-3, що зазначені у попередньому методі 2) Знайти другу 3) Перевірити, чи зберігає знак 4) Уточнити цей корінь із заданою точністю Теоретичні відомості. Стартове значення ітераційної змінної хn: Ітераційна схема методу дотичних має вигляд: Момент зупинки. Моментом зупинки обчислень вибираємо умову Таблиця 3 - Розрахункова таблиця знаходження кореня рівняння
Рядки таблиці заповнюються зліва направо. Зупинка обчислень ведеться по значенню в графі 7. Воно повинно стати меншим ніж δ=ε∙m1.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-07; просмотров: 129; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.6.77 (0.007 с.) |
 *:
*:
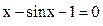
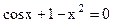
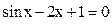



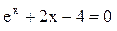
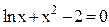
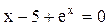
 :
: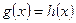 , для якого легко побудувати графіки функцій
, для якого легко побудувати графіки функцій 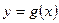 і
і 
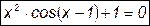 методом дихотомії.
методом дихотомії.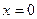 не є коренем рівняння. Представимо рівняння
не є коренем рівняння. Представимо рівняння  у вигляді
у вигляді 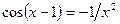 .
.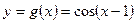 і
і  . З рисунка бачимо, що є нескінченно багато точок перетину графіків цих функцій, а найменший корінь за абсолютною величиною знаходиться в інтервалі
. З рисунка бачимо, що є нескінченно багато точок перетину графіків цих функцій, а найменший корінь за абсолютною величиною знаходиться в інтервалі 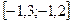 , і він в цьому інтервалі один.
, і він в цьому інтервалі один.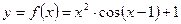 неперервна на інтервалі
неперервна на інтервалі 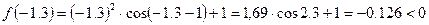 ,
,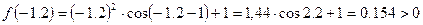 .
. на кінцях інтервала дорівнює
на кінцях інтервала дорівнює 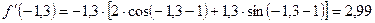 ,
,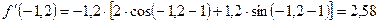 .
. ,
,  ). Це означає, що на інтервалі
). Це означає, що на інтервалі 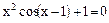 методом дихотомії
методом дихотомії
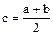
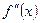 похідну функції
похідну функції 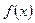 .
. .
.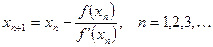 .
. , де
, де 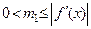 на [ а,b ]. Обчислення зручно звести у таблицю 3 із шапкою виду:
на [ а,b ]. Обчислення зручно звести у таблицю 3 із шапкою виду: