
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Степенная функция во множестве действительных чисел
Пусть m - произвольное вещественное число. Определим общую степенную функцию Из определения степенной функции следует, что при m > 0 она представляет собой возрастающую, а при m < 0 убывающую функцию. Рассмотрим предельное значение степенной функции при
Действительно, пусть
Степенно-показательная функция Определение №1. Функция вида Примеры: 1. Если
2. Тогда 3. Отсюда следует, что в силу непрерывности логарифмической и показательной функций, функция
4. Представление степенно-показательной функции в виде 5. Значит, если существуют пределы 6. Если
Некоторые пределы, связанные с показательными и Логарифмическими функциями Известны формулы первого и второго замечательных пределов и следствия к ним. 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. Докажем, что Доказательство: 1. Запишем 2. Возведем обе части равенства в степень 3. Тогда предел примет вид:
= 3. Обратные тригонометрические функции I. 1. Рассмотрим функцию 2. Функция 3. Поэтому, чтобы получить для нее обратную функцию, надо рассмотреть на одном из промежутков монотонности. 4. На отрезке 5. На основании теоремы о существовании и непрерывности обратной функции для функции 6. Значения обратной функции будут лежать на отрезке 7. Обратную функцию обозначают 8. Таким образом, записи 9. Поэтому будут справедливы следующие утверждения:
 является зеркальным отражением графика функции является зеркальным отражением графика функции 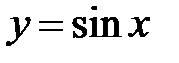 в биссектрисе I и III координатных углов (рис.1). в биссектрисе I и III координатных углов (рис.1).
11. В силу теоремы об обратной функции функция
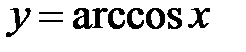 . .
1.Рассмотрим функцию 2. Функция 3. На основании теоремы о существовании и непрерывности обратной функции для функции 4. Значения обратной функции будут лежать на отрезке 5. Обратную функцию обозначают 6.
7. Поэтому будут справедливы следующие утверждения:
 является зеркальным отражением графика функции является зеркальным отражением графика функции  в биссектрисе I и III координатных углов (рис.2). в биссектрисе I и III координатных углов (рис.2).
III. 1. Рассмотрим функцию 2. Функция 3. На основании теоремы о существовании и непрерывности обратной функции для функции 4. Обратную функцию обозначают 5. Таким образом, записи обозначают одно и то же. 6. Поэтому будут справедливы следующие утверждения:
7. График функции  является зеркальным отражением графика функции является зеркальным отражением графика функции  в биссектрисе I и III координатных углов (рис.3). в биссектрисе I и III координатных углов (рис.3).
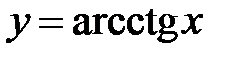 . .
1. Рассмотрим функцию 2. 3. На основании теоремы о существовании и непрерывности обратной функции для функции
 , ,  . .
5. Таким образом, записи 6. Поэтому будут справедливы следующие утверждения:
7. График функции
Модуль Тема №5
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-30; просмотров: 404; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.102.225 (0.037 с.) |
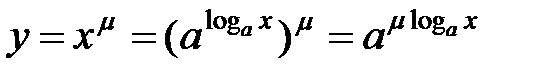 (a > 0)[3].
(a > 0)[3]. . Докажем, что
. Докажем, что

 - любая сходящаяся к нулю справа последовательность значений аргумента
- любая сходящаяся к нулю справа последовательность значений аргумента  . Так как
. Так как  , то из свойств показательной функции вытекает, что
, то из свойств показательной функции вытекает, что  при
при 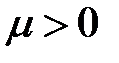 и
и  при
при  . Естественно положить теперь
. Естественно положить теперь  при
при  и считать это выражение неопределенным при
и считать это выражение неопределенным при 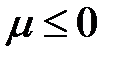 [4].
[4].
 . Для этого достаточно установить, что эта функция непрерывна в каждой точке
. Для этого достаточно установить, что эта функция непрерывна в каждой точке  . Обратимся к формуле
. Обратимся к формуле  . Пусть
. Пусть  – любая сходящаяся слева к
– любая сходящаяся слева к  . Так как логарифмическая функция непрерывна, то последовательность
. Так как логарифмическая функция непрерывна, то последовательность  , где
, где  , сходится к
, сходится к  , причем, все элементы
, причем, все элементы  отличны от
отличны от 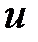 (в самом деле при
(в самом деле при  возрастает и тогда справедливо неравенство, при 0<a<1 логарифмическая функция убывает и тогда
возрастает и тогда справедливо неравенство, при 0<a<1 логарифмическая функция убывает и тогда  ). В силу непрерывности показательной функции последовательность
). В силу непрерывности показательной функции последовательность  сходится к
сходится к  . Иными словами, последовательность
. Иными словами, последовательность 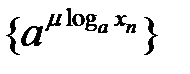 , представляющая собой последовательность
, представляющая собой последовательность  значений степенной функции, соответствующую последовательности
значений степенной функции, соответствующую последовательности  , сходится к
, сходится к  , т. е., к
, т. е., к 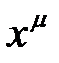 . Непрерывность степенной функции в точке
. Непрерывность степенной функции в точке 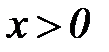 слева доказана. Аналогично доказывается непрерывность этой функции в точке
слева доказана. Аналогично доказывается непрерывность этой функции в точке 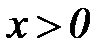 справа. Но непрерывность функции в точке
справа. Но непрерывность функции в точке  , то степенная функция
, то степенная функция 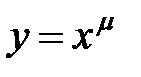 непрерывна также и в точке
непрерывна также и в точке 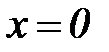 [4].
[4].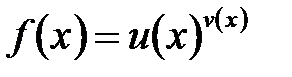 , у которой и основание степени, и показатель являются функциями от
, у которой и основание степени, и показатель являются функциями от 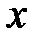 , причем
, причем  при
при  , называется степенно-показательной.
, называется степенно-показательной.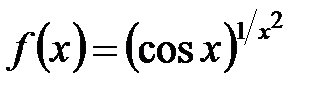 ,
,  .
. , то по определению логарифма можно написать:
, то по определению логарифма можно написать: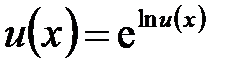 .
. .
.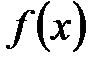 непрерывна во всех точках
непрерывна во всех точках 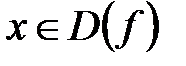 , в которых непрерывны функции
, в которых непрерывны функции  и
и  .
.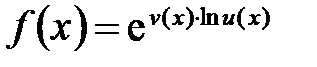 может быть использовано при нахождении пределов.
может быть использовано при нахождении пределов. ,
,  , причем
, причем  , то
, то 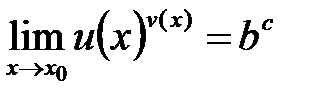 .
. , то
, то
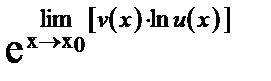
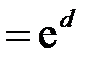 [2].
[2]. ;
; ;
; ;
; ;
; ;
; ;
;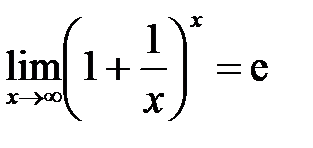 ;
; ;
;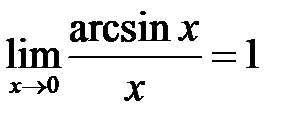 ;
; ;
;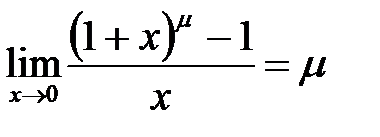 .
. .
.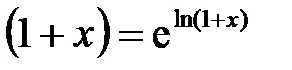 по определению логарифма.
по определению логарифма. :
:  .
. =
= 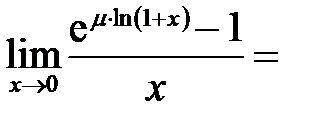
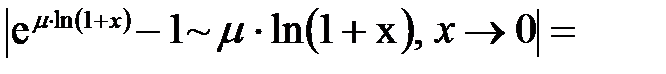

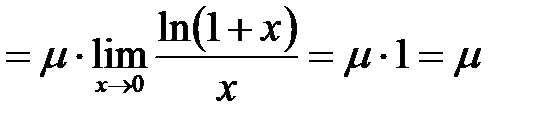 [1].
[1]. .
. .
. не является монотонной на всей числовой прямой.
не является монотонной на всей числовой прямой.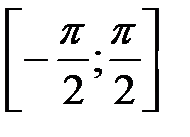 функция
функция  на отрезке
на отрезке 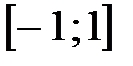 будет существовать обратная функция, в то время как прямая функция будет рассматриваться на отрезке
будет существовать обратная функция, в то время как прямая функция будет рассматриваться на отрезке 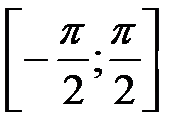 .
. .
. ,
, 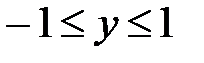 .
.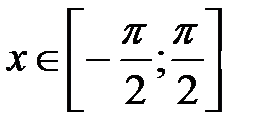 и
и  ,
,  обозначают одно и то же.
обозначают одно и то же. ,
, 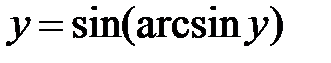 ,
,  .
.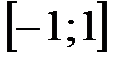 .
. .
. не является монотонной на множестве действительных чисел, но на отрезке
не является монотонной на множестве действительных чисел, но на отрезке 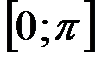 эта функция непрерывна и строго убывает от +1 до -1.
эта функция непрерывна и строго убывает от +1 до -1.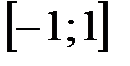 будет существовать обратная функция, в то время как прямая функция будет рассматриваться на отрезке
будет существовать обратная функция, в то время как прямая функция будет рассматриваться на отрезке 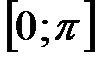 .
. ,
,  Таким образом, записи
Таким образом, записи  и
и  ,
,  обозначают одно и то же.
обозначают одно и то же.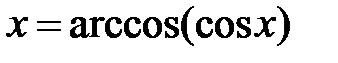 ,
,  ,
,  .
. .
. .
.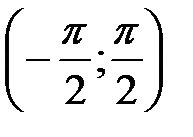 непрерывна и строго возрастает от
непрерывна и строго возрастает от  до
до 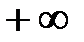 .
. на интервале
на интервале 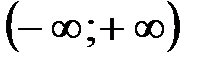 будет существовать обратная функция, в то время как прямая функция будет рассматриваться на интервале
будет существовать обратная функция, в то время как прямая функция будет рассматриваться на интервале  .
. ,
,  и
и 
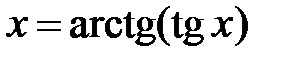 ,
,  ;
; ,
,  .
. .
.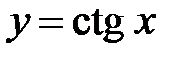 на интервале
на интервале 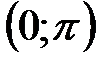 непрерывна и строго убывает на интервале
непрерывна и строго убывает на интервале  .
. на интервале
на интервале 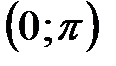 .
. и
и  ,
,  обозначают одно и то же.
обозначают одно и то же.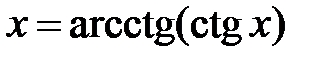 ,
, 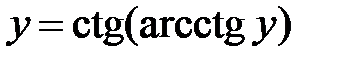 ,
,  является зеркальным отражением графика функции
является зеркальным отражением графика функции 


