
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Функция арифметического корня
Рассмотрим функцию По следствию из второй теоремы Больцано-Коши множество значений функции
Эта функция также непрерывна и строго возрастает на промежутке
Этот график, как и график функции Для любых натуральных значений
В самом деле, в силу свойств степеней с натуральным показателем
При
Чтобы доказать это равенство, достаточно заметить что Если
в такой форме оно верно для любых k, m из множества натуральных чисел. Вместо 1. В соответствии с определением арифметического корня для всех 2. 3. 4. Докажем последнее равенство. Действительно, в соответствии с определением арифметического корня корнем Пусть левая часть доказываемого равенства представляет собой корень Обозначим правую часть этого же равенства за Возведем правую часть равенства, т. е.
На основании первого свойства арифметического корня выражение в прямоугольных скобках есть
Остается доказать, что 5. Действительно, Если
|
|||||
|
Последнее изменение этой страницы: 2016-12-30; просмотров: 422; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.223.106.100 (0.006 с.) |
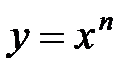 при некотором натуральном n. Она непрерывна и строго возрастает на промежутке
при некотором натуральном n. Она непрерывна и строго возрастает на промежутке  .
. , представляет некоторый промежуток Y. Так как наименьшее значение функции
, представляет некоторый промежуток Y. Так как наименьшее значение функции  при
при  , т. е. справа промежуток Y не ограничен. Следовательно, Y=
, т. е. справа промежуток Y не ограничен. Следовательно, Y=  . Меняя обозначения, можно записать эту функцию и как
. Меняя обозначения, можно записать эту функцию и как . (3)
. (3)
 получается из графика функции
получается из графика функции  , отражением относительно прямой y = x в первом координатном угле (рис.5).
, отражением относительно прямой y = x в первом координатном угле (рис.5). , проходит через начало координат. Кроме того, поскольку
, проходит через начало координат. Кроме того, поскольку 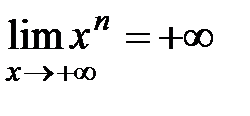 , то и
, то и 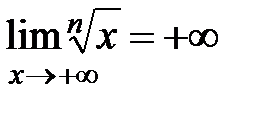 [2].
[2]. и
и  при
при  верно равенство
верно равенство . (4)
. (4) .
. справедливо равенство
справедливо равенство . (5)
. (5) , причем обе части равенства (5) неотрицательны.
, причем обе части равенства (5) неотрицательны. , а
, а  - четное число, обе части равенства (5) определены, но равенство уже может не иметь места. Дело в том, что при нечетном
- четное число, обе части равенства (5) определены, но равенство уже может не иметь места. Дело в том, что при нечетном  в области
в области  имеем
имеем 
 , но
, но  . Поэтому вместо равенства (5) следует писать в этом случае
. Поэтому вместо равенства (5) следует писать в этом случае (6)
(6) пишут также
пишут также 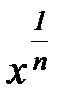 . Отметим некоторые свойства арифметического корня.
. Отметим некоторые свойства арифметического корня. верны равенства
верны равенства  и
и  .
. при
при  .
. при
при  .
. [2]
[2] называется такое число,
называется такое число,  , если
, если  .
.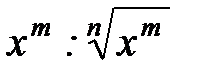 .
. . Если возведем
. Если возведем  , то данное свойство будет доказано.
, то данное свойство будет доказано. .
. , следовательно,
, следовательно,  , значит,
, значит,  есть корень
есть корень 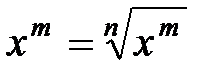 .
. так как по условию арифметического корня
так как по условию арифметического корня 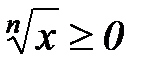 , то
, то  , где
, где  .
. , где
, где  [2].
[2]. уже доказано, докажем
уже доказано, докажем  . Рассмотрим
. Рассмотрим  , тогда
, тогда  .
. , то
, то  можно переписать следующим образом, воспользовавшись правилом возведения в степень при целых показателях, можно записать
можно переписать следующим образом, воспользовавшись правилом возведения в степень при целых показателях, можно записать  , т. е.
, т. е.  является
является 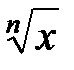 , т.е.
, т.е.  , но
, но  , значит,
, значит,  .
.


