
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
П. 2. Функция корня при n- нечетном
При нечетном n функция и называют корнем n- ой нечетной степени из x. Множество значений этой функции есть также интервал
Отметим также же, что при любом натуральном n и П.3. Степенная функция с положительным рациональным Показателем Определим функцию Любое рациональное положительное число
При таком определении каждому Для степеней с рациональным показателем справедливы все свойства степеней с натуральным показателем: 1. 2. 3. 4. 5. Установим область существования функции (8). При Отметим, что если
Отсюда
В частности, при любом натуральном
При четном Исследуем теперь Если Если и Легко понять теперь, что при
Рассмотрена степенная функция с положительным рациональным показателем
|
|||||
|
Последнее изменение этой страницы: 2016-12-30; просмотров: 399; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.135.246.193 (0.005 с.) |
 , рассмотренная на интервале
, рассмотренная на интервале 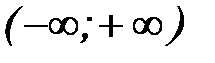 , монотонна уже во всем этом интервале, причем,
, монотонна уже во всем этом интервале, причем, 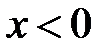 при
при 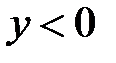 , поэтому теперь она имеет обратную функцию с областью определения
, поэтому теперь она имеет обратную функцию с областью определения 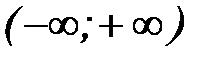 . Эту функцию также обозначают через
. Эту функцию также обозначают через (7)
(7)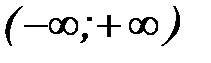 ; она будет, как и функция
; она будет, как и функция  [9].
[9]. График рассматриваемой функции является зеркальным отражением графика функции
График рассматриваемой функции является зеркальным отражением графика функции  в 1-ой и 3-ой координатной плоскости[2].
в 1-ой и 3-ой координатной плоскости[2]. , очевидно
, очевидно  [5].
[5].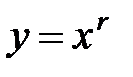 для положительного рационального показателя r.
для положительного рационального показателя r.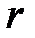 может быть (и притом единственным образом) представлено в виде частного двух взаимно простых натуральных чисел
может быть (и притом единственным образом) представлено в виде частного двух взаимно простых натуральных чисел 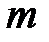 и
и  , т. е.
, т. е.  . Исходя из этого, по определению полагают:
. Исходя из этого, по определению полагают: (8)
(8) , при котором
, при котором  существует, сопоставляется единственное число
существует, сопоставляется единственное число 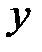 и, следовательно, здесь
и, следовательно, здесь  есть функция от
есть функция от  . Её и называют степенной функцией с положительным рациональным показателем (степенная функция с целым положительным показателем может быть рассмотрена как частный случай (n=1) функции (8), и оговорка, что рациональный показатель r является дробным, излишне) [9].
. Её и называют степенной функцией с положительным рациональным показателем (степенная функция с целым положительным показателем может быть рассмотрена как частный случай (n=1) функции (8), и оговорка, что рациональный показатель r является дробным, излишне) [9].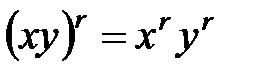 ;
; 
 ;
; ;
; ;
;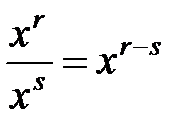 [3].
[3]. - нечетном функция (7) определена на
- нечетном функция (7) определена на 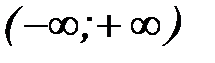 , поэтому при нечетном
, поэтому при нечетном 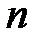 и функция (8) имеет областью существования интервал
и функция (8) имеет областью существования интервал  .Если же
.Если же  - четное число, то прежде всего
- четное число, то прежде всего  - нечетно (иначе дробь
- нечетно (иначе дробь  была бы сократимой). Но функция (7) при четном
была бы сократимой). Но функция (7) при четном 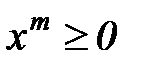 , или, что то же (
, или, что то же ( нечетно)
нечетно)  , т. е. при
, т. е. при  - четном область существования функции (8) есть полусегмент
- четном область существования функции (8) есть полусегмент  .
. , то несущественно, будет ли в определении функции (8)
, то несущественно, будет ли в определении функции (8)  несократимой дробью или нет, ибо тогда при
несократимой дробью или нет, ибо тогда при  (где
(где 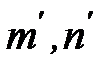 взаимно просты) области существования функций
взаимно просты) области существования функций  и
и  одинаковы и вместе с тем
одинаковы и вместе с тем  и
и  , откуда
, откуда . (9)
. (9)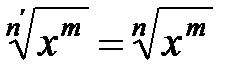 , так как в противном случае в силу монотонности степенной функции было бы
, так как в противном случае в силу монотонности степенной функции было бы  ,что противоречит (9).
,что противоречит (9).
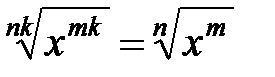 .
. - нечетно) функция (8) является четной:
- нечетно) функция (8) является четной: 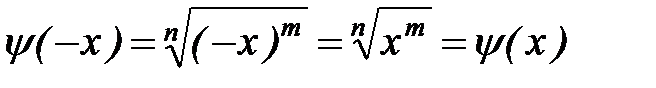 , а при нечетном
, а при нечетном  и нечетном
и нечетном  - нечетной:
- нечетной: 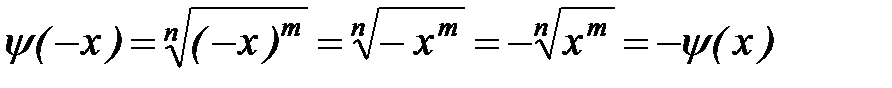 [5].
[5]. на монотонность. Вначале проведём это исследование на
на монотонность. Вначале проведём это исследование на  при натуральном
при натуральном 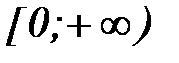 , так, что если
, так, что если 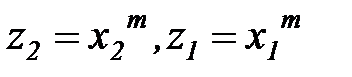 , то при
, то при  и
и  . Но функция
. Но функция  (только обозначением аргумента отличающаяся от функции
(только обозначением аргумента отличающаяся от функции  ) монотонно возрастает на
) монотонно возрастает на  , поэтому при
, поэтому при  и
и  , или
, или  , то есть
, то есть  при
при 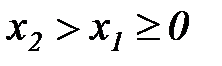 , и, значит,
, и, значит, 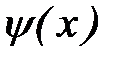 монотонно возрастает на
монотонно возрастает на  . И можно проводить дальнейшее исследование на монотонность.
. И можно проводить дальнейшее исследование на монотонность. , если же
, если же  нечетном и
нечетном и  четном функция (8) не монотонна в
четном функция (8) не монотонна в  , тогда как при
, тогда как при 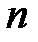 нечетном и
нечетном и  нечетном она монотонно возрастает во всём интервале
нечетном она монотонно возрастает во всём интервале 
 для частного значения
для частного значения  .
. .
.


