Теорема
Пусть функция  определена, строго монотонна и непрерывна на некотором промежутке
определена, строго монотонна и непрерывна на некотором промежутке  , и пусть
, и пусть  - множество её значений. Тогда на множестве
- множество её значений. Тогда на множестве  обратная функция
обратная функция  однозначна, строго монотонна и непрерывна.
однозначна, строго монотонна и непрерывна.
Доказательство
Пусть для определённости функция 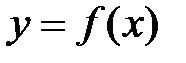 возрастает на
возрастает на  , т.е. для любых
, т.е. для любых  , удовлетворяющих условию
, удовлетворяющих условию  , выполняется неравенство:
, выполняется неравенство:
 (
( ), (
), (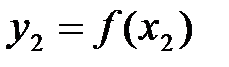 ).
).

1. Докажем однозначность обратной функции.
Однозначность обратной функции  следует из того, что в силу возрастания функции
следует из того, что в силу возрастания функции  на
на  справедливо неравенство:
справедливо неравенство:
 при
при  ,
,
и, значит, каждому  соответствует единственное значение
соответствует единственное значение  .
.
2. Докажем теперь, что обратная функция 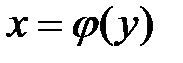 возрастает на
возрастает на  .
.
Действительно, если  , то и
, то и  (
(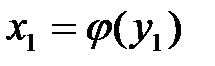 и
и  ), так как если бы было
), так как если бы было  , то из возрастания
, то из возрастания  следовало бы, что
следовало бы, что  , что противоречило бы предположению
, что противоречило бы предположению  . Таким образом, факт строгой монотонности обратной функции
. Таким образом, факт строгой монотонности обратной функции  установлен.
установлен.
3. И, наконец, докажем, что обратная функция  непрерывна на
непрерывна на  .
.
Так как  монотонно возрастает на множестве
монотонно возрастает на множестве  , то она ограничена и принимает наибольшее и наименьшее значения на множестве
, то она ограничена и принимает наибольшее и наименьшее значения на множестве  . Множество
. Множество  является промежутком с концами
является промежутком с концами  и
и  , где
, где  ,
,  .
.
Пусть  ,
,  . Рассмотрим сначала случай, когда
. Рассмотрим сначала случай, когда 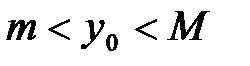 . В этом случае точка
. В этом случае точка  является, очевидно, внутренней точкой промежутка
является, очевидно, внутренней точкой промежутка  .
.
Выберем значение  таким, чтобы
таким, чтобы  и
и  , и положим
, и положим  и
и  . Тогда в силу возрастания
. Тогда в силу возрастания  получим:
получим:
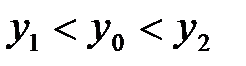 .
.
Возьмём теперь  таким, чтобы выполнялись неравенства:
таким, чтобы выполнялись неравенства:
 и
и  .
.
Тогда, если  удовлетворяет неравенствам
удовлетворяет неравенствам
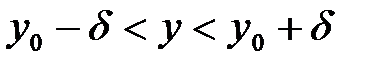 ,
,
то  ,
,
и, следовательно, в силу возрастания  имеем:
имеем:
 .
.
Учитывая, что  и
и  ,
,
получим:  при условии
при условии  .
.
Таким образом, доказано, что для любого достаточно малого  существует
существует  такое, что для всех
такое, что для всех  , удовлетворяющих неравенству
, удовлетворяющих неравенству  , выполняется неравенство
, выполняется неравенство  , т.е. обратная функция
, т.е. обратная функция 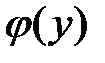 непрерывна в точке
непрерывна в точке  . Но
. Но  - произвольная точка интервала
- произвольная точка интервала  . Значит, обратная функция
. Значит, обратная функция  непрерывна на
непрерывна на 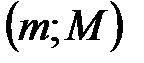 .
.
Если  или
или  , то с помощью аналогичных рассуждений можно доказать непрерывность
, то с помощью аналогичных рассуждений можно доказать непрерывность  справа в точке
справа в точке  и слева в точке
и слева в точке  . Итак, факт непрерывности обратной функции
. Итак, факт непрерывности обратной функции  на
на  доказан.
доказан.
В случае убывания функции  доказательство теоремы проводится аналогично.
доказательство теоремы проводится аналогично.
Модуль
Тема №5
Непрерывность основных
Элементарных функций. Равномерная непрерывность функции на множестве
Лекция №17
1. Непрерывность функций:  ;
;  ;
;  ;
;  ;
;  ;
;  ;
;  ;
; 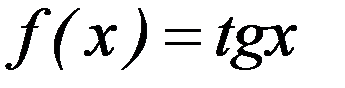 ;
; 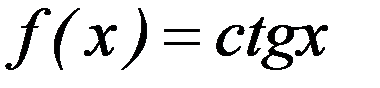 ;
;  .
.
2. Показательная функция во множестве рациональных чисел.
3. Показательная функция во множестве действительных чисел.
ﻫ Непрерывность элементарных функций
1. Доказать, что функция  ,
,  непрерывна в любой точке числовой прямой.
непрерывна в любой точке числовой прямой.
Доказательство
1) Выберем произвольную точку 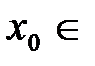 R, так как
R, так как  определена на R.
определена на R.
2) Для этой точки  R определим предел и значение функции в точке
R определим предел и значение функции в точке  :
:
а)  ,
,
б) 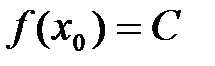 .
.
3) Следовательно,  , т.е. функция
, т.е. функция  непрерывна в произвольной точке
непрерывна в произвольной точке  .
.
4) Так как точка  выбиралась произвольно, то функция
выбиралась произвольно, то функция  ,
,
 непрерывна в каждой точке числовой прямой.
непрерывна в каждой точке числовой прямой.
5) Доказательство проведено на основании определения №1 непрерывности функции в точке. Ч.т.д.
2. Доказать, что функция  непрерывна в любой точке числовой прямой, кроме нуля, т.е.
непрерывна в любой точке числовой прямой, кроме нуля, т.е.  R \0.
R \0.
Доказательство
1) Доказательство проведем на основании определения №5 непрерывности функции в точке на языке приращений.
2) Выберем произвольную точку  R \0, так как функция определена на R \0, и определим в ней приращение функции:
R \0, так как функция определена на R \0, и определим в ней приращение функции:

 .
.
3) Вычислим предел
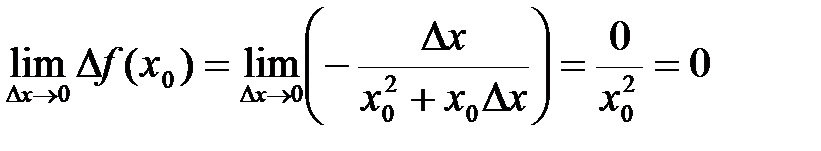 ,
,
так как  . Значит, функция
. Значит, функция  непрерывна в произвольной точке
непрерывна в произвольной точке  .
.
4) Так как точка  выбиралась произвольно, то функция
выбиралась произвольно, то функция  непрерывна в любой точке
непрерывна в любой точке  R \0. Ч.т.д.
R \0. Ч.т.д.
3. Доказать, что функция  непрерывна в любой точке множества действительных чисел.
непрерывна в любой точке множества действительных чисел.
Доказательство
1) Область определения функции – множество действительных чисел.
2) Выберем произвольную точку  R и определим в ней приращение функции:
R и определим в ней приращение функции:
 .
.
3) Вычислим предел  . Значит, функция
. Значит, функция  непрерывна в произвольной точке
непрерывна в произвольной точке  .
.
4) Так как точка  выбиралась произвольно, то функция
выбиралась произвольно, то функция  непрерывна в любой точке множества действительных чисел.
непрерывна в любой точке множества действительных чисел.
5) Доказательство проведено на основании определения №5 непрерывности функции в точке на языке приращений. Ч.т.д.
4. Доказать, что функция  непрерывна в любой точке множества R.
непрерывна в любой точке множества R.
Доказательство
Доказательство следует из теоремы о непрерывности алгебраической суммы, произведения и частного непрерывных функций и непрерывности функции  в любой точке числовой оси. Ч.т.д.
в любой точке числовой оси. Ч.т.д.
5. Доказать, что функция  непрерывна в любой точке множества действительных чисел, за исключением тех точек, где знаменатель дроби обращается в нуль.
непрерывна в любой точке множества действительных чисел, за исключением тех точек, где знаменатель дроби обращается в нуль.
Доказательство
Доказательство следует из теоремы о непрерывности алгебраической суммы, произведения и частного непрерывных функций и непрерывности функций
 и
и  .
.
Значит, заданная функция непрерывна в любой точке множества R, исключая те точки, в которых знаменатель равен нулю. Ч.т.д.
6. Доказать, что функция  непрерывна в любой точке числовой прямой.
непрерывна в любой точке числовой прямой.
Доказательство
1) Доказательство проведем на основании определения №5 непрерывности функции в точке на языке приращений.
2) Функция  определена в любой точке числовой прямой.
определена в любой точке числовой прямой.
3) Выберем произвольную точку  R и определим приращение функции в этой точке:
R и определим приращение функции в этой точке:
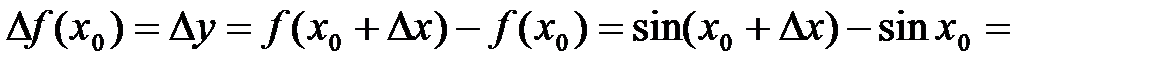
 .
.
4) Вычислим предел от приращения функции:
 .
.
Значит, функция  непрерывна в произвольной точке
непрерывна в произвольной точке  .
.
5) Так как точка  выбиралась произвольно, то функция
выбиралась произвольно, то функция  непрерывна в любой точке числовой прямой. Ч.т.д.
непрерывна в любой точке числовой прямой. Ч.т.д.
7. Аналогично доказывается непрерывность функции  в любой точке числовой оси. Провести доказательство самостоятельно.
в любой точке числовой оси. Провести доказательство самостоятельно.
8. Из непрерывности функций  и
и  в любой точке числовой прямой по теореме о непрерывности частного непрерывных функций в точке следует непрерывность функции
в любой точке числовой прямой по теореме о непрерывности частного непрерывных функций в точке следует непрерывность функции
а)  ;
;  во всех точках числовой прямой, кроме точек
во всех точках числовой прямой, кроме точек
 ,
,  - любое целое число;
- любое целое число;
б) а также непрерывность функции  и
и  во всех точках, кроме точек
во всех точках, кроме точек  , где
, где  - любое целое число.
- любое целое число.
9. Доказать, что функция 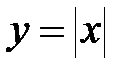 непрерывна на всей числовой прямой.
непрерывна на всей числовой прямой.
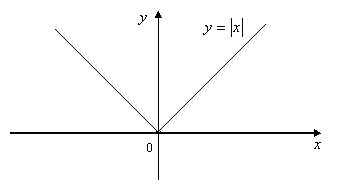
Доказательство
1) На интервале  функция
функция  имеет вид
имеет вид  , так как
, так как  . А эта функция непрерывна в каждой точке числовой прямой.
. А эта функция непрерывна в каждой точке числовой прямой.
2) На интервале  функция
функция  имеет вид
имеет вид  , так как
, так как  . А эта функция непрерывна как произведение двух непрерывных функций
. А эта функция непрерывна как произведение двух непрерывных функций  и
и  .
.
3) Остаётся установить непрерывность функции  в точке
в точке  .
.
4) Для этого вычислим односторонние пределы в точке  :
:
а)  ; б)
; б)  .
.
5) Так как  и
и  , то функция
, то функция  непрерывна в точке
непрерывна в точке  . А, следовательно, она непрерывна на всей числовой прямой.
. А, следовательно, она непрерывна на всей числовой прямой.
Ч.т.д.
Вывод:
1.Все рассмотренные функции непрерывны в областях их существования.
2.На основании теорем непрерывности суммы, разности, произведения и частного непрерывных функций можно утверждать, что функции, получаемые при помощи конечного числа арифметических действий над непрерывными функциями, также являются непрерывными функциями в области их существования.
Показательная функция во множестверациональных чисел
Определение 1.Пусть  , тогда для любого рационального числа
, тогда для любого рационального числа  будет определено значение
будет определено значение  . Тем самым определена функция
. Тем самым определена функция  . Эту функцию называют показательной на множестве рациональных чисел.
. Эту функцию называют показательной на множестве рациональных чисел.
Свойства показательной функции
I.  ,
,  ,
,  , т.е.
, т.е.  , где
, где  ,
,  .1.Пусть
.1.Пусть  . Тогда:a) если
. Тогда:a) если  , то
, то  ;б) если
;б) если  , то
, то  .2.а)
.2.а)  ;б)
;б)  ;в)
;в)  .3.
.3.  .4.
.4.  .5.
.5.  , для любого рационального числа
, для любого рационального числа  :
:  .
.
Док-во: 5-ого свойства1. Если  и
и  , то в силу первого свойства:
, то в силу первого свойства:  .
.
2. Так как  , а
, а  , то
, то  .3. На основании второго свойства:
.3. На основании второго свойства:  ,
,  и
и  , следовательно,
, следовательно,  .4. Аналогично доказывается неравенство
.4. Аналогично доказывается неравенство  при
при  .
.
II.Лемма 1.Пусть  . Тогда
. Тогда  существует
существует  , что для всех рациональных чисел
, что для всех рациональных чисел  , удовлетворяющих неравенству
, удовлетворяющих неравенству  выполняется неравенство:
выполняется неравенство:  . Справка:
. Справка:  при
при  .
.
Док-во: I.1. Пусть  .
.
2. Так как  , то
, то  :
: 

 и
и  .3. Так как
.3. Так как  , то на основании первого свойства
, то на основании первого свойства  , следовательно, два двойных неравенства можно переписать так:
, следовательно, два двойных неравенства можно переписать так:

4. Пусть  -- рациональное число такое, что
-- рациональное число такое, что  , то есть
, то есть  .5.Тогда на основании первого свойства показательной функции можно написать:
.5.Тогда на основании первого свойства показательной функции можно написать:  или
или  или
или  .II. При
.II. При  лемма очевидна.III. При
лемма очевидна.III. При  лемма доказывается аналогично, только в соответствии с неравенством первого свойства знак надо заменить на обратный (случай 1б).
лемма доказывается аналогично, только в соответствии с неравенством первого свойства знак надо заменить на обратный (случай 1б).
2 Показательная функция во множестве действительных чисел
Определение2.Пусть  , а
, а  -- произвольное действительное число, то есть
-- произвольное действительное число, то есть  . Пусть
. Пусть  -- последовательность рациональных чисел, сходящаяся к
-- последовательность рациональных чисел, сходящаяся к  . Очевидно, что для
. Очевидно, что для  такая последовательность всегда существует. Тогда всегда существует и не зависит от выбора последовательности
такая последовательность всегда существует. Тогда всегда существует и не зависит от выбора последовательности  ,
,  ,
,  .
.
Случай  не представляет интереса для изучения, так как
не представляет интереса для изучения, так как  .
.
Теорема1.Показательная функция во множестве действительных чисел  ,
,  ,
,  обладает следующими свойствами:1) непрерывна в каждой точке числовой прямой;2) при
обладает следующими свойствами:1) непрерывна в каждой точке числовой прямой;2) при  строго возрастает, а при
строго возрастает, а при  строго убывает на всей числовой прямой;3)
строго убывает на всей числовой прямой;3)  ,
,  ;4)
;4)  ,
,  ;5)а) при
;5)а) при 
 ;б) при
;б) при 
 ;6)а) при
;6)а) при 
 ;б) при
;б) при 
 .
.
Док-во: 1-ого свойства1. Известно, что  :
:  .2. Это утверждение справедливо и для действительных чисел.3. Пусть
.2. Это утверждение справедливо и для действительных чисел.3. Пусть  -- произвольное действительное число,
-- произвольное действительное число,  , и
, и  ,
,  , -- показательная функция во множестве действительных чисел.4. Найдем приращение функции
, -- показательная функция во множестве действительных чисел.4. Найдем приращение функции  в точке
в точке  при изменении аргумента на
при изменении аргумента на  :
:  .
.
5. Согласно лемме для показательной функции во множестве рациональных чисел:  , удовлетворяющих неравенству
, удовлетворяющих неравенству  ), выпоняется неравенство:
), выпоняется неравенство:  , причем при
, причем при  ,
, 
 .6. Умножим обе части неравенства пункта 5 на положительное число
.6. Умножим обе части неравенства пункта 5 на положительное число  :
:  .7. Сравним приращение функции и последнее неравенство, очевидно, что
.7. Сравним приращение функции и последнее неравенство, очевидно, что  при
при  , т.е.
, т.е.  , то есть на основании определения №5 непрерывности функции в точке, функция
, то есть на основании определения №5 непрерывности функции в точке, функция  непрерывна в точке
непрерывна в точке  .8. Так как точка
.8. Так как точка  выбиралась произвольно, то функция
выбиралась произвольно, то функция  непрерывна в любой точке числовой прямой.
непрерывна в любой точке числовой прямой.
Док-во: 2-ого свойства1. Пусть для определенности  и
и  .2. В силу плотности рациональных чисел во множестве действительных чисел существуют такие рациональные числа
.2. В силу плотности рациональных чисел во множестве действительных чисел существуют такие рациональные числа  и
и  , что
, что

3. Выберем некоторые две последовательности рациональных чисел  и
и  так, чтобы
так, чтобы  и
и  , и чтобы
, и чтобы  для
для  .4. При
.4. При  на основании первого свойства показательной функции во множестве рациональных чисел можно записать:
на основании первого свойства показательной функции во множестве рациональных чисел можно записать:

5. Перейдем к пределу при  (в показателях степеней) в последнем неравенстве:
(в показателях степеней) в последнем неравенстве:  ;
;  ;
;  ;
;  , следовательно, на основании определения показательной функции во множестве действительных чисел:
, следовательно, на основании определения показательной функции во множестве действительных чисел:  ;
;  ;
;  .6. Неравенство пункта 4 примет вид:
.6. Неравенство пункта 4 примет вид:  или
или  при
при  .7. А на основании определения возрастающей функции при
.7. А на основании определения возрастающей функции при 
 , следовательно,
, следовательно,  строго возрастает при
строго возрастает при  .
.
Замечание1.Случай  рассматривается аналогично.
рассматривается аналогично.
Замечание2.Графики функции имеют вид: 
Док-во: 3-его свойства1. Пусть  и
и  такие последовательности рациональных чисел, что
такие последовательности рациональных чисел, что  ,
,  и, следовательно,
и, следовательно,  на основании теоремы о пределе суммы двух сходящихся последовательностей.2. Тогда в силу определения показательной функции во множестве действительных чисел
на основании теоремы о пределе суммы двух сходящихся последовательностей.2. Тогда в силу определения показательной функции во множестве действительных чисел  .3. По свойству №2 показательной функции во множестве рациональных чисел
.3. По свойству №2 показательной функции во множестве рациональных чисел  , следовательно,
, следовательно, 
 , a>0.
, a>0.
Следствие 1. Для любых действительных чисел  справедливо равенство:
справедливо равенство:  , следовательно,
, следовательно,  . 2. Поэтому
. 2. Поэтому  .
.
Док-во: 4-ого свойства
I.1. Пусть  -- целое положительное число,
-- целое положительное число,  , т.е.
, т.е.  .2. Применим
.2. Применим  раз свойство №2 показательной функции во множестве рациональных чисел:
раз свойство №2 показательной функции во множестве рациональных чисел:  Следовательно,
Следовательно,  .
.
II.1. Пусть  ,
,  , где
, где  -- целое положительное число,
-- целое положительное число,  .2. Докажем, что:
.2. Докажем, что:  , т.е. что
, т.е. что  -- есть корень степени
-- есть корень степени  из числа
из числа  :
:  .3. На основании равенства
.3. На основании равенства  и по определению корня: если
и по определению корня: если  , то
, то  . Или
. Или  . Следовательно,
. Следовательно,  .
.
III.1. Пусть  ,
,  , где
, где  .2. По раннее доказанному можно написать:
.2. По раннее доказанному можно написать:  . Следовательно,
. Следовательно,  .
.
IV. Пусть теперь  ,
,  , то
, то  . Следовательно,
. Следовательно,  .
.
V. Очевидно, что  .Вывод: таким образом, доказано, что
.Вывод: таким образом, доказано, что  ,
,  :
:  .
.
VI.1. Пусть  .2. Рассмотрим произвольную последовательность рациональных чисел
.2. Рассмотрим произвольную последовательность рациональных чисел  , сходящуюся к
, сходящуюся к  :
:  .3. Тогда в силу равенства
.3. Тогда в силу равенства  будет иметь место:
будет иметь место:

4. Поскольку  , то в соответствии с определением показательной функции во множестве действительных чисел можно записать:а)
, то в соответствии с определением показательной функции во множестве действительных чисел можно записать:а)  ;б)
;б)  , так как
, так как  .5. Перейдем к пределу в равенстве пункта 3 при
.5. Перейдем к пределу в равенстве пункта 3 при  :
:

6. В соответствии с пунктом 4 перепишем записанное равенство:  ,
,  .
.
Док-во: 5-ого свойстваI.1. Докажем, что при 
 .2. Пусть
.2. Пусть  .3. Тогда
.3. Тогда  ,
,  .4.Так как
.4.Так как  , то
, то  (в соответствии с неравенством Бернулли).5. Для
(в соответствии с неравенством Бернулли).5. Для  ,
,  , что
, что  .6. Если
.6. Если  , а
, а  , то при
, то при 
 , следовательно,
, следовательно,  -- определение бесконечно большой функции при
-- определение бесконечно большой функции при  (бесконечный предел функции на бесконечности) равносильно
(бесконечный предел функции на бесконечности) равносильно  .
.
II.1. Если  , то
, то  выполняется
выполняется  .2. Так как
.2. Так как  , то
, то  , т.е.
, т.е.  .3. Поэтому
.3. Поэтому  .4. Если
.4. Если  и
и  , то
, то  , следовательно, подавно
, следовательно, подавно  на основании теоремы о сжатой переменной.
на основании теоремы о сжатой переменной.
Док-во: 6-ого свойства1. При 
 .2. При
.2. При 
 .Доказательство проводится аналогично доказательству свойства №5.
.Доказательство проводится аналогично доказательству свойства №5.
Модуль
Тема №5


 определена, строго монотонна и непрерывна на некотором промежутке
определена, строго монотонна и непрерывна на некотором промежутке  , и пусть
, и пусть  - множество её значений. Тогда на множестве
- множество её значений. Тогда на множестве  однозначна, строго монотонна и непрерывна.
однозначна, строго монотонна и непрерывна.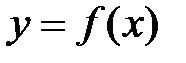 возрастает на
возрастает на  , т.е. для любых
, т.е. для любых  , удовлетворяющих условию
, удовлетворяющих условию  , выполняется неравенство:
, выполняется неравенство: (
( ), (
), (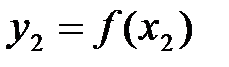 ).
).
 следует из того, что в силу возрастания функции
следует из того, что в силу возрастания функции  на
на  при
при  ,
, соответствует единственное значение
соответствует единственное значение  .
.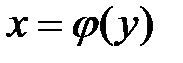 возрастает на
возрастает на  .
. , то и
, то и  (
(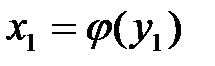 и
и  ), так как если бы было
), так как если бы было  , то из возрастания
, то из возрастания  следовало бы, что
следовало бы, что  , что противоречило бы предположению
, что противоречило бы предположению  . Таким образом, факт строгой монотонности обратной функции
. Таким образом, факт строгой монотонности обратной функции  установлен.
установлен. непрерывна на
непрерывна на  монотонно возрастает на множестве
монотонно возрастает на множестве  и
и  , где
, где  ,
,  .
. ,
,  . Рассмотрим сначала случай, когда
. Рассмотрим сначала случай, когда 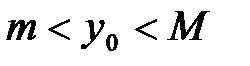 . В этом случае точка
. В этом случае точка  является, очевидно, внутренней точкой промежутка
является, очевидно, внутренней точкой промежутка  .
. таким, чтобы
таким, чтобы  и
и  , и положим
, и положим  и
и  . Тогда в силу возрастания
. Тогда в силу возрастания  получим:
получим: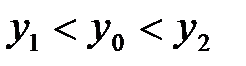 .
. таким, чтобы выполнялись неравенства:
таким, чтобы выполнялись неравенства: и
и  .
. удовлетворяет неравенствам
удовлетворяет неравенствам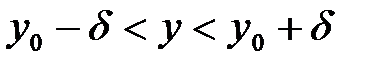 ,
, ,
, имеем:
имеем: .
. и
и  ,
, при условии
при условии  .
. существует
существует  такое, что для всех
такое, что для всех  , удовлетворяющих неравенству
, удовлетворяющих неравенству  , выполняется неравенство
, выполняется неравенство  , т.е. обратная функция
, т.е. обратная функция 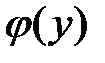 непрерывна в точке
непрерывна в точке  . Но
. Но  - произвольная точка интервала
- произвольная точка интервала  . Значит, обратная функция
. Значит, обратная функция  непрерывна на
непрерывна на 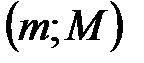 .
. или
или  , то с помощью аналогичных рассуждений можно доказать непрерывность
, то с помощью аналогичных рассуждений можно доказать непрерывность  справа в точке
справа в точке  и слева в точке
и слева в точке  . Итак, факт непрерывности обратной функции
. Итак, факт непрерывности обратной функции  на
на  доказан.
доказан. доказательство теоремы проводится аналогично.
доказательство теоремы проводится аналогично. ;
;  ;
;  ;
;  ;
;  ;
;  ;
;  ;
; 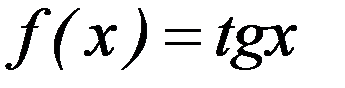 ;
; 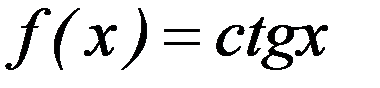 ;
;  .
. ,
,  непрерывна в любой точке числовой прямой.
непрерывна в любой точке числовой прямой.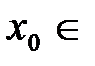 R, так как
R, так как  R определим предел и значение функции в точке
R определим предел и значение функции в точке  :
: ,
,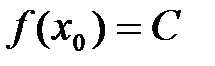 .
. , т.е. функция
, т.е. функция  непрерывна в произвольной точке
непрерывна в произвольной точке  .
. непрерывна в любой точке числовой прямой, кроме нуля, т.е.
непрерывна в любой точке числовой прямой, кроме нуля, т.е.  R \0.
R \0. R \0, так как функция определена на R \0, и определим в ней приращение функции:
R \0, так как функция определена на R \0, и определим в ней приращение функции:
 .
.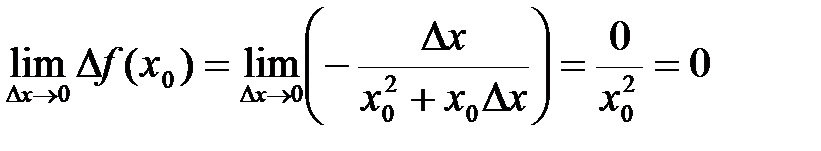 ,
, . Значит, функция
. Значит, функция  выбиралась произвольно, то функция
выбиралась произвольно, то функция  непрерывна в любой точке
непрерывна в любой точке  непрерывна в любой точке множества действительных чисел.
непрерывна в любой точке множества действительных чисел. .
. . Значит, функция
. Значит, функция  непрерывна в любой точке множества действительных чисел.
непрерывна в любой точке множества действительных чисел. непрерывна в любой точке множества R.
непрерывна в любой точке множества R. непрерывна в любой точке множества действительных чисел, за исключением тех точек, где знаменатель дроби обращается в нуль.
непрерывна в любой точке множества действительных чисел, за исключением тех точек, где знаменатель дроби обращается в нуль. непрерывна в любой точке числовой прямой.
непрерывна в любой точке числовой прямой. R и определим приращение функции в этой точке:
R и определим приращение функции в этой точке: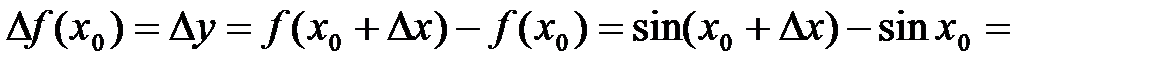
 .
. .
. в любой точке числовой оси. Провести доказательство самостоятельно.
в любой точке числовой оси. Провести доказательство самостоятельно. и
и  в любой точке числовой прямой по теореме о непрерывности частного непрерывных функций в точке следует непрерывность функции
в любой точке числовой прямой по теореме о непрерывности частного непрерывных функций в точке следует непрерывность функции ;
;  во всех точках числовой прямой, кроме точек
во всех точках числовой прямой, кроме точек ,
,  - любое целое число;
- любое целое число; и
и  во всех точках, кроме точек
во всех точках, кроме точек  , где
, где 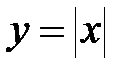 непрерывна на всей числовой прямой.
непрерывна на всей числовой прямой.
 функция
функция  имеет вид
имеет вид  , так как
, так как  . А эта функция непрерывна в каждой точке числовой прямой.
. А эта функция непрерывна в каждой точке числовой прямой. функция
функция  имеет вид
имеет вид  , так как
, так как  . А эта функция непрерывна как произведение двух непрерывных функций
. А эта функция непрерывна как произведение двух непрерывных функций  и
и  .
. в точке
в точке  .
. :
: ; б)
; б)  .
. и
и  , то функция
, то функция  непрерывна в точке
непрерывна в точке  . А, следовательно, она непрерывна на всей числовой прямой.
. А, следовательно, она непрерывна на всей числовой прямой.


