
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Кинематический анализ механизмов
При кинематическом анализе механизма движение входных звеньев задано и определяются положения, траектории, скорости и ускорения выходных и промежуточных звеньев. Полученные кинематические характеристики механизма используются при динамическом анализе, когда определяются силы, действующие на звенья. Определение положения звеньев и построение траекторий отдельных точек звеньев получают последовательным построением различных положений элементов механизма. Например, циклическое движение входного звена кривошипа разбивают на равные промежутки – на 6 или 12 частей. Затем достраивают к положениям кривошипа положения других звеньев механизма. Построения выполняют в масштабе: Полученный чертеж положений звеньев механизма, соответствующих полному циклу его движения, называют планом положений механизма. Непрерывные линии, соединяющие последовательные положения одноименных точек дают различные траектории движения этих точек. План положений механизма и траектории движений точек определяют размеры и занимаемую площадь механизмов и являются основой для последующего анализа скоростей и ускорений звеньев (кинематический анализ). Определение основных кинематических характеристик механизма - линейных и угловых скоростей и ускорений звеньев выполняют аналитическим, графическим и графоаналитическим методами. Аналитический метод имеет высокую точность решения, но очень трудоемок. Поэтому для его реализации широко применяется вычислительная техника, например, для механизмов роботов и манипуляторов. Два других метода – графический и графоаналитический - просты и наглядны. Графический метод определения скоростей и ускорений осуществляется с помощью графического дифференцирования диаграммы перемещений, получаемой из плана положений механизма. Графический метод Общие положения Построение планов положений механизма начинается с построения нулевого положения и крайнего левого положения ползуна (рисунок 1.17). Затем траекторию кривошипа (траектория точки А) разбивают на несколько равных частей, соответствующих равным интервалам времени (6, 12 или 24) (рисунок 1.18). Соединяя точку О1 с различными положениями, получаем соответствующие положения кривошипа Ао, А1, А2,…А6. Методом засечек осуществляем разметку следующих звеньев – 3, 4 и 5 и строим их положения Во, В1, В2,…; Со, С1, С2,… Диаграмма перемещения точки С является графическим изображением закона ее движения. Построив 6 планов положения механизма, получим 6 положений точки С выходного звена. Проводим оси координат (рисунок 1.19, а).
По оси абсцисс откладываем отрезок
где n1 – частота вращения выходного звена, мин-1; ω1 – угловая скорость входного звена, с-1. Масштабный коэффициент времени:
где Отрезок
Рисунок 1.17
Рисунок 1.18 Если перемещения Диаграммы скорости Построение диаграммы скорости точки С осуществляется методом графического дифференцирования диаграммы перемещения (метод хорд). Проводим новую систему координат (рисунок 1.19, б). Ось абсцисс проложим влево относительно начала координат и отложим на ней отрезок произвольной длины Н1 (мм) до точки Р1. Точка Р1 называется полюсом графического дифференцирования (Н1 = 20 мм). На диаграмме перемещения, на первом участке, соединяем точки 0 и 1 хордой (рисунок 1.19, а). Из полюса Р1 проводим линию
где Истинные приращения функции и аргумента
Подставим эти значения в равенство (1.7)
то есть, Vср – средняя скорость на первом участке:
Поскольку величина
Масштабный коэффициент скорости
Рисунок 1.19
Соединяем точки 1 и 2 хордой на втором участке диаграммы перемещения. Из полюса Р1 проводим линию Р12′ параллельно хорде 1 2. Отрезок Диаграммы ускорения Построение диаграммы ускорения точки С осуществляется методом графического дифференцирования диаграммы скорости. Для этого проводится новая система координат (рисунок 1.19, в). Выбирается полюс графического дифференцирования Р2 на расстоянии Н2 от начала координат (Н2 = 15 мм). На диаграмме скорости (рисунок 1.19, б) соединяются хордами точки пересечения диаграммы скорости с отметками времени на каждом участке. Из точки Р2 проводятся линии параллельные хордам. По аналогии отрезок
Масштабный коэффициент диаграммы ускорения:
Истинные значения перемещения, скорости и ускорения пятого звена, например, для III положения механизма
1.2.2Графоаналитический метод Общие положения Для плоских механизмов, в частности рычажных, кинематический анализ удобно выполнять методом планов скоростей и ускорений. План скоростей (или ускорений) - это векторная картина скоростей (ускорений) характерных точек механизма для данного его положения. Метод планов имеет два существенных преимущества: во-первых, не нужно выполнять операции дифференцирования, уравнения для искомых величин получают непосредственно на основе теорем механики; во-вторых, можно очень наглядно интегрировать решение в графическом виде. Метод планов основан на следующих теоремах теоретической механики. Теорема 1. При плоском движении твердого тела его мгновенное абсолютное перемещение можно представить (рисунок 1.20) как сумму переносного поступательного перемещения вместе с любой точкой А этого тела и относительного вращения вокруг оси, проходящей через ту же точку А. (Именно так можно рассматривать перемещение тела на плоскости из положения АоВо через промежуточное положение АВ’ в положение АВ). Теорема 2. Абсолютная скорость, υа движущейся точки в каждый момент времени равна векторной сумме переносной υе и относительной υr скоростей:
Теорема 3 (Кориолиса). Абсолютное ускорение аа в сложном движении равно геометрической сумме переносного ае, относительного аr и кориолисова аk ускорений:
Направление Кориолисова ускорения – вектор направления скорости
где ωе – угловая скорость переносного движения; υr – относительная линейная скорость; произведение ωе и υr - векторное. Объединяя утверждения теорем 1 и 2, для абсолютной скорости любой точки В можно записать следующее векторное равенство:
где υА – скорость любой точки А рассматриваемого твердого тела; υВА - относительная скорость точки В в ее мгновенном вращении вокруг точки А; линия действия этой скорости перпендикулярна радиусу ВА. Графическое изображение скоростей в масштабе называют планом скоростей. Точка Рv является началом отсчета, и ее часто называют полюсом плана скоростей. Если переносное движение – поступательное (ωе = 0), то ускорение Кориолиса аk = 0. Относительное движение по теореме 1 - вращательное движение точки В вокруг точки А. Поэтому относительное ускорение аr, в свою очередь состоит из двух ускорений: нормального аn = ω2r, направленного вдоль линии ВА к центру вращения, и касательного аt, направленного перпендикулярно ВА (рисунок 1.20, аr = aВА). Таким образом, выражение (1.12) получит вид:
Рассмотрим векторный метод планов скоростей и ускорений на примере четырехшарнирного механизма (рисунок 1.21, а). План скоростей Абсолютная скорость точки А
Рисунок 1.21
Векторное уравнение (1.14) определяет абсолютную скорость точки В; здесь линия действия вектора который показывает, что каждый миллиметр чертежа изображает μυ единиц скорости; единица масштабного коэффициента – (м/с)/мм.
Продолжая графическое решение уравнения (1.14), из точки а плана (рисунок 1.21, б), которая изображает конец вектора
Угловые скорости звеньев 2 и 3 в их движении относительно точек А и О1, 1/с:
где l 2 = АВ, l 3 = ВО1 – длины соответствующих звеньев. Для определения направления угловых скоростей ω2 и ω3 векторы Определив скорость точки В, скорости точек С и М (или любых других в данном положении механизма) находят без составления уравнений и их решения; для этого используются следующие свойства планов скоростей и ускорений: 1. Векторы, идущие из точки р υ плана скоростей (ускорений), представляют собой в масштабе μυ абсолютные скорости (ускорения) соответствующих точек механизма; векторы, не проходящие через полюс, есть относительные скорости (ускорения) точек звеньев. Концы векторов абсолютных скоростей (ускорений) точек А, В, … принято обозначать соответствующими малыми буквами а, b, …. 2. Отображения точек закрепленных шарниров О, О1 всегда совпадают с начальной точкой р υ. 3. Отрезки оа, ab, o1b на плане отображают звенья АО, АВ и О1В механизма. Это означает, что если, например, на звене АВ (рисунок 1.21, а) имеется точка С, лежащая на прямой АВ, то соответствующая отображающая точка с на плане (рисунок 1.21, б) находится на прямой ab и при этом верно соотношение ab/ac=l2/АС, что вытекает из уравнений
4. Любые три точки А, В, М звена, составляющие треугольник, отображаются на плане в треугольник Δabm подобный ΔАВМ; на отрезке ab можно построить два треугольника, подобных данному; из них искомое решение дает тот, у которого порядок обхода вершин из точки а такой же, как в ΔАМВ (направление обхода вершин на звене и на плане должно быть одинаковым). Таким образом, на рисунке 1.21, б получено отображение на плане точки М – точки m:
При тщательном выполнении построений, средняя ошибка определения скоростей составляет 5…7%, ускорений – до 10%. План ускорений Исходными данными для построения плана ускорений механизма (рисунок 1.21, в) являются известные абсолютные ускорения точки А звена 1 и найденные скорости. Ускорение точки А при
Выбрав начало отсчета ра плана ускорений (рисунок 1.21, в), показывают на чертеже отображения ускорений
Для определения ускорения точки В рассмотрим абсолютное движение звена АВ как сумму переносного и относительного движений. С учетом выражения (1.15) векторной уравнение абсолютного ускорения точки В получит вид:
Вектор нормального ускорения Точка В принадлежит одновременно звеньям АВ и ВО1 (рисунок 1.21, а). Рассматривая движение звена ВО1 и принимая за полюс неподвижную точку О1, запишем следующее уравнение для абсолютного ускорения точки В:
где нормальное ускорение Совместное решение векторных уравнений (1.18) и (1.19) дает возможность определить искомый вектор абсолютного ускорения точки В. Отрезок Аналогично, графически реализуется уравнение (1.19). На пересечении линий действия векторов Если на звене имеется дополнительная точка, например, на звене 2 точка С, то ее отображение с на плане ускорений (рисунок 1.21, в) находится на отрезке ab с учетом соблюдения условия Отображение m точки М строится на основании четвертого свойства планов: Угловые ускорения звеньев в их относительном вращательном движении можно найти, используя соответствующие касательные ускорения, 1/с2: Для определения направления углового ускорения ε2 звена АВ переносим вектор
|
|||||||||
|
Последнее изменение этой страницы: 2017-01-19; просмотров: 136; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.119.105.239 (0.045 с.) |
 м/мм или
м/мм или  м/мм.
м/мм. произвольной длины, представляющий собой в масштабе μt время t(с) одного периода (время одного полного оборота выходного звена)
произвольной длины, представляющий собой в масштабе μt время t(с) одного периода (время одного полного оборота выходного звена)

 = 120 мм – отрезок на чертеже (рисунок 1.19, а).
= 120 мм – отрезок на чертеже (рисунок 1.19, а).

 ,
,  и так далее на графике перемещения (рисунок 1.19, а) откладывать прямо с плана положений механизма (рисунок 1.18), то масштабный коэффициент диаграмм перемещения будет равен масштабному коэффициенту плана положений
и так далее на графике перемещения (рисунок 1.19, а) откладывать прямо с плана положений механизма (рисунок 1.18), то масштабный коэффициент диаграмм перемещения будет равен масштабному коэффициенту плана положений  .
. параллельно хорде 01. Из подобия треугольников 0I1 (рисунок 1.19, а) и Р101' (рисунок 1.19, б) следует
параллельно хорде 01. Из подобия треугольников 0I1 (рисунок 1.19, а) и Р101' (рисунок 1.19, б) следует , (1.7)
, (1.7) Δ
Δ  и Δ
и Δ  - приращение функции и аргумента, построенные в масштабах μs и μt.
- приращение функции и аргумента, построенные в масштабах μs и μt. и
и  откуда
откуда ,
,  .
. , но
, но  ;
; . (1.8)
. (1.8)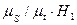 - представляет собой только масштабы построения, то отрезок
- представляет собой только масштабы построения, то отрезок  .
. или, сравнивая с (1.8),
или, сравнивая с (1.8), . (1.9)
. (1.9)
 представляет собой среднюю скорость движения на участке 1 2. Полученные точки 1’, 2’, 3’, 4’, 5’, 6’ соединяем плавной кривой. Получим график скорости точки С
представляет собой среднюю скорость движения на участке 1 2. Полученные точки 1’, 2’, 3’, 4’, 5’, 6’ соединяем плавной кривой. Получим график скорости точки С  .
. - среднее ускорение на первом участке, отрезок
- среднее ускорение на первом участке, отрезок  - среднее ускорение на втором участке и так далее. Соединяя точки 1'', 2'', 3'', 4'', 5'', 6'' плавной линией, получаем диаграмму ускорения точки С
- среднее ускорение на втором участке и так далее. Соединяя точки 1'', 2'', 3'', 4'', 5'', 6'' плавной линией, получаем диаграмму ускорения точки С 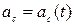 .
. . (1.10)
. (1.10) ;
; ;
;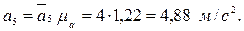
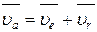 . (1.11)
. (1.11)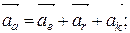 (1.12)
(1.12)

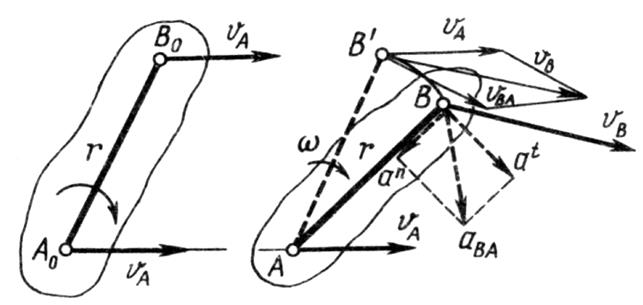 Рисунок 1.20
Рисунок 1.20 относительно тела К, необходимо повернуть на 90о по направлению угловой скорости -
относительно тела К, необходимо повернуть на 90о по направлению угловой скорости -  .
.
 ,
, 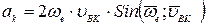 , (1.13)
, (1.13) , (1.14)
, (1.14) (1.15)
(1.15) (l 1 – длина звена ОА); вектор υА перпендикулярен ОА и направлен по угловой скорости ω1. Для определения абсолютной скорости точки В в соответствии с теоремой 1 рассмотрим движение звена АВ как сумму поступательного переносного движения вместе с полюсом – точкой А и относительного вращения вокруг полюса А.
(l 1 – длина звена ОА); вектор υА перпендикулярен ОА и направлен по угловой скорости ω1. Для определения абсолютной скорости точки В в соответствии с теоремой 1 рассмотрим движение звена АВ как сумму поступательного переносного движения вместе с полюсом – точкой А и относительного вращения вокруг полюса А.
 перпендикулярна звену О1В, а вектора
перпендикулярна звену О1В, а вектора  - звену АВ (в уравнении (1.14) векторы, известные по модулю и направлению, подчеркнуты дважды, а векторы, у которых известна только линия действия, - один раз). При графическом решении уравнения (1.14) на чертеже выбирают начало отсчета – точку р υ (рисунок 1.21, б), откладывают от нее в направлении скорости υА отрезок рυa. Длину отрезка рυa выбирают из условия удобства дальнейших построений: отрезок рυa определяет масштабный коэффициент плана скоростей:
- звену АВ (в уравнении (1.14) векторы, известные по модулю и направлению, подчеркнуты дважды, а векторы, у которых известна только линия действия, - один раз). При графическом решении уравнения (1.14) на чертеже выбирают начало отсчета – точку р υ (рисунок 1.21, б), откладывают от нее в направлении скорости υА отрезок рυa. Длину отрезка рυa выбирают из условия удобства дальнейших построений: отрезок рυa определяет масштабный коэффициент плана скоростей: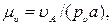 (1.16)
(1.16)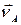 , проводим линию действия вектора
, проводим линию действия вектора  перпендикулярную АВ, а через начальную точку р υ – линию действия вектора
перпендикулярную АВ, а через начальную точку р υ – линию действия вектора 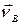 перпендикулярную О1В. Точка b пересечения этих линий определяет отрезок р υ b, изображающий вектор
перпендикулярную О1В. Точка b пересечения этих линий определяет отрезок р υ b, изображающий вектор 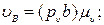

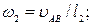
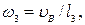
 и
и  переносим мысленно с плана скоростей на план механизма в точку В и видим, что звено 2 вращается относительно точки А по часовой стрелке, а звено 3 относительно точки О1 – против часовой стрелки (рисунок 1.21, а).
переносим мысленно с плана скоростей на план механизма в точку В и видим, что звено 2 вращается относительно точки А по часовой стрелке, а звено 3 относительно точки О1 – против часовой стрелки (рисунок 1.21, а).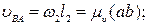
 тогда абсолютная скорость точки С звена 2, м/с:
тогда абсолютная скорость точки С звена 2, м/с:

 равно векторной сумме нормального ускорения
равно векторной сумме нормального ускорения  , направленного от точки А к точке О, и касательного
, направленного от точки А к точке О, и касательного 
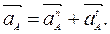 ( 1.17)
( 1.17) и
и  векторы
векторы  и
и  ; вектор
; вектор  плана изображает полное ускорение а А. Масштабный коэффициент плана ускорений [(м/с2)/мм]:
плана изображает полное ускорение а А. Масштабный коэффициент плана ускорений [(м/с2)/мм]:
 . (1.18)
. (1.18) по модулю равен
по модулю равен  и как центростремительный направлен по прямой АВ от точки В к центру относительного вращения – точке А. Вектор касательного ускорения
и как центростремительный направлен по прямой АВ от точки В к центру относительного вращения – точке А. Вектор касательного ускорения  перпендикулярен прямой АВ. В уравнении (1.18) двумя чертами подчеркнуты ускорения, известные по модулю и направлению, а одной чертой – когда известна лишь линия действия. Так как ни модуль, ни линия действия вектора
перпендикулярен прямой АВ. В уравнении (1.18) двумя чертами подчеркнуты ускорения, известные по модулю и направлению, а одной чертой – когда известна лишь линия действия. Так как ни модуль, ни линия действия вектора  неизвестны, а у вектора
неизвестны, а у вектора  , (1.19)
, (1.19) параллельно ВО1; а линия действия вектора
параллельно ВО1; а линия действия вектора 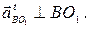
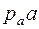 представляет собой первое слагаемое векторного уравнения (1.18) - ускорение аА. От точки а откладывают отрезок
представляет собой первое слагаемое векторного уравнения (1.18) - ускорение аА. От точки а откладывают отрезок 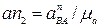 , изображающий вектор
, изображающий вектор 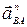 , который направлен параллельно звену ВА от точки В к точке А (так как звено 2 вращается относительно точки А, а вектор
, который направлен параллельно звену ВА от точки В к точке А (так как звено 2 вращается относительно точки А, а вектор  .
. находится искомая точка b; отрезок
находится искомая точка b; отрезок 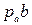 изображает вектор
изображает вектор  и
и  изображают соответственно векторы
изображают соответственно векторы 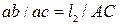 .
. подобен
подобен  ;
;  .
. ;
;  .
.


