Задача 3.12. К кривошипу 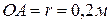 , равномерно вращающемуся в плоскости рисунка вокруг точки
, равномерно вращающемуся в плоскости рисунка вокруг точки  с угловой скоростью
с угловой скоростью  , прикреплен шатун
, прикреплен шатун 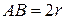 , соединенный с коромыслом
, соединенный с коромыслом 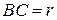 . Определить ускорение
. Определить ускорение  точки
точки  шатуна, угловые скорости
шатуна, угловые скорости 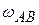 ,
,  и угловые ускорения
и угловые ускорения 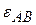 ,
, 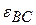 шатуна
шатуна  и коромысла
и коромысла  .
.
Решение. Начнем с определения скоростей. Шатун  совершает плоскопараллельное движение. Движение точки
совершает плоскопараллельное движение. Движение точки  можно легко определить. Поэтому за полюс примем точку
можно легко определить. Поэтому за полюс примем точку  и по исходным данным определим скорость и ускорение точки А шатуна. Так как точку
и по исходным данным определим скорость и ускорение точки А шатуна. Так как точку  принадлежит и равномерно вращающемуся кривошипу
принадлежит и равномерно вращающемуся кривошипу  , то по (2.16)
, то по (2.16) 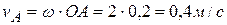 . Вектор
. Вектор  перпендикулярен к
перпендикулярен к  и направлен в сторону вращения кривошипа. По формулам (2.17) и (2.18) при
и направлен в сторону вращения кривошипа. По формулам (2.17) и (2.18) при 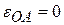 :
: 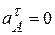 ,
, 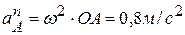 . Вектор нормального ускорения
. Вектор нормального ускорения 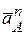 направлен от точки
направлен от точки  к точке О. Точка
к точке О. Точка  принадлежит вращающемуся коромыслу
принадлежит вращающемуся коромыслу  и шатуну
и шатуну  одновременно. Следовательно, траектория точки В известна. Точки В движется по окружности радиуса ВС. Поэтому вектор скорости
одновременно. Следовательно, траектория точки В известна. Точки В движется по окружности радиуса ВС. Поэтому вектор скорости  перпендикулярен к
перпендикулярен к  и направлен так, как показано на рисунке 2 к задаче. Последнее следует из теоремы о проекциях скоростей. По этой же теореме находится и величина
и направлен так, как показано на рисунке 2 к задаче. Последнее следует из теоремы о проекциях скоростей. По этой же теореме находится и величина  . Проецируя векторы
. Проецируя векторы 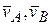 на ось
на ось 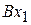 , получим:
, получим: 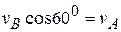 . Или
. Или 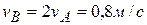 .
.
Чтобы найти 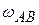 ,
,  построим мгновенный центр скоростей
построим мгновенный центр скоростей  шатуна АВ. Из треугольника
шатуна АВ. Из треугольника 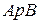 видно, что
видно, что 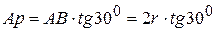 . Или
. Или 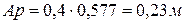 .
.
Тогда 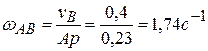 ,
, 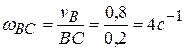 .
.
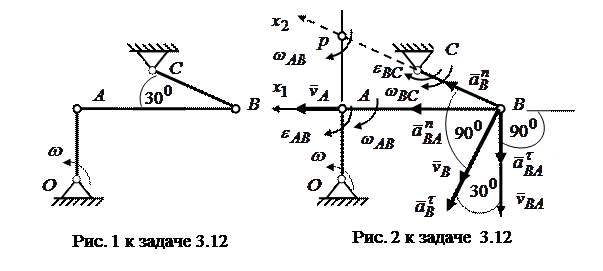
Переходим к определению ускорений. Векторы нормальных ускорений отдельных точек тел, совершающих вращательное движение, направлены к оси вращения. То есть их направления всегда известны, если известна ось вращения. В данной задаче оси вращения проходят через точки 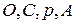 перпендикулярно плоскости рисунка. Оси, проходящие через точки
перпендикулярно плоскости рисунка. Оси, проходящие через точки 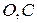 , - неподвижны, а две другие – подвижные, «мгновенные» оси. Векторы касательных ускорений отдельных точек вращающихся тел направлены по касательным к их траекториям, но часто бывает не известно в какую сторону. Если направления векторов линейных скоростей точек уже известны, то неизвестные векторы касательных ускорений будем направлять в ту же сторону. Это соответствует предположению об ускоренном движении точек. Угловые ускорения вращающихся тел, связаны с соответствующими касательными ускорениями, направления их согласованы. С учетом сказанного, на рис.2 показаны векторы касательных ускорений точек
, - неподвижны, а две другие – подвижные, «мгновенные» оси. Векторы касательных ускорений отдельных точек вращающихся тел направлены по касательным к их траекториям, но часто бывает не известно в какую сторону. Если направления векторов линейных скоростей точек уже известны, то неизвестные векторы касательных ускорений будем направлять в ту же сторону. Это соответствует предположению об ускоренном движении точек. Угловые ускорения вращающихся тел, связаны с соответствующими касательными ускорениями, направления их согласованы. С учетом сказанного, на рис.2 показаны векторы касательных ускорений точек 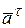 и угловых ускорений тел
и угловых ускорений тел  .
.
Учитывая, что точки  и
и  описывают окружности радиуса
описывают окружности радиуса  и
и  соответственно, запишем векторное уравнение (3.20):
соответственно, запишем векторное уравнение (3.20):
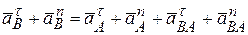 (*)
(*)
где 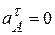 ,
, 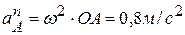 ,
, 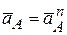 ,
, 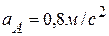 ,
, 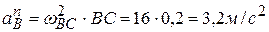 ,
, 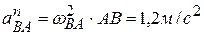 .Все векторы ускорений показаны на рисунке 2 к задаче. Модули векторов
.Все векторы ускорений показаны на рисунке 2 к задаче. Модули векторов 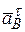 ,
, 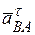 пока неизвестны.
пока неизвестны.
Спроектируем обе части векторного уравнения (*) сначала на ось Вх1 (направление ВА), затем на ось Вх2 (направление ВС):
 ,
, 
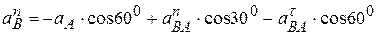 .
.
Решая совместно эти уравнения, получим:
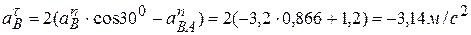 .
.
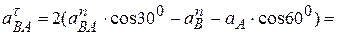
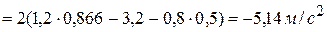 .
.
Математически знак минус указывает на то, что векторы 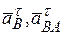 , показанные на рисунке 2, в действительности направлены в обратную сторону, и их истинные направления, удовлетворяющие уравнению (*), не совпадают с направлениями соответствующих векторов линейных скоростей
, показанные на рисунке 2, в действительности направлены в обратную сторону, и их истинные направления, удовлетворяющие уравнению (*), не совпадают с направлениями соответствующих векторов линейных скоростей 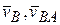 , которые уже были определены. С механической стороны не совпадение направлений соответствующих векторов линейных скоростей и ускорений означает, что точка
, которые уже были определены. С механической стороны не совпадение направлений соответствующих векторов линейных скоростей и ускорений означает, что точка  в данный момент совершает мгновенно замедленное движение.
в данный момент совершает мгновенно замедленное движение.
Вычислим, наконец, модуль ускорения точки  и угловые ускорения шатуна
и угловые ускорения шатуна  и коромысла
и коромысла 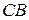 -
- 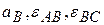 .
.
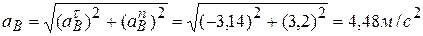 ,
, 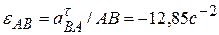 ,
, 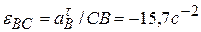
Знак (–) вобоих случаях связан с полученными знаками для соответствующих проекций векторов 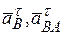 и указывает на то, что вращение шатуна АВ икоромысла ВС из рассматриваемого положения является замедленным. Другими словами, истинные направления криволинейных стрелок
и указывает на то, что вращение шатуна АВ икоромысла ВС из рассматриваемого положения является замедленным. Другими словами, истинные направления криволинейных стрелок 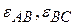 противоположно тому, что показано на рисунке 2 к задаче. Ответ:
противоположно тому, что показано на рисунке 2 к задаче. Ответ: 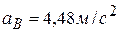 ,
, 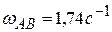 ,
,
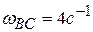 ,
, 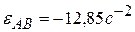 ,
, 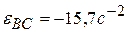 .
.
Задача 3.13. Груз 3 движется согласно закону 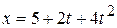 . Определить скорости и ускорения точек
. Определить скорости и ускорения точек  ,
,  ,
, 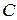 подвижного блока в момент времени
подвижного блока в момент времени 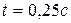 , если радиус подвижного блока
, если радиус подвижного блока 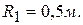
Решение: Груз 3 движется поступательно вниз. Его скорость 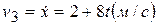 . При
. При 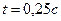 ;
; 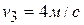 , ускорение
, ускорение 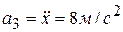 . Блок 1 движется плоскопараллельно. Так как левая часть нити неподвижна, то точка
. Блок 1 движется плоскопараллельно. Так как левая часть нити неподвижна, то точка  имеет скорость
имеет скорость 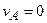 . Следовательно, точка
. Следовательно, точка 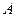 - мгновенный центр скоростей (МЦС) блока 1. Так как проскальзывание нити по блоку 1 отсутствует, значение скорости в точке
- мгновенный центр скоростей (МЦС) блока 1. Так как проскальзывание нити по блоку 1 отсутствует, значение скорости в точке  равно значению скорости груза 3, то есть
равно значению скорости груза 3, то есть 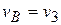 . Угловая скорость блока 1 при
. Угловая скорость блока 1 при 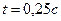 равна
равна 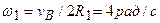 . Найдем скорости точек
. Найдем скорости точек 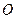 и
и 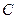 подвижного блока:
подвижного блока: 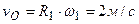 ;
; 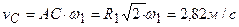 .
.
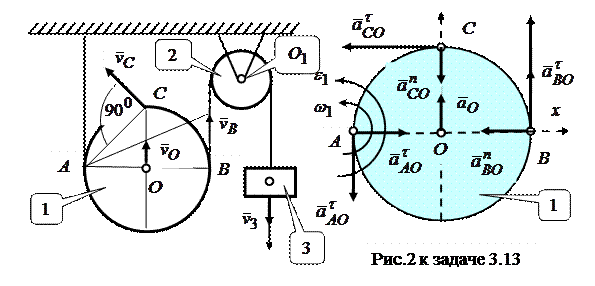
Определим ускорения точек А, В, С плоской фигуры. Касательное ускорение точки 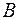 равно ускорению груза 3:
равно ускорению груза 3: 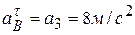 . Так как
. Так как 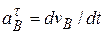 , то
, то 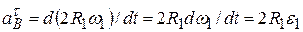 и
и 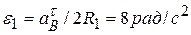 ;
; 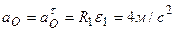 . Значение
. Значение 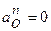 , так как точка О движется прямолинейно. Итак, модуль и направление ускорения точки
, так как точка О движется прямолинейно. Итак, модуль и направление ускорения точки 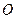 известны, поэтому будем считать данную точку полюсом. По (3.25) найдем векторы ускорений точек
известны, поэтому будем считать данную точку полюсом. По (3.25) найдем векторы ускорений точек  ,
,  и
и 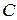 :
:
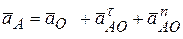 ;
; 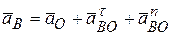 ;
; 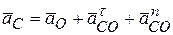
Спроецируем эти векторные равенства на оси О 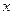 , О
, О 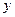 .
.
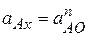 ;
; 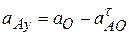 ;
; 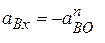 ;
; 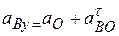 ;
;
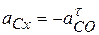 ;
; 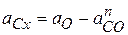 ,
,
где 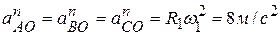 ,
, 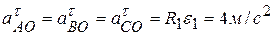 .
.
Тогда 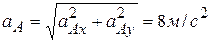 ;
; 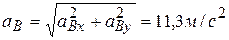 ;
;
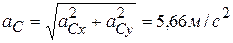 .
.
Отметим, что 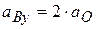 . Это значит, что величины ускорений точек нити (или груза 3) в два раза больше величины ускорения точки О. Ответ:
. Это значит, что величины ускорений точек нити (или груза 3) в два раза больше величины ускорения точки О. Ответ: 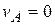 ;
; 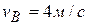 ;
; 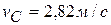 ;
; 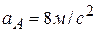 ;
; 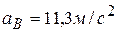 ;
; 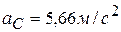 .
.
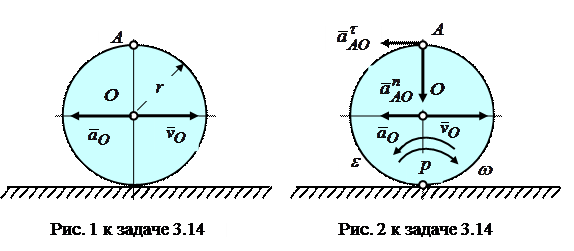
Задача 3.14. Диск радиуса 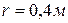 , совершающий плоскопараллельное движение, катится без скольжения по горизонтальной плоскости (рис. 1 к задаче 3.14). Центр диска движется равнозамедленно с ускорением
, совершающий плоскопараллельное движение, катится без скольжения по горизонтальной плоскости (рис. 1 к задаче 3.14). Центр диска движется равнозамедленно с ускорением 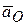 , модуль которого
, модуль которого 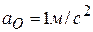 . Определить вектор полного ускорения
. Определить вектор полного ускорения  точки
точки  диска в тот момент времени
диска в тот момент времени  , когда скорость центра
, когда скорость центра 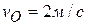 .
.
Решение. Для определения вектора ускорения  точки
точки  воспользуемся формулой (3.25), приняв за полюс центр диска точку
воспользуемся формулой (3.25), приняв за полюс центр диска точку  , скорость и ускорение которой известны.
, скорость и ускорение которой известны.
 +
+ 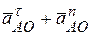 . (*)
. (*)
Здесь 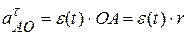 ,
, 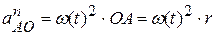 . Найдем угловую скорость и угловое ускорение диска, учитывая, что точка
. Найдем угловую скорость и угловое ускорение диска, учитывая, что точка  является мгновенным центром скоростей.
является мгновенным центром скоростей. 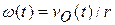 , и для момента времени
, и для момента времени  , когда
, когда 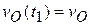 , имеем следующее значение угловой скорости:
, имеем следующее значение угловой скорости:
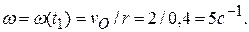 (**)
(**)
Направление 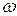 соответствует направлению вектора скорости
соответствует направлению вектора скорости  и показано дуговой стрелкой на рис.2 к задаче 3.14.
и показано дуговой стрелкой на рис.2 к задаче 3.14.
Замечание: по условию задачи центр диска движется замедленно. Другими словами его скорость меняется с течением времени. То есть надо считать, что величина скорости есть функция времени 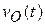 . Следовательно, и угловая скорость диска
. Следовательно, и угловая скорость диска 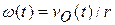 есть функция времени. Но в момент времени
есть функция времени. Но в момент времени  по условию задачи
по условию задачи 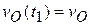 и
и 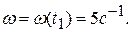
Угловое ускорение диска в любой момент времени вычисляется по формуле 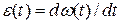 . Продифференцируем по времени
. Продифференцируем по времени 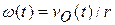 с учетом того, что расстояние от точки О до МЦС в любой момент времени равно
с учетом того, что расстояние от точки О до МЦС в любой момент времени равно 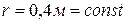 . Тогда
. Тогда 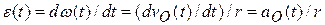 . По условию задачи центр диска движется равнозамедленно, то есть с постоянным ускорением (замедлением)
. По условию задачи центр диска движется равнозамедленно, то есть с постоянным ускорением (замедлением) 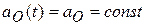 . Тогда в любой момент времени, в том числе и при
. Тогда в любой момент времени, в том числе и при  , для модуля углового ускорения имеем:
, для модуля углового ускорения имеем: 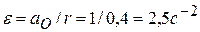 . Следовательно, и
. Следовательно, и 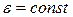 . Оно имеет одно и то же значение для любого момента времени. Направление
. Оно имеет одно и то же значение для любого момента времени. Направление  соответствует направлению вектора ускорения
соответствует направлению вектора ускорения 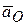 и показано дуговой стрелкой на рис.2 к задаче 3.14. Направления
и показано дуговой стрелкой на рис.2 к задаче 3.14. Направления 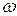 и
и  не совпадают, поэтому движение диска замедленное.
не совпадают, поэтому движение диска замедленное.
Теперь для момента времени  можно вычислить
можно вычислить 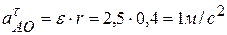 ,
, 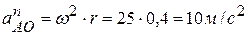 . Вектор касательного ускорения
. Вектор касательного ускорения 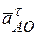 приложен к точке
приложен к точке  и направлен по направлению дуговой стрелки
и направлен по направлению дуговой стрелки  (Рис.2,3 к примеру). Векторнормального ускорения
(Рис.2,3 к примеру). Векторнормального ускорения 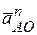 приложен к точке
приложен к точке  и направлен к полюсу
и направлен к полюсу  .
.
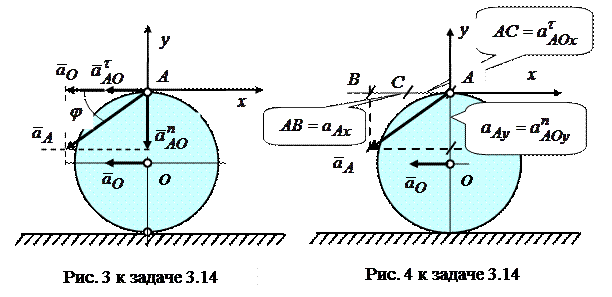
1.Геометрическая интерпретация векторного равенства (*) показана на рис.3 к примеру. Вектор ускорения 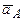 точки
точки  получается сложение по правилу параллелограмма двух взаимно перпендикулярных векторов
получается сложение по правилу параллелограмма двух взаимно перпендикулярных векторов 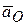 +
+ 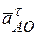 и
и 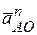 (рис.3). Эти векторы взаимно перпендикулярны, параллелограмм превращается в прямоугольник. Поэтому величину (модуль) вектора
(рис.3). Эти векторы взаимно перпендикулярны, параллелограмм превращается в прямоугольник. Поэтому величину (модуль) вектора  можно найти по теореме Пифагора:
можно найти по теореме Пифагора:
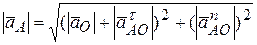 =
= 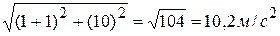 .
.
Угол наклона вектора  , как видно по рисунку, определится из уравнения
, как видно по рисунку, определится из уравнения 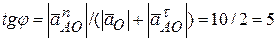 . Отсюда
. Отсюда 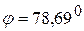 . 2. Для определения вектора
. 2. Для определения вектора  можно воспользоваться методом проекций. Спроецируем уравнение (*) на оси координат
можно воспользоваться методом проекций. Спроецируем уравнение (*) на оси координат 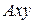 (см. рис. 3 и 4). Получим:
(см. рис. 3 и 4). Получим: 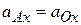 +
+ 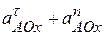 ,
, 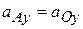 +
+ 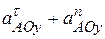 . Здесь
. Здесь 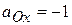 ,
, 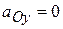 ,
, 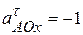 ,
, 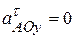 ,
, 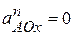 ,
, 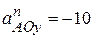 . Тогда
. Тогда 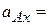
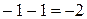 ,
, 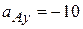 . Модуль вектора вычисляется обычным способом:
. Модуль вектора вычисляется обычным способом: 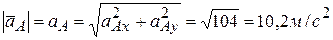 . Направление вектора полного ускорения
. Направление вектора полного ускорения  определяется в данном случае по знакам его проекций на оси координат, а для модуля угла
определяется в данном случае по знакам его проекций на оси координат, а для модуля угла  имеем уравнение
имеем уравнение 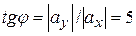 . Отсюда
. Отсюда 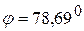 , что полностью совпадает с полученным ранее значением. Ответ:
, что полностью совпадает с полученным ранее значением. Ответ: 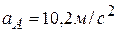 ,
, 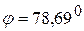 .
.
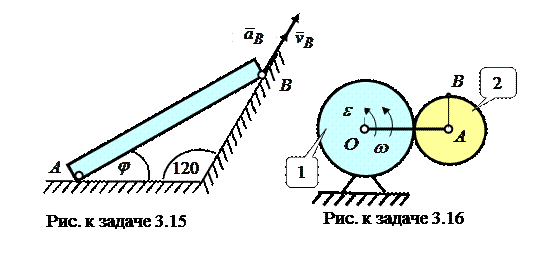
Задача 3.15. Концы бруса  , движущегося в вертикальной плоскости, скользят по горизонтальной и наклонной плоскостям (рис. к задаче 3.15). В момент времени, когда
, движущегося в вертикальной плоскости, скользят по горизонтальной и наклонной плоскостям (рис. к задаче 3.15). В момент времени, когда 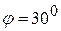 , величина скорости
, величина скорости 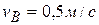 и величина ускорения
и величина ускорения 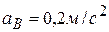 . Определить в данный момент времени величины скорости
. Определить в данный момент времени величины скорости 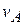 и ускорения
и ускорения 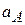 конца
конца  бруса, угловую скорость бруса
бруса, угловую скорость бруса 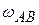 и угловое ускорение
и угловое ускорение 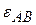 , если
, если  . Ответ:
. Ответ: 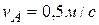 ,
, 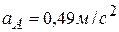 ,
, 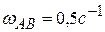 ,
, 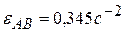 .
.
Задача 3.16. По неподвижной шестерне 1 радиуса 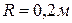 обкатывается шестерня 2 радиуса
обкатывается шестерня 2 радиуса 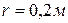 , насаженная на кривошип
, насаженная на кривошип  . Кривошип
. Кривошип  вращается относительно неподвижной оси, проходящей перпендикулярно плоскости рисунка через точку
вращается относительно неподвижной оси, проходящей перпендикулярно плоскости рисунка через точку  , и имеет в данный момент времени угловую скорость
, и имеет в данный момент времени угловую скорость  и угловое ускорение
и угловое ускорение 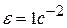 . Определить в данный момент времени угловую скорость
. Определить в данный момент времени угловую скорость  , угловое ускорение
, угловое ускорение 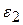 второй шестерни и величину ускорения
второй шестерни и величину ускорения 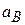 точки
точки  , если радиус
, если радиус  перпендикулярен оси кривошипа
перпендикулярен оси кривошипа  . Ответ:
. Ответ: 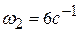 ,
, 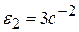 ,
, 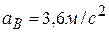 .
.
Задача 3.17. Стержень  длиной
длиной 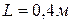 движется в плоскости чертежа. В некоторый момент времени точки
движется в плоскости чертежа. В некоторый момент времени точки  и
и  имели ускорения, модули которых
имели ускорения, модули которых 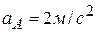 ,
, 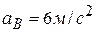 . Определить угловое ускорение стержня
. Определить угловое ускорение стержня 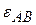 , если в данный момент времени угол
, если в данный момент времени угол 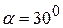 . Ответ:
. Ответ: 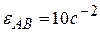 .
.
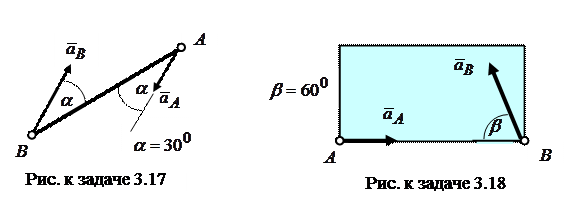
Задача 3.18. Тело в форме прямоугольника находится в плоскопараллельном движении. Найти в показанный на рисунке момент времени его угловую скорость 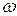 , если модули ускорений
, если модули ускорений  ,
, 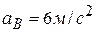 . Расстояние
. Расстояние  , угол
, угол 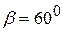 . Ответ:
. Ответ: 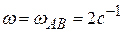 .
.
Задача 3.19. Определить величину ускорения 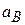 ползуна
ползуна  и угловое ускорение
и угловое ускорение 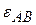 шатуна
шатуна  кривошипно-шатунного механизма в показанном на рисунке положении, если угловое ускорение кривошипа в данный момент времени
кривошипно-шатунного механизма в показанном на рисунке положении, если угловое ускорение кривошипа в данный момент времени 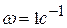 . Длины звеньев
. Длины звеньев 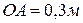 ,
, 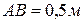 . Ответ:
. Ответ: 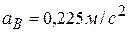 ,
, 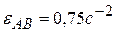 .
.
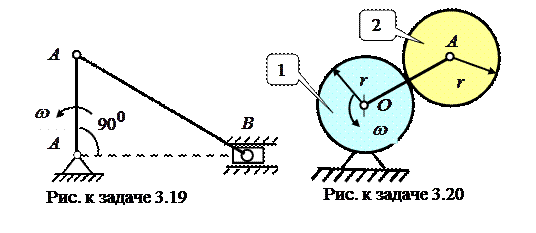
Задача 3.20. Кривошип  планетарного механизма вращается с постоянной угловой скоростью
планетарного механизма вращается с постоянной угловой скоростью 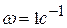 относительно оси, проходящей перпендикулярно к плоскости рисунка через центр
относительно оси, проходящей перпендикулярно к плоскости рисунка через центр  неподвижного колеса
неподвижного колеса  . Определить модуль ускорения точки
. Определить модуль ускорения точки  , являющейся мгновенным центром скоростей подвижного колеса
, являющейся мгновенным центром скоростей подвижного колеса  , если радиусы колес
, если радиусы колес 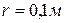 . Ответ:
. Ответ: 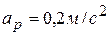 .
.
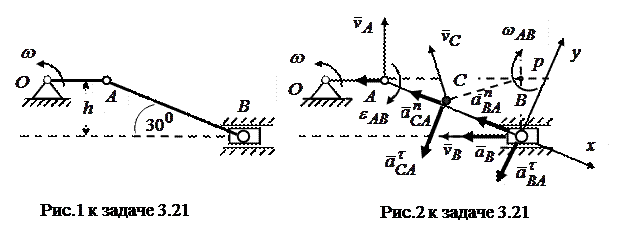
Задача 3.21. Кривошип  кривошипно-шатунного механизма вращается с постоянной угловой скоростью
кривошипно-шатунного механизма вращается с постоянной угловой скоростью  . В показанном на рисунке положении механизма определить угловую скорость
. В показанном на рисунке положении механизма определить угловую скорость 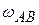 и угловое ускорение
и угловое ускорение 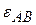 шатуна АВ, модули скоростей и ускорений точек
шатуна АВ, модули скоростей и ускорений точек  , если
, если 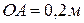 ,
, 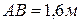 ,
, 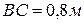 ,
, 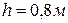 . Ответ:
. Ответ: 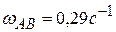 ,
,  ,
, 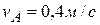 ,
, 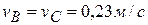 ,
, 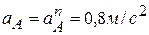 ,
, 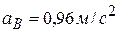 ,
, 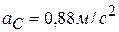 .
.
Замечание: На рис.1 к задаче приведена исходная схема механизма. На рис. 2 к задаче приведена расчетная схема, которая сопровождает вычисления. Это некоторая «подсказка» к решению. Рекомендуется при решении задачи на первом этапе разобраться со скоростями, а векторы ускорений с рисунка убрать. На втором этапе определяются ускорения. При этом векторы скоростей с рисунка надо убрать, чтобы не загромождать рисунок.
Вопросы для самоконтроля к главе 3.
1.Какое движение твердого тела называется плоскопараллельным или плоским?
2. Запишите уравнения плоскопараллельно движения твердого тела.
3. Из каких простейших движений твердого тела математически «складывается» плоскопараллельное движение?
4. Сформулируйте и поясните теорему о геометрическом сложении скоростей точек плоской фигуры.
5. Запишите уравнения метода проекций для определения скорости произвольной точки плоской фигуры.
6. Какая точка плоской фигуры называется полюсом?
7. Зависят ли угловая скорость и угловое ускорение плоской фигуры от выбора полюса?
8. Как вычисляется скорость произвольной точки плоской фигуры при вращении фигуры относительно полюса в плоскопараллельном движении?
9. Сформулируйте теорему о проекциях векторов скоростей двух точек плоской фигуры на ось, проходящую через эти точки.
10. Что называется мгновенным центром скоростей плоской фигуры
11. Как определяется мгновенный центр скоростей плоской фигуры при известных направлениях векторов скоростей двух точек плоской фигуры?
12. Покажите положение мгновенного центра скоростей для известных Вам частных случаев движения плоской фигуры.
13. Как вычисляется скорость произвольной точки плоской фигуры в плоскопараллельном движении при известном положении мгновенного центра скоростей?
14. Сформулируйте теорему о геометрическом сложении векторов ускорений при плоскопараллельном движении плоской фигуры. Из каких векторов состоит в общем случае вектор ускорения произвольной точки плоской фигуры?
15. Как направлены и как вычисляются величины касательной и нормальной составляющих вектора ускорения произвольной точки, возникающего от вращения плоской фигуры относительно полюса?
16. Запишите уравнения метода проекций для определения ускорения произвольной точки плоской фигуры.
17. Какая точка называется мгновенным центром ускорений плоской фигуры?
18. Как вычисляется ускорение произвольной точки плоской фигуры при известном мгновенном центре ускорений?



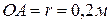 , равномерно вращающемуся в плоскости рисунка вокруг точки
, равномерно вращающемуся в плоскости рисунка вокруг точки  с угловой скоростью
с угловой скоростью  , прикреплен шатун
, прикреплен шатун 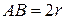 , соединенный с коромыслом
, соединенный с коромыслом 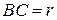 . Определить ускорение
. Определить ускорение  точки
точки  шатуна, угловые скорости
шатуна, угловые скорости 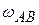 ,
,  и угловые ускорения
и угловые ускорения 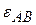 ,
, 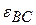 шатуна
шатуна  и коромысла
и коромысла  .
. можно легко определить. Поэтому за полюс примем точку
можно легко определить. Поэтому за полюс примем точку  , то по (2.16)
, то по (2.16) 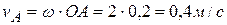 . Вектор
. Вектор  перпендикулярен к
перпендикулярен к 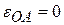 :
: 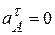 ,
, 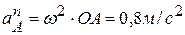 . Вектор нормального ускорения
. Вектор нормального ускорения 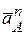 направлен от точки
направлен от точки  перпендикулярен к
перпендикулярен к  . Проецируя векторы
. Проецируя векторы 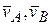 на ось
на ось 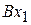 , получим:
, получим: 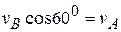 . Или
. Или 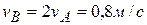 .
. шатуна АВ. Из треугольника
шатуна АВ. Из треугольника 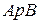 видно, что
видно, что 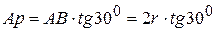 . Или
. Или 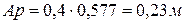 .
.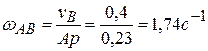 ,
, 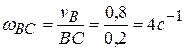 .
.
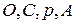 перпендикулярно плоскости рисунка. Оси, проходящие через точки
перпендикулярно плоскости рисунка. Оси, проходящие через точки 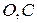 , - неподвижны, а две другие – подвижные, «мгновенные» оси. Векторы касательных ускорений отдельных точек вращающихся тел направлены по касательным к их траекториям, но часто бывает не известно в какую сторону. Если направления векторов линейных скоростей точек уже известны, то неизвестные векторы касательных ускорений будем направлять в ту же сторону. Это соответствует предположению об ускоренном движении точек. Угловые ускорения вращающихся тел, связаны с соответствующими касательными ускорениями, направления их согласованы. С учетом сказанного, на рис.2 показаны векторы касательных ускорений точек
, - неподвижны, а две другие – подвижные, «мгновенные» оси. Векторы касательных ускорений отдельных точек вращающихся тел направлены по касательным к их траекториям, но часто бывает не известно в какую сторону. Если направления векторов линейных скоростей точек уже известны, то неизвестные векторы касательных ускорений будем направлять в ту же сторону. Это соответствует предположению об ускоренном движении точек. Угловые ускорения вращающихся тел, связаны с соответствующими касательными ускорениями, направления их согласованы. С учетом сказанного, на рис.2 показаны векторы касательных ускорений точек 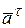 и угловых ускорений тел
и угловых ускорений тел  .
.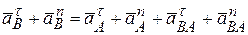 (*)
(*)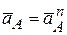 ,
, 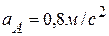 ,
, 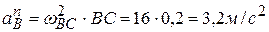 ,
, 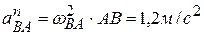 .Все векторы ускорений показаны на рисунке 2 к задаче. Модули векторов
.Все векторы ускорений показаны на рисунке 2 к задаче. Модули векторов 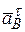 ,
, 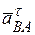 пока неизвестны.
пока неизвестны. ,
, 
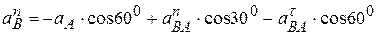 .
.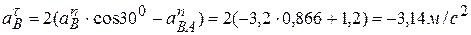 .
.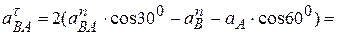
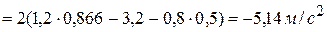 .
.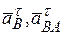 , показанные на рисунке 2, в действительности направлены в обратную сторону, и их истинные направления, удовлетворяющие уравнению (*), не совпадают с направлениями соответствующих векторов линейных скоростей
, показанные на рисунке 2, в действительности направлены в обратную сторону, и их истинные направления, удовлетворяющие уравнению (*), не совпадают с направлениями соответствующих векторов линейных скоростей 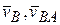 , которые уже были определены. С механической стороны не совпадение направлений соответствующих векторов линейных скоростей и ускорений означает, что точка
, которые уже были определены. С механической стороны не совпадение направлений соответствующих векторов линейных скоростей и ускорений означает, что точка 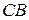 -
- 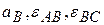 .
.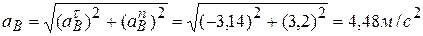 ,
, 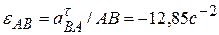 ,
, 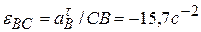
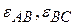 противоположно тому, что показано на рисунке 2 к задаче. Ответ:
противоположно тому, что показано на рисунке 2 к задаче. Ответ: 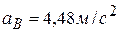 ,
, 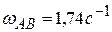 ,
,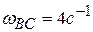 ,
, 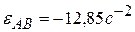 ,
, 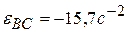 .
.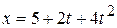 . Определить скорости и ускорения точек
. Определить скорости и ускорения точек 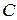 подвижного блока в момент времени
подвижного блока в момент времени 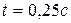 , если радиус подвижного блока
, если радиус подвижного блока 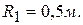
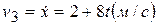 . При
. При 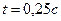 ;
; 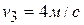 , ускорение
, ускорение 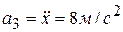 . Блок 1 движется плоскопараллельно. Так как левая часть нити неподвижна, то точка
. Блок 1 движется плоскопараллельно. Так как левая часть нити неподвижна, то точка 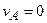 . Следовательно, точка
. Следовательно, точка 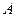 - мгновенный центр скоростей (МЦС) блока 1. Так как проскальзывание нити по блоку 1 отсутствует, значение скорости в точке
- мгновенный центр скоростей (МЦС) блока 1. Так как проскальзывание нити по блоку 1 отсутствует, значение скорости в точке 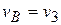 . Угловая скорость блока 1 при
. Угловая скорость блока 1 при 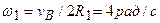 . Найдем скорости точек
. Найдем скорости точек 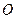 и
и 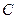 подвижного блока:
подвижного блока: 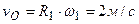 ;
; 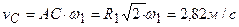 .
.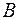 равно ускорению груза 3:
равно ускорению груза 3: 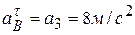 . Так как
. Так как 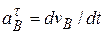 , то
, то 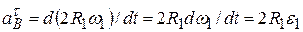 и
и 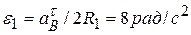 ;
; 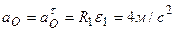 . Значение
. Значение 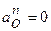 , так как точка О движется прямолинейно. Итак, модуль и направление ускорения точки
, так как точка О движется прямолинейно. Итак, модуль и направление ускорения точки 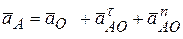 ;
; 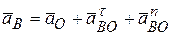 ;
; 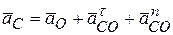
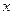 , О
, О 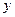 .
.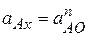 ;
; 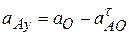 ;
; 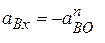 ;
; 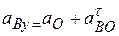 ;
;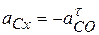 ;
; 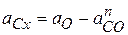 ,
,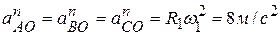 ,
, 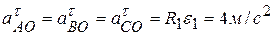 .
.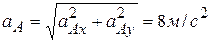 ;
; 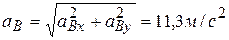 ;
;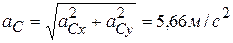 .
.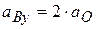 . Это значит, что величины ускорений точек нити (или груза 3) в два раза больше величины ускорения точки О. Ответ:
. Это значит, что величины ускорений точек нити (или груза 3) в два раза больше величины ускорения точки О. Ответ: 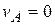 ;
; 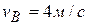 ;
; 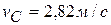 ;
; 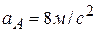 ;
; 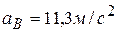 ;
; 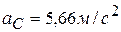 .
.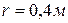 , совершающий плоскопараллельное движение, катится без скольжения по горизонтальной плоскости (рис. 1 к задаче 3.14). Центр диска движется равнозамедленно с ускорением
, совершающий плоскопараллельное движение, катится без скольжения по горизонтальной плоскости (рис. 1 к задаче 3.14). Центр диска движется равнозамедленно с ускорением 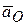 , модуль которого
, модуль которого 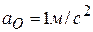 . Определить вектор полного ускорения
. Определить вектор полного ускорения  точки
точки  , когда скорость центра
, когда скорость центра 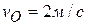 .
.
 +
+ 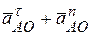 . (*)
. (*)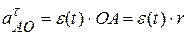 ,
, 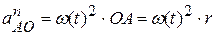 . Найдем угловую скорость и угловое ускорение диска, учитывая, что точка
. Найдем угловую скорость и угловое ускорение диска, учитывая, что точка 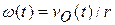 , и для момента времени
, и для момента времени 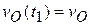 , имеем следующее значение угловой скорости:
, имеем следующее значение угловой скорости: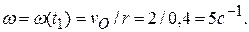 (**)
(**)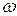 соответствует направлению вектора скорости
соответствует направлению вектора скорости  и показано дуговой стрелкой на рис.2 к задаче 3.14.
и показано дуговой стрелкой на рис.2 к задаче 3.14.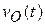 . Следовательно, и угловая скорость диска
. Следовательно, и угловая скорость диска 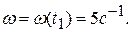
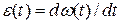 . Продифференцируем по времени
. Продифференцируем по времени 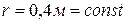 . Тогда
. Тогда 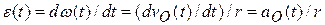 . По условию задачи центр диска движется равнозамедленно, то есть с постоянным ускорением (замедлением)
. По условию задачи центр диска движется равнозамедленно, то есть с постоянным ускорением (замедлением) 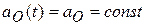 . Тогда в любой момент времени, в том числе и при
. Тогда в любой момент времени, в том числе и при 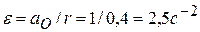 . Следовательно, и
. Следовательно, и 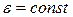 . Оно имеет одно и то же значение для любого момента времени. Направление
. Оно имеет одно и то же значение для любого момента времени. Направление 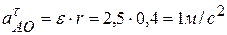 ,
, 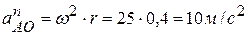 . Вектор касательного ускорения
. Вектор касательного ускорения 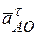 приложен к точке
приложен к точке 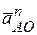 приложен к точке
приложен к точке 
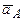 точки
точки 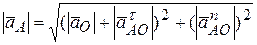 =
= 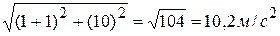 .
.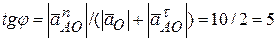 . Отсюда
. Отсюда 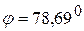 . 2. Для определения вектора
. 2. Для определения вектора 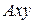 (см. рис. 3 и 4). Получим:
(см. рис. 3 и 4). Получим: 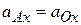 +
+ 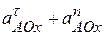 ,
, 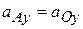 +
+ 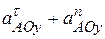 . Здесь
. Здесь 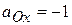 ,
, 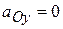 ,
, 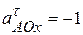 ,
, 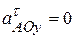 ,
, 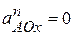 ,
, 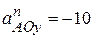 . Тогда
. Тогда 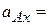
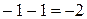 ,
, 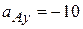 . Модуль вектора вычисляется обычным способом:
. Модуль вектора вычисляется обычным способом: 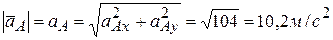 . Направление вектора полного ускорения
. Направление вектора полного ускорения  имеем уравнение
имеем уравнение 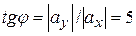 . Отсюда
. Отсюда 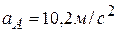 ,
, 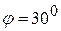 , величина скорости
, величина скорости 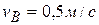 и величина ускорения
и величина ускорения 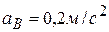 . Определить в данный момент времени величины скорости
. Определить в данный момент времени величины скорости 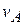 и ускорения
и ускорения 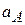 конца
конца  . Ответ:
. Ответ: 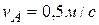 ,
, 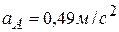 ,
, 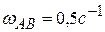 ,
, 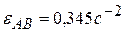 .
.
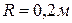 обкатывается шестерня 2 радиуса
обкатывается шестерня 2 радиуса 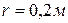 , насаженная на кривошип
, насаженная на кривошип  и угловое ускорение
и угловое ускорение 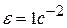 . Определить в данный момент времени угловую скорость
. Определить в данный момент времени угловую скорость  , угловое ускорение
, угловое ускорение 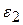 второй шестерни и величину ускорения
второй шестерни и величину ускорения 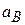 точки
точки 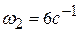 ,
, 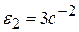 ,
, 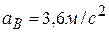 .
.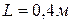 движется в плоскости чертежа. В некоторый момент времени точки
движется в плоскости чертежа. В некоторый момент времени точки 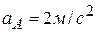 ,
, 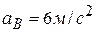 . Определить угловое ускорение стержня
. Определить угловое ускорение стержня 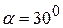 . Ответ:
. Ответ: 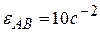 .
.
 ,
, 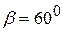 . Ответ:
. Ответ: 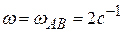 .
.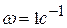 . Длины звеньев
. Длины звеньев 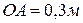 ,
, 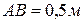 . Ответ:
. Ответ: 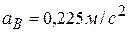 ,
, 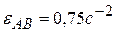 .
.
 . Определить модуль ускорения точки
. Определить модуль ускорения точки  , если радиусы колес
, если радиусы колес 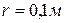 . Ответ:
. Ответ: 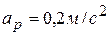 .
. , если
, если 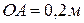 ,
, 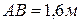 ,
, 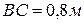 ,
, 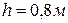 . Ответ:
. Ответ: 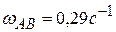 ,
,  ,
, 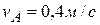 ,
, 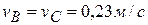 ,
, 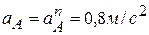 ,
, 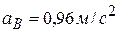 ,
, 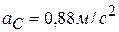 .
.



