
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Статически неопределимые балки при изгибе ⇐ ПредыдущаяСтр 8 из 8
Как уже ранее мы отмечали, в случае действия нагрузки на балку в одной плоскости, минимальное число связей, обеспечивающее неподвижность балки по отношению к основанию, равно трем. Эти три связи являются абсолютно необходимыми. Удаление хотя бы одной из таких связей превращает балку в геометрически изменяемую систему (механизм). Поскольку для плоской системы сил можно составить три уравнения равновесия, то балки, закрепленные тремя связями, являются статически определимыми. Исключение составляют многопролетные шарнирные балки, которые могут быть статически определимыми и при числе внешних связей больше трех (об этом выше уже говорилось). Очень часто, для обеспечения требуемой прочности и жесткости балки, оказывается необходимым увеличить число опорных закреплений, т.е. ввести некоторые «лишние» связи. В балках с «лишними» связями все реакции нельзя определить только из уравнений равновесия. Такие балки будут статически неопределимыми. Число «лишних» неизвестных определяет степень статической неопределимости системы. Для раскрытия статической неопределимости балок разработано несколько методов. Рассмотрим один из них – с использованием метода Клебша для определения деформации балки. Порядок расчета таких балок заключается в следующем: 1. Составляем обычные три уравнения статики для всей балки (как при определении опорных реакций). 2. Для всех участков балки с учетом правил метода Клебша записываем дифференциальные уравнения (5.20) и интегрируем их. 3. Из условий закрепления балки составляем дополнительные уравнения, которые с уравнениями статики дают необходимую систему алгебраических уравнений для определения всех опорных реакций и констант После определения всех опорных реакций, расчет балки на прочность и жесткость ведется обычным (как показано выше) путем.
1. Уравнения статики:
2. Уравнения деформации балки. Здесь один участок а) в) с) 3. Рассмотрим закрепление балки: Сечение А (заделка), при Сечение В, опора, при
Решаем уравнения (7)¸(9) и находим § 5.12. Энергия деформации
От
От Как показано выше в разделе 3 (3.16), при действии В объеме тела
В объеме всего бруса, площадью сечения
Здесь учтено, что Итак, при плоском изгибе
В случае чистого изгиба, когда
|
|||||||
|
Последнее изменение этой страницы: 2016-12-13; просмотров: 508; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.143.9.115 (0.006 с.) |
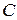 и
и 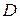 .
.
 и
и  . Задача однажды статически неопределима.
. Задача однажды статически неопределима.

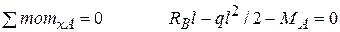 (7)
(7) (8)
(8)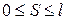 лев. часть
лев. часть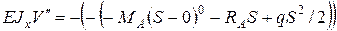
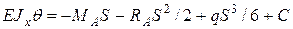
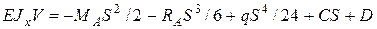
 . Подставим в уравнение в), найдем
. Подставим в уравнение в), найдем  . Сечение А, при
. Сечение А, при  и
и  . Подставим в с) найдем
. Подставим в с) найдем 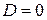 .
.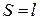 ,
,  (9)
(9) ,
,  в точках сечения возникают
в точках сечения возникают и
и  . (10)
. (10)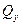 возникают
возникают  , определяемый формулой Журавского и
, определяемый формулой Журавского и  -по закону Гука при сдвиге.
-по закону Гука при сдвиге. и
и  удельная энергия деформации
удельная энергия деформации  , аналогично от
, аналогично от  ,
,  . В общем случае
. В общем случае  . Анализ показал, что
. Анализ показал, что  много меньше
много меньше  , поэтому
, поэтому  .
. энергия деформации
энергия деформации 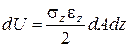 . Подставляя сюда (10), получим
. Подставляя сюда (10), получим .
. и длиной l, полную энергию U найдем интегрированием по
и длиной l, полную энергию U найдем интегрированием по  .
. и
и 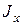
 по
по 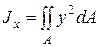 .
. . (5.21)
. (5.21) по l и балка постоянного сечения
по l и балка постоянного сечения  , получим из (5.21):
, получим из (5.21): . (5.22)
. (5.22)


