Элементы теории принятия решений. Таблицы соответствий. Алгоритмы поиска решений

Поиск решений в пространстве состояний сводится к определению последовательности операторов, отображающих начальные состояния в целевые. Причем если такая последовательность операторов не одна и задан критерий оптимальности, то поиск сводится к нахождению оптимальной последовательности, т. е. последовательности операторов, обеспечивающей оптимум заданного критерия оптимальности. Методы поиска решений в пространстве состояний удобно рассмотреть, используя дерево (граф) состояний. На дереве состояний поиск решения сводится к определению пути (оптимального, если задан критерий оптимальности) от корня дерева к целевой вершине, т.е. к вершине, соответствующей целевому состоянию. Поиск решения можно наглядно проиллюстрировать на дереве состояний, когда начальное состояние одно. Поэтому сначала рассмотрим задачи, определяемые тройкой (S_o, F, G), в которой множество S_o начальных состояний состоит из одного элемента. Напомним, что в указанной тройке F — множество операторов, отображающих пространство состояний в себя; G — множество целевых состояний.

Для построения дерева состояния следует, используя операторы из F, применимые к корню дерева (начальному состоянию), построить вершины 1-го уровня. Затем, используя операторы из F, применимые к вершинам 1-го уровня, построить вершины 2-го уровня и т. д. Процесс применения операторов к какой-либо вершине дерева для построения всех ее дочерних вершин называется раскрытием вершины. Поэтому операторы преобразования мира (операторы из F) интерпретируются как правила раскрытия вершин. Применение правил раскрытия к начальной вершине порождает совокупность дочерних вершин. Каждая из них соответствует некоторому состоянию мира, в которое он может перейти из начального состояния. Дуги, связывающие начальную вершину с дочерней, идентифицируются как соответствующие операторы преобразования. Для всех дочерних вершин производится проверка, не являются ли они целевыми, т. е. не соответствуют ли целевым состояниям. Если целевая вершина не обнаружена, то выполняется следующий этап порождения вершин путем применения правил раскрытия к каждой вершине, порожденной на предыдущем этапе. Полученное множество вершин также анализируется на присутствие целевой вершины. Процедура продолжается до обнаружения целевой вершины.

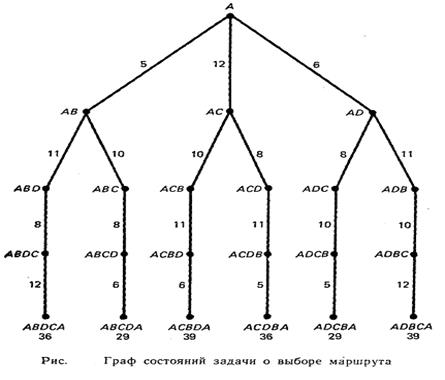
Рассмотрим, процедуру построения графа состояний на примере выбора маршрута транспортным роботом, который должен, выйдя из склада (пункта А), обойти обрабатывающие центры (пункты В, С, D) и вернуться в склад. Запрещается, чтобы робот побывал в каком-либо из обрабатывающих центров более одного раза. Схема маршрутов и расстояние между пунктами представлена на рис. 5.1

Условимся: состояние в этой задаче обозначать словом (набором букв), образованным из букв, соответствующих наименованию пунктов, пройденных к текущему моменту, и расположенных в том порядке, в каком были пройдены соответствующие пункты.

 

Рис. 5.1 Граф состояний о выборе маршрута

 

Тогда, очевидно, начальным будет состояние А, а целевыми будут состояния, которые обозначаются словами, начинающимися и кончающимися буквой А и включающими по одному разу наименования всех остальных пунктов. Состояния, кроме целевых, которые описываются словами, содержащими повторяющиеся буквы, являются недопустимыми.

Операторы (или правила раскрытия) в данном примере соответствуют выбору того или иного маршрута. Так как из каждого пункта можно попасть в любые три другие пункта, то множество состоит из 12 операторов. Причем применимыми к любому данному состоянию являются не более трех операторов.

На графе состояний этой задачи начальной вершине (корню дерева) соответствует состояние А. Корень дерева порождает три дочерние вершины, соответствующие состояниям АВ, АС и AD. Каждая из вершин, порожденных корнем, порождает по две вершины и каждая из вершин 2-го и 3-го уровней — по одной. На дугах указаны расстояния, которые проходит робот при переходе из одного состояния в другое. На концевых вершинах, соответствующих целевым состояниям, указаны кроме состояний расстояния, которые проходит робот из начального состояния в заданное целевое состояние.

Поиск решения имеет итеративный характер, причем число итераций и вершин, раскрытых до нахождения целевой вершины, существенно зависит от порядка (последовательности), в котором раскрывались вершины. Порядок раскрытия вершин принято называть стратегией поиска.

Можно выделить два основных типа стратегий поиска: «слепой» перебор и упорядоченный перебор вершин-кандидатов на раскрытие. Слепой перебор характеризуется тем, что расположение целевых вершин или их близость не влияют на порядок раскрытия. Существует несколько алгоритмов слепого перебора. Рассмотрим три наиболее типичных: алгоритм полного перебора, алгоритм равных-цен, алгоритм перебора в глубину.

Алгоритм полного перебора. Вершины раскрываются в том порядке, в котором они были порождены. Первой раскрывается начальная вершина. Проверяется, нет ли среди порожденных вершин целевой. Если есть, то поиск заканчивается. Если нет, то раскрывается первая из порожденных вершин и проверяется наличие целевых вершин. Затем раскрывается вторая из порожденных вершин и т. д.

Для структурированной записи алгоритмов поиска в пространстве состояний введем понятия списков открытых (ОТК) и закрытых (ЗКР) вершин. Список закрытых вершин — это список, где размещаются идентификаторы раскрытых вершин и идентификатор вершины, которую предстоит раскрыть в данный момент. Вершины из списка ЗКР, кроме последней, раскрывать нельзя. Список открытых вершин — это список, где размещаются вершины, которые могут и должны быть раскрыты. Стратегии поиска различаются правилами размещения вершин в списке ОТК и выбора очередной вершины для раскрытия.

В структурированном виде алгоритм полного перебора можно представить следующим образом.

1. Поместить начальную вершину в список ОТК.

2. Если список ОТК пуст, то подать сигнал о неудаче поиска, в ином случае перейти к следующему шагу.

3. Взять первую вершину из списка ОТК и перенести ее в список ЗКР; присвоить вершине идентификатор v.

4. Раскрыть вершину v. Поместить все дочерние неповторяющиеся (т. е. не встречающиеся в списке ЗКР) вершины в конец списка ОТК и построить указатели, ведущие от них к вершине v. Если вершина v не имеет дочерних вершин или имеет только повторяющиеся дочерние вершины, то перейти к шагу 2.

5. Проверить, не является ли одна из дочерних вершин v целевой. Если является, то выдать решение; в ином случае перейти к шагу 2.

В этом алгоритме предполагается, что начальная вершина (корень) не может быть целевой. Алгоритм, безусловно, позволяет найти оптимальное (минимальное по числу дуг) решение. Например, использование этого алгоритма для решения задачи о выборе маршрута (с минимальным расстоянием) по существу сводится к построению графа состояний. Имея этот граф и сравнивая расстояния различных маршрутов, ведущих к целевым состояниям, можно выбрать оптимальные маршруты. Как следует из графа состояний, таких маршрутов два — маршруты, ведущие к целевым состояниям ABCDA и ADCBA.

Алгоритм равных цен. Пусть каждой дуге поставлена в соответствие некоторая функция стоимости с_ij. Требуется найти путь минимальной стоимости. Раскрытие вершин осуществляется в порядке возрастания их стоимости. Обозначим g(v) — стоимость раскрытия некоторой вершины v и опишем алгоритм равных цен.

1. Поместить начальную вершину s_о в список ОТК.

Положить g(s_o)=0.

2. Если список ОТК пуст, то подать сигнал о неудаче поиска; в ином случае перейти к следующему шагу.

3.Взять из списка ОТК ту вершину, для которой величина g(v) имеет наименьшее значение, и поместить ее в список ЗКР. Присвоить этой вершине идентификатор v (если вершин с минимальной стоимостью несколько, то можно выбрать любую из них).

4. Если v есть целевая вершина, то выдать решающий путь; в ином случае перейти к следующему шагу.

5. Раскрыть вершину v. Для каждой дочерней вершины v_i вычислить стоимость g (v_i) по формуле g (v_i) = g(v)+ c(v, v_i). Поместить эти вершины вместе с соответствующими им g(v_i) в список ОТК и построить указатели, идущие от них к вершине v. Если вершина v не имеет дочерних вершин, то сразу перейти к шагу 2.

6. Перейти к шагу 2.

Алгоритм равных цен является обобщением алгоритма полного перебора и сводится к нему при условии, что стоимости раскрытия всех вершин равны. При применении этого алгоритма для решения задачи о выборе маршрута раскрывается меньшее число вершин. Граф решения приведен на рис.29, где на дугах указаны «стоимости» с (v, v_i), а на вершинах кроме обозначения состояния — значение функции g(v_i,), а также (в скобках) порядковый номер, в котором раскрываются вершины.

Алгоритм перебора в глубину. Определим глубину вершины числом, равным номеру ее уровня. При методе перебора в глубину всегда раскрывается та из вершин, которая имеет наибольшую глубину. Так как несколько вершин могут иметь одинаковую наибольшую глубину, предполагается, что имеется правило выбора одной из них. Кроме того, обычно по тем или иным соображениям задается граничная глубина; вершины, имеющие глубину, равную граничной, не раскрываются. Таким образом, метод перебора в глубину можно определить как метод перебора, при котором всегда раскрывается та из вершин, которая имеет наибольшую глубину, меньшую граничной.

Рис. 5.2 Граф решения задачи о выборе маршрута при использовании алгоритма равных цен

Рассмотрим алгоритм перебора в глубину в структурированном виде.

1. Поместить начальную вершину в список ОТК.

2. Если список ОТК пуст, то выдается сообщение о неудаче, в ином случае перейти к шагу 3.

3. Взять первую вершину из списка ОТК и перенести в список ЗКР. Этой вершине присвоить идентификатор v.

4. Если глубина вершины v равна граничной глубине, то перейти к 2, в ином случае — к 5.

5. Раскрыть вершину v. Поместить все дочерние вершины в начало списка ОТК и построить указатели, идущие от них к вершине v. Если v не имеет дочерних вершин, то перейти к шагу 2.

6. Если одна из этих вершин целевая, то на выход выдать решение, получаемое путем просмотра назад в соответствии с указателями, в ином случае перейти к шагу 2.

Один из возможных графов решения задачи выбора маршрута с помощью алгоритма перебора в глубину приведен на рис.5.3. При применении этого алгоритма решение зависит от стратегии упорядочения вершин в списке ОТК. В приведенном решении найден неоптимальный маршрут.

Во всех рассмотренных алгоритмах перебора предполагается, что начальная вершина только одна. Если начальных вершин несколько, то эти алгоритмы изменяются только на шаге 1: на шаге 1 в список ОТК помещаются все начальные вершины.

Достоинством методов слепого перебора является, во-первых, простота алгоритмической реализации, во-вторых, обязательность получения решения, если оно существует. Недостатком этих методов является резкое возрастание числа вершин, которые необходимо раскрыть в процессе поиска решения, с увеличением размерности задачи. Это существенно сужает круг практических задач, которые могут быть решены методами слепого перебора.

Рис. 5.3. Граф решения задачи о выборе маршрута при использовании алгоритма перебора в глубину

Алгоритмы упорядоченного перебора. Для большинства практических задач удается сформулировать эмпирические правила, позволяющие уменьшить объем перебора. Эти правила используют специфическую информацию о решаемой задаче, формируемую на основе опыта, интуиции и здравого смысла исследователя.

Информацию такого рода часто называют эвристической, а основанные на ней алгоритмы — эвристическими.

Основная идея эвристических алгоритмов заключается в упорядочении списка открытых вершин в соответствии с некоторой мерой, оценивающей «перспективность» вершины или пути, на котором находится данная вершина. Такую меру называют оценочной функцией. Для очередного раскрытия из списка ОТК выбирается вершина, имеющая минимальное значение оценочной функции. После каждого шага раскрытия производится переупорядочение вершин в списке в соответствии со значениями оценочной функции. Процедуру такого типа называют алгоритмом упорядоченного перебора.

Существуют различные идеологии построения оценочных функций. Рассмотрим наиболее распространенную

Пусть g(v) — стоимость кратчайшего (оптимального) пути из любой начальной вершины s_o S_o до некоторой вершины v. Стоимость кратчайшего пути из вершины и до ближайшей целевой вершины

g_o G обозначим h (v). Функция f(v) = g(v)+h(v), очевидно, выражает стоимость кратчайшего (оптимального) пути из начальной вершины в целевую при условии, что он проходит через вершину v.

Введем в рассмотрение следующие оценочные функ­ции: g (v) — оценка стоимости кратчайшего пути из начальной вершины в вершину и; h(v) — оценка стоимости кратчайшего пути из вершины v до ближайшей целевой. Тогда функция

F (v) = g(v)+h(v) (5.2)

будет оценочной функцией функции f(v), т. е. она является оценкой стоимости кратчайшего пути из начальной вершины в целевую при условии, что он проходит через вершину v.

В качестве оценочной функции g(v) естественно выбрать действительную стоимость пути от начальной вершины к вершине v найденного алгоритмом перебора к данному моменту. Заметим, что если граф состояний не имеет структуру дерева, то значение g(v) может меняться в процессе раскрытия вершин. Поясним это свойство на примере (рис. 5.4). Пусть на шаге 1 поиска раскрыта вершина s0 и порождены вершины v₁ и v₂ со значениями стоимостей g(v₁)=3 и g(v₂)=7 (рис. 5.4, а). На шаге 2 раскрывается вершина v₁ и порождается вершина v₃ и снова вершина v₂, причем из v₁ в v₂ ведет путь стоимостью g(v₁) = 3 (рис. 5.4,6). Очевидно, стоимость «кратчайшего» пути из s₀ в v₂ будет g(v₂)=6. Как следует из определения и приведенного примера, g(v) ≥ g(v). Эта оценочная функция легко вычисляется в процессе работы алгоритма.

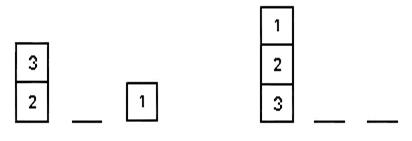
Рис. 5.4 Граф состояний, не имеющий структуру дерева

Определение оценочной функции h(v) является более сложной задачей. При ее построении опираются на любую эвристическую информацию о решаемой задаче, поэтому h(v) называют эвристической функцией. Очевидно, если h(v)=0, то алгоритм перебора сводится к алгоритму равных цен, что соответствует полному отсутствию эвристической информации.

Не существует каких-либо конструктивных рекомендаций к способам определения этой функции, поэтому рассмотрим ее смысл на примере. Конкретизируем задачу преобразования сцен (задачу о манипуляции предметами) следующим образом. Три пронумерованных кубика располагаются на трех площадках. Манипуляционный робот может перемещать с одной площадки на другую по одному кубику. Кубики могут устанавливаться друг на друга. Для перемещения разрешается брать только верхний кубик. Заданы начальное и целевое расположения кубиков. Задача заключается в определении плана перемещения кубиков, позволяющего за минимальное число шагов (шаг — одно перемещение кубика) перейти от начального расположения к целевому. На рис. 5.5 представлены целевое и на­чальное расположения кубиков на площадках.

В качестве эвристической функции h(v) примем сумму числа кубиков, расположенных не на своем месте, и общее число кубиков, препятствующих установлению каждого из них на свое место.

Начальное состояние Целевое состояние

Рис. 5.5. Расположение кубиков на площадке

 

Препятствующими считаются кубики, расположенные сверху какого-либо кубика, который нужно переставить, и кубики, которые занимают «чужие» места в целевой конфигурации, т. е. места, в которые должны быть установлены кубики, расположенные не на своем месте.

Граф решения задачи с помощью алгоритма упорядоченного перебора при указанной эвристической функции приведен на рис. 5.6 Для удобства вершины пронумерованы. Эвристическая функция вершины 1 равна h₁(v)=7, так как не на своем месте расположены два кубика (2 и 3). Места, которые они должны занять, заняты другими кубиками и над кубиком 2 расположены два кубика, а над кубиком 3 — один (h(1)=2 + 2 + + 2+1=7). Поэтому оценочная функция f (1) = g(1) + + h(1)=8. Аналогично можно подсчитать значения оценочной функции на других вершинах 1-го уровня.

Среди вершин 1-го уровня наименьшее значение функции f имеет вершина 3. Поэтому на шаге 2 раскрывается эта вершина. При этом повторяющиеся вершины не строятся и значения функции f таких вершин сохраняются, так как функция g с каждым шагом возрастает, а функция h не изменяется. На шаге 3 возникает задача выбора вершины, которую нужно раскрыть на этом шаге, так как на трех вершинах (5, 6 и 4) оценочная функция f принимает одинаковые минимальные значения. Условимся, что при одинаковых значениях f предпочтение отдается тем вершинам, у которых меньше h. Вершины 5 и 6 имеют одинаковые значения f и h Граф решения, приведенный на рис. 33, соответствует случаю, когда эти вершины упорядочены так, что сначала раскрывается вершина 5.

Рассмотрим некоторые свойства эвристических алгоритмов упорядоченного перебора. Алгоритм называют гарантирующим или допустимым, если для произвольного графа состояний он заканчивает работу построением оптимального пути.

Можно показать, что алгоритм упорядоченного перебора, использующий оценочную функцию вида (29), является гарантирующим, если для всех вершин v выполняется условие

h(v) ≤ h(v) и стоимости всех дуг превосходят некоторое положительное число.

Рис. 5.6. Граф решения задачи преобразования сцен.

 

 

Для сравнения эффективности алгоритмов перебора используется понятие эвристической силы. Пусть A₁ и А₂ — произвольные гарантирующие алгоритмы перебора, a f₁=g(v)+h₁(v) и f₂=g(v)+h₂(v) — используемые ими оценочные функции. Алгоритм А₁ называют эвристически более сильным, чем алгоритм A₂, если на всех вершинах, кроме целевой, выполняется неравенство h₁(v)>h₂(v). Эвристически более сильный алгоритм А₁ раскрывает меньшее число вершин при поиске минимального пути, чем алгоритм А₂. Обозначим В — множество гарантирующих алгоритмов, которые можно использовать для решения данной задачи. Алгоритм А* В называют оптимальным, если он не раскрывает большее число вершин, чем любой другой алгоритм А В.

Оптимальность в указанном смысле не является исчерпывающей характеристикой эффективности алгоритма, так как не учитывает сложность вычисления эвристической функции h(v). В большинстве практических задач более объективной характеристикой является оценка объема вычислений, необходимых для определения значений h(v) на всех шагах к целевой вершине.

ВОПРОСЫ ДЛЯ САМОПРОВЕРКИ:

1. Какова последовательность решения задачи поиска оптимальных режимов обработки?

2. Каковы наиболее эффективные процедуры, однозначно приводящие к результату при решении задачи?

3. Как используются таблицы соответствий для формализации технологических задач?