
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Раздел 1. Задачи и объекты математического моделирования в машиностроительном производствеСтр 1 из 10Следующая ⇒
В МАШИНОСТРОЕНИИ
УЧЕБНОЕ ПОСОБИЕ
Институты: Машиностроительно-технологический институт Институт управления производственными и инновационными программами
Специальности: 151001.65 – технология машиностроения 080502.65 – экономика и управление на предприятии машиностроения
Специализации: 151001.65-27 – технология, промышленный менеджмент и маркетинг в машиностроении 151001.65-01 – технология автоматизированного производства
Направления подготовки бакалавров: 150900.62 – технология, оборудование и автоматизация машиностроительных производств
080500.62 – менеджмент
Санкт-Петербург Издательство СЗТУ Утверждено редакционно-издательским советом университета
УДК 621.01 (07)
Математическое моделирование в машиностроении: учебно-методический комплекс/ сост.: А. Е. Вороненко, Л. В. Одинцова, – СПб: Изд-во СЗТУ, 2011 г. – 122 с.
Учебно-методический комплекс разработан в соответствии с государственными образовательными стандартами высшего профессионального образования. В дисциплине рассматриваются задачи и объекты математического моделирования, аппарат моделирования дискретных объектов и процессов, математическая статистика в моделировании процессов функционирования систем. Учебно-методический комплекс предназначен для студентов специальностей 151001.65 – технология машиностроения и 080502.65 – экономика и управление на предприятии машиностроения. Для специальности 080502.65 дисциплина имеет название «Математическое моделирование процессов в машиностроении».
Рассмотрено на заседании кафедры технологии машиностроения «12» марта 2011 г.; одобрено методической комиссией машиностроительно-технологического института «12» апреля 2011 г.
Рецензенты: кафедра технологии машиностроения (зав. кафедрой В. В. Максаров, д-р техн. наук, проф.); кафедра автоматизации производственных процессов (зав. кафедрой А. А. Сарвин, д-р техн. наук, проф.).
Составители: А. Е. Вороненко, канд. техн. наук, доц., Л. В. Одинцова, канд. техн. наук, доц.,
© Северо-Западный государственный заочный технический университет, 2011 © Вороненко А. Е., Одинцова Л.В., 2011
Предисловие
Дисциплина «Математическое моделирование в машиностроении» изучается студентами специальности 151001.65 – технология машиностроения, а дисциплина «Математическое моделирование процессов в машиностроении» студентами специальности 080502.65 – экономика и управление на предприятии машиностроения.
Целью изучения дисциплины является углубление и конкретизация знаний в области математического моделирования, без чего невозможно познание современной технологической и экономической базы знаний, а главное, её успешное использование с применением средств вычислительной техники. При изучении курса необходимо: - знать математический аппарат, позволяющий наиболее адекватно описать типовые технологические и экономические задачи; - уметь выбрать из освоенного арсенала необходимый математический аппарат и применить соответствующую методику его использования при решении упомянутых задач подготовки и управления производством; - владеть математическими методами и программными средствами, дающими возможность анализировать и моделировать устройства, процессы и явления из области будущей деятельности студентов как специалистов. Место дисциплины в учебном процессе:
Настоящая дисциплина базируется на знании основ технологии машиностроения, соответствующих разделов высшей математики и теории экономического анализа. В свою очередь, материалы курса должны использоваться в дальнейшем при изучении дисциплин «Технология получения изделий в машиностроении», «Автоматизация производственных процессов в машиностроении», «Применение ПЭВМ в отрасли», «САПР технологических процессов». Знания, полученные при изучении дисциплин «Информатика», являются базой для использования ЭВМ при освоении разделов дисциплины, посвященных моделированию процессов функционирования систем, принятию решений в условиях определённости при технологическом проектировании и управлении производством. Конспект лекции
ВВЕДЕНИЕ В настоящее время модели используются в различных сферах человеческой деятельности, особенно в сферах проектирования и управления, где особенными являются процессы принятия эффективных решений на основе получаемой информации. Моделирование сейчас широко применяется в процессе создания и исследования новых машин, новых технологических процессов и поиске их оптимальных вариантов; при решении экономических задач, при решении задач планирования и управления производством на различных уровнях. В связи с этим в подготовке специалистов машиностроительного профиля предусмотрена дисциплина «Математическое моделирование в машиностроении».
Изучая дисциплину, будущий специалист в области машиностроения готовится к использованию существующих моделей и методов, способствующих созданию эффективных технологий изготовления продукции и автоматизированному проектированию объектов и процессов производства.
Раздел 1. Задачи и объекты математического моделирования в машиностроительном производстве Моделирование является общепризнанным средством познания окружающей человека действительности. Это обусловлено тем, что опыты на реальных системах, будь то экономика страны, отдельная организация или система управления технологическим процессом слишком сложны и неэффективны. Моделирование позволяет исследовать суть сложных процессов и явлений с помощью экспериментов не с реальной системой, а с моделью. Известно, что для принятия разумного решения по организации работы системы не обязательно знание всех ее характеристик, достаточен анализ упрощенного, приближенного представления системы. С помощью моделирования при проектировании новых систем можно на самых ранних стадиях разработки исследовать свойства и параметры будущего изделия или технологического (производственного) процесса. В организационных системах моделирование становится основным инструментом сравнения различных вариантов управляющих решений и поиска наиболее эффективного из них как для ситуаций внутри цеха, организации, фирмы, так и на макроэкономическом уровне. С тех пор как компьютер стал использоваться для исследования сложных объектов и процессов, появились два направления, которые можно охарактеризовать как математическое моделирование и имитационное моделирование. Разнообразие изучаемых явлений порождает необходимость правильно выбирать подходящие математические модели и корректно их использовать. При этом богатые возможности компьютеров в области анимации и визуального представления результатов работы модели позволяют понять суть исследуемых объектов и процессов. Все это делает математическое моделирование серьезной созидательной деятельностью. Желаем успехов в освоении этого вида профессиональной подготовки. Раздел 2. Моделирование дискретных объектов и процессов Операции над множествами. Самого по себе понятия множества еще недостаточно – нужно определить способы конструирования новых множеств из уже имеющихся, то есть совершать операции над множествами. Обычно рассматриваются следующие операции: 1 Объединением множеств А и В называется множество, состоящее из всех тех элементов, которые принадлежат хотя бы одному из множеств А, В. Символически это записывается так
Аналогично определяется объединение произвольной совокупности множеств. В общем случае можно использовать обозначение È А, которое формулируется как объединение всех множеств А, принадлежащих совокупности М.
Пример. Сборочная единица представляет собой объединение некоторого множества Т-систем «деталь» СЕ = È ТСД 2 Пересечением множеств А и В называется множество, состоящее из всех тех и только тех элементов, которые одновременно принадлежат и А и В. Символически это записывается так
Аналогично определяется пересечение произвольного числа множеств.
А \ В = {C ê C Î А и C Ï В }
В отличие от двух предыдущих операций разность строго двухместна, т.е. определена только для двух множеств и не коммутативна: А \ В ¹ В \ А Симметричная разность множеств А и В это множество. стоящее из элементов, которые принадлежат хотя бы одному из множеств А и В, но без элементов, которые одновременно принадлежат множествам А и В. А Δ В= (А U B) \ (A ∩ B)= {X | (X Є A и Х ÏВ) или (ХÏ А и е Є В)} А В
Отношения Обычно широко используемое понятие «отношение» имеет вполне определенное математическое значение. Прямым произведением множеств А и В называется множество пар (а,в),таких что а Î А, в Î В. А*В:= {(а,в) | а Є А и в Є В} Для представления множеств в программах, реализуемых на ЭВМ, необходимо описать в терминах используемой системы программирования структуру данных, используемую при исследовании объектов. Предполагается, что в системе программирования доступны такие структуры данных, как массивы, записи и указатели. Таким образом, применительно к множествам определение представления подразумевает описание способа хранения информации о принадлежности элементов множеству и описание алгоритмов для вычисления объединения, пересечения и других операций. Выбор представления зависит от целого ряда факторов: особенностей представляемого объекта, вида и относительной частоты использования операций в конкретной задаче и т.д. Умение выбрать подходящее для конкретного случая представление является творческой задачей практического программирования. ВОПРОСЫ ДЛЯ САМОПРОВЕРКИ:
1. При каком условии множество может быть представлено характеристическим предикатом? 2. Перечислите основные операции над множествами? Элементы теории графов. Граф – это некоторая совокупность двух множеств V (точек) и E (линий), между элементами которых определено отношение инцидентности, причем каждый элемент е Î Е инцидентен ровно двум элементам v1,v2 Î V. Элементы множества V называются вершинами графа G, элементы множества Е – его ребрами. Графы удобно изображать в виде рисунков, состоящих из точек и линий, соединяющих некоторые из этих точек. Две вершины соединяются непрерывной линией тогда и только тогда, когда в графе G есть ребро с этими вершинами. В некоторых случаях инцидентные ребру вершины неравноправны, т.е. они рассматриваются в определенном порядке. Тогда каждому ребру можно приписать направление от первой из инцидентных вершин ко второй. Направленные ребра называют дугами, а граф в этом случае – ориентированным. Первая по порядку вершина, инцидентная ребру ориентированного графа, называется его началом, а вторая – концом. Ребро ориентированного графа выходит из начала и входит в конец. Вершины, соединенные ребром или дугой, называются смежными. Ребра, имеющие общую вершину, также называются смежными. Граф называется полным, если любые две его различные вершины соединены одним и только одним ребром. Различные ребра могут быть инцидентны одной и той же паре вершин, в этом случае ребра называются кратными, а сам граф часто называют мультиграфом.
При изображении ориентированного графа направления ребер отмечаются стрелками, примыкающими к их концам. Ориентированный граф тоже может иметь кратные ребра и петли, а также соединяющие одни и те же вершины ребра, идущие в противоположных направлениях.
Матрица смежности графа Матрица смежности – это квадратная матрица ½dij½, столбцам и строкам которой соответствуют вершины графа. Для неориентированного графа dij равно количеству ребер, инцидентных i-й и j- й вершинам, для ориентированного графа этот элемент матрицы смежности равен количеству ребер с началом в i-й вершине и концом в j- й. Таким образом, матрица смежности неориентированного графа симметрична (dij = dji), а ориентированного не обязательно. Матрица смежности рассмотренных выше графов приведена в табл.3.2, 3.3. Таблица 3.2 Таблица 3.3 Степени вершин графа Локальной степенью (или просто степенью) вершин графа называется количество ребер, инцидентных вершине. Если задана матрица инцидентности, то для каждой j -й вершины r(vj) = S eij, а для матрицы смежности r(vj) = S dij.
Для вершин ориентированного графа определяются две локальные степени: r1(v) - число ребер с началом в вершине v, или, иначе, количество выходящих ребер, и r2(v) - количество входящих в v ребер. Так как каждое ребро ориентированного графа имеет одно начало и один конец, суммы r1(v) и r2(v) равны количеству ребер графа и равны между собой. Маршрутом в графе называется такая конечная последовательность ребер (е0,е1,…,ек), что каждые два соседние ребра имеют общую инцидентную вершину, Одно и то же ребро может встречаться в маршруте несколько раз. Если начало и конец маршрута совпадают, то он называется циклическим. Циклом называется путь, в котором совпадают его начальная и конечная вершины. Простым циклом в графе называется цикл, не проходящий ни через одну из вершин графа более одного раза. Длиной цикла называется число ребер в этом цикле. Путем от вершины Неориентированный граф без циклов (т.е. без петель и кратных ребер) называется лесом. Любая часть леса является деревом. Любую вершину дерева можно отметить и назвать корнем. Если все ребра дерева ориентировать из корня, то получится ориентированный граф-дерево. В каждую вершину ориентированного граф-дерева входит только одно ребро (а выходить может несколько). Число вершин граф-дерева на единицу больше числа ребер (рис.2.1).
Рис. 3.1. Ориентированный граф-дерево 3.2.Моделирование технических систем с использованием теории графов.
Графы используются при анализе функционирования сложных систем. С отдельными элементами изучаемой системы удобно связывать вершины графа, а взаимодействие парных элементов изображать ребрами графа. Построенный таким образом граф называют структурным графом системы. При решении задач создания структуры размерных связей в заготовке модели в виде графов дают наиболее наглядное представление и возможность автоматизировать этот процесс с помощью ЭВМ. Примеры использования графов при решении задач размерного анализа и синтеза приведены на рис. 3.2, 3.3.
Рис. 3.2 Пример использования графов при решении задачи размерного анализа
Рис. 3.3 Пример использования графов при решении задачи размерного синтеза
Граф, изображенный на рис. 3.4 называется сетевым графиком строительства. В данном случае он составлен для строительства жилого дома. Задача: узнать наименьшую возможную продолжительность строительства. Вершины этого графа обозначают отдельные виды работ на стройке: Ориентация дуги
Около вершин графа указаны числа – продолжительность в днях соответствующей работы. Для решения задачи из всех путей ориентированного графа нужно выбрать путь, соединяющий вершины Замечание. Если сократить, например, время прокладки электросети с 40 до 10 дней, то время строительства не сократится на 30 дней. В этом случае критический путь станет таким: {(А 0, (А 0, А 10), А 10, (А 10, А 9), А 9, (А 9, А 6), А 6, (А 6, А 7), А 7, (А 7, А 12), А 12}. Общее время строительства составит 160 дней, т.е. срок сократится только на 10 дней. ВОПРОСЫ ДЛЯ САМОПРОВЕРКИ: 1. Какой граф называется ориентированным? 2. Что называется маршрутом в графе? 3. Является ли конструкторский граф ориентированным? 4. Что называется локальной степенью вершин графа?
Планирование эксперимента Под экспериментом будем понимать совокупность операций совершаемых над объектом исследования с целью получения информации об его свойствах. Эксперимент, в котором исследователь по своему усмотрению может изменять условия его проведения, называется активным экспериментом. Если исследователь не может самостоятельно изменять условия его проведения, а лишь регистрирует их, то это пассивный эксперимент. Важнейшей задачей методов обработки полученной в ходе эксперимента информации является задача построения математической модели изучаемого явления, процесса, объекта. Ее можно использовать и при анализе процесс ов и при проектировании объектов. Можно получить хорошо аппроксимирующую математическую модель, если целенаправленно применяется активный эксперимент. Другой задачей обработки полученной в ходе эксперимента информации является задача оптимизации, т.е. нахождения такой комбинации влияющих независимых переменных, при которой выбранный показатель оптимальности принимает экстремальное значение. Опыт – это отдельная экспериментальная часть. План эксперимента – совокупность данных определяющих число, условия и порядок проведения опытов. Планирование эксперимента – выбор плана эксперимента, удовлетворяющего заданным требованиям, совокупность действий направленных на разработку стратегии экспериментирования (от получения априорной информации до получения работоспособной математической модели или определения оптимальных условий). Это целенаправленное управление экспериментом, реализуемое в условиях неполного знания механизма изучаемого явления. В процессе измерений, последующей обработки данных, а также формализации результатов в виде математической модели, возникают погрешности, и теряется часть информации, содержащейся в исходных данных. Применение методов планирования эксперимента позволяет определить погрешность математической модели и судить о ее адекватности. Если точность модели оказывается недостаточной, то применение методов планирования эксперимента позволяет модернизировать математическую модель с проведением дополнительных опытов без потери предыдущей информации и с минимальными затратами. Цель планирования эксперимента – нахождение таких условий и правил проведения опытов, при которых удается получить надежную и достоверную информацию об объекте с наименьшей затратой труда, а также представить эту информацию в компактной и удобной форме с количественной оценкой точности. Итак, для получения математической модели изучаемого процесса необходимо проводить эксперимент. Количество опытов должно быть минимальным, но достаточным для адекватного отражения изучаемого процесса в создаваемой математической модели. С этой целью составляется план полного факторного эксперимента (ПФЭ). Количество опытов в плане составит 2n, где n - число независимых переменных (факторов). Для плана ПФЭ 22 число факторов равно двум (n =2) и число уровней фиксирования факторов также 2. Если заранее не известно аналитическое выражение функции отклика, то можно рассматривать не саму функцию, а ее разложение, например в степенной ряд в виде полинома
Y=В0 + B1Х1 + … + BnХn + В12Х1Х2 + … Вnn-1ХnХn-1 + В11Х12 + … + ВnnXn2 +….
Разложение в степенной ряд функции возможно в том случае, если сама функция является непрерывной и гладкой. На практике обычно ограничиваются числом членов степенного ряда и аппроксимируют функцию полиномом некоторой степени. Факторы могут иметь разные размерности (А, В, Вт, об/мин) и резко отличаться количественно. В теории планирования эксперимента используют кодирование факторов.
Рис. 4.16. Пространство кодированных факторов
Эта операция заключается в выборе нового масштаба для кодированных факторов (рис. 4.16), причем такого, чтобы минимальное значение кодированных факторов соответствовало “-1”, а максимальное значение “+1”, а также в переносе начала координат в точку с координатами Х1ср, Х2ср, …, Хnср
Текущее значение кодированного фактора
где Хi – именованное (абсолютное) значение фактора; xi – кодированное значение фактора; Xicp -Ximin =Ximax-Xicp - интервал варьирования фактора. Полное число возможных сочетаний значений n факторов (число опытов, а значит и число строк плана) N =22=4. Составляется план, в котором число столбцов факторов и их сочетаний равняется числу членов уравнения. Так для уравнения
План ПФЭ 22 для этого уравнения представляется в следующем виде.
Столбцы, обведенные утолщенной рамкой, образуют план эксперимента. Столбцы, не обведенные утолщенной рамкой, при проведении опытов носят вспомогательный характер. В первый столбец (i =0) во все четыре ячейки заносятся +1. Во второй столбец (i =1) заносятся единицы с чередующими знаками (начинаем с -1). В этом случае сумма элемента столбца равняется нулю. Третий столбец заполняем единицами с чередующимися через 2 элемента знаками. Сумма элементов также равняется нулю. Геометрическое отображение плана ПФЭ 22 с указанием номеров точек плана в факторном пространстве представлено на рис. 4.17. Точки плана располагаются в вершинах квадрата.
Рис. 4.17 Геометрическое отображение плана ПФЭ 22 в факторном пространстве Элементы столбцов, соответствующих произведениям факторов получаются путем перемножения элементов предыдущих столбцов. Такое правило позволяет гарантировать, что мы не пропустили ни одного возможного сочетания факторов в опытах и в то же время не будет повторений одинаковых сочетаний. Последние два столбца факторов, соответствующие квадратам факторов, состоят только из +1. Столбцы, обведенные утолщенной рамкой, образуют план эксперимента. Столбец х1х2, не обведенный утолщенной рамкой, при проведении опытов носит вспомогательный характер. Особенности плана ПФЭ 22: 1. Различных столбцов в таблице получилось лишь четыре. Столбцы, соответствующие квадратам факторов неотличимы от столбца х 0 - это общий результат для плана ПФЭ 2n. Это не позволяет определить отдельно коэффициенты при квадратах факторов. Поэтому планы ПФЭ 2n называют планами первого порядка. Для определения коэффициентов при квадратах факторов используют планы второго порядка. В дальнейшем в планах ПФЭ 2n столбцы квадратов факторов изображаться не будут. 2. Число различных столбцов равняется числу различных сочетаний факторов, то есть числу строк плана - числу опытов N. Это тоже общий результат для этих планов, то есть с помощью планов ПФЭ 2n можно определить все коэффициенты линейного полинома со всеми возможными сочетаниями факторов, включая коэффициенты b12…n, отражающие максимальное взаимодействие факторов вида х1х2…хn. 3. В плане ПФЭ 22 сумма квадратов элементов любого столбца
Поэтому для планов ПФЭ 2n
Таким образом, с помощью планов ПФЭ 2n можно определить свободный член уравнения b0,
План ПФЭ 2n может являться насыщенным, при выборе числа членов уравнения m + 1 = N, ненасыщенным, при выборе числа членов уравнения и соответственно числа столбцов плана m + 1 < N. План ПФЭ 2n является также рототабельным, так как все точки плана лежат на окружности (сфере, гиперсфере) с радиусом Поскольку фиктивная переменная во всех опытах имеет максимальное значение, то для вычисления свободного члена формула имеет вид: b0 = Σ Yj / N. Все коэффициенты регрессии определяются независимо друг от друга. Это свойство приводит к тому, исключение из плана эксперимента тех или иных факторов не потребует проведения все расчетной работы заново. Для плана ПФЭ 23 число факторов n = 3. Выполняется N = 23 = 8 опытов. Уравнение может содержать до восьми членов
Таким образом, формируется план из восьми строк и восемь столбцов. В четвертом столбце (i =3) записываются единицы с чередующимися знаками через четыре элемента. План составляется аналогичным образом плану ПФЭ 22.
Геометрическое отображение плана ПФЭ 23 с указанием номеров точек плана в факторном пространстве представлено на рис. 4.18. Точки плана располагаются в вершинах куба.
Рис. 4.18 Геометрическое отображение плана ПФЭ 23 в факторном пространстве Пример применения плана ПФЭ 22. Пусть в результате проведения экспериментов по плану ПФЭ 22, то есть при изменении двух факторов, мы получили опытные значения Y1, Y2, Y3, Y4. Поверхность, уравнение которой нас интересует, имеет вид рис. 4.19
Рис. 4.19. Поверхность функции отклика
Составляем план ПФЭ 22
Вначале найдем коэффициенты сокращенного линейного полинома вида
и результаты вычислений Рассчитываем коэффициенты полинома.
Полином имеет вид
Результаты расчета по нему приведены в соответствующем столбце плана. Наблюдаются расхождения между Y и
При этом ранее определенные коэффициенты остаются без изменений. Определим коэффициент при дополнительном члене полинома
Полином имеет вид
По нему рассчитываем предсказанные значения отклика в точках плана (столбец
ВОПРОСЫ ДЛЯ САМОПРОВЕРКИ: 1. Что называется активным экспериментом? 2. В чем заключается операция кодирование факторов? 3. В каком случае возможно разложение в степенной ряд функции отклика? 4. Как определяются коэффициенты линейного полинома? Исчисление предикатов Для примера рассмотрим логические модели процессов проектирования технологии механической обработки деталей резанием. Для построения логической модели процесса проектирования технологии механической обработке рассмотрим два основных множества этого процесса: множество С средств обработки и множество А поверхностей детали. Параметрическое описание объектов ai
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 1602; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.12.71.237 (0.144 с.) |
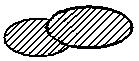

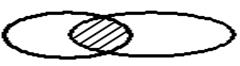
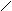
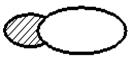
 А Δ В
А Δ В

 Ребро может соединять некоторую вершину саму с собой, такое ребро называют петлей.
Ребро может соединять некоторую вершину саму с собой, такое ребро называют петлей.
 до вершины
до вершины  в графе называется такая последовательность ребер, ведущих от
в графе называется такая последовательность ребер, ведущих от 

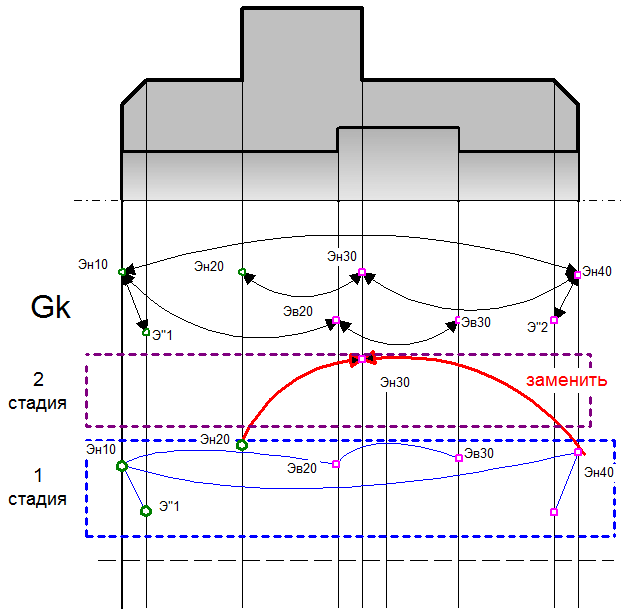
 – начало работы,
– начало работы,  означает, что работа А i+1 не может начаться раньше, чем кончится работа А i. (Нельзя начать монтаж стен, не закончив строить фундамент, чтобы приступить к отделке, нужно иметь на этажах воду, для сварочных работ при монтаже нужно иметь подвод электричества и т.д.)
означает, что работа А i+1 не может начаться раньше, чем кончится работа А i. (Нельзя начать монтаж стен, не закончив строить фундамент, чтобы приступить к отделке, нужно иметь на этажах воду, для сварочных работ при монтаже нужно иметь подвод электричества и т.д.)
 , у которого сумма чисел около вершин наибольшая (это критический путь). В нашем случае получаем путь
, у которого сумма чисел около вершин наибольшая (это критический путь). В нашем случае получаем путь  . Тогда наименьшая возможная продолжительность строительства – 170 дней.
. Тогда наименьшая возможная продолжительность строительства – 170 дней.
 .
. ,
,


 ,
, .
. коэффициентов bi,
коэффициентов bi, 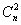 коэффициентов при различных взаимодействиях двух факторов bij,
коэффициентов при различных взаимодействиях двух факторов bij,  коэффициентов тройных взаимодействий факторов bijk, …..,
коэффициентов тройных взаимодействий факторов bijk, …..,  коэффициент b12…n. максимального взаимодействия факторов. Общее число определяемых коэффициентов
коэффициент b12…n. максимального взаимодействия факторов. Общее число определяемых коэффициентов .
. относительно центра плана. В первом столбце матрицы фигурирует фиктивная переменная Х0, необходимая для вычисления свободного члена уравнения регрессии b0. Большее значение переменной согласно принятой программе эксперимента соответствует верхнему уровню и обозначается (+1), меньшее значение – соответствует нижнему уровню и обозначается (-1).
относительно центра плана. В первом столбце матрицы фигурирует фиктивная переменная Х0, необходимая для вычисления свободного члена уравнения регрессии b0. Большее значение переменной согласно принятой программе эксперимента соответствует верхнему уровню и обозначается (+1), меньшее значение – соответствует нижнему уровню и обозначается (-1). .
.



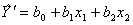
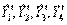 по нему.
по нему. ;
; ;
; .
. .
.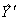 . Если точность сокращенного полинома не удовлетворяет, то по тем же результатам опытов можно сформировать более полный полином вида
. Если точность сокращенного полинома не удовлетворяет, то по тем же результатам опытов можно сформировать более полный полином вида .
.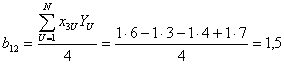 .
. .
. ). Поверхность, построенная по полученному полиному, проходит точно через четыре точки плана (
). Поверхность, построенная по полученному полиному, проходит точно через четыре точки плана ( =0), по которым определены коэффициенты. Однако в других точках области определения функции, например в центре плана (точка 5 в плане, х1 =0, х2 =0), предсказанные и действительные значения, могут не совпадать (
=0), по которым определены коэффициенты. Однако в других точках области определения функции, например в центре плана (точка 5 в плане, х1 =0, х2 =0), предсказанные и действительные значения, могут не совпадать ( =3).
=3). A, ci
A, ci 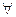 (обобщение операций конъюнкции) и существования – знак
(обобщение операций конъюнкции) и существования – знак  (обобщение операции дизъюнкции).
(обобщение операции дизъюнкции).


