Раздел 3. Графы. Использование графов для моделирования технических систем

Элементы теории графов.

Граф – это некоторая совокупность двух множеств V (точек) и E (линий), между элементами которых определено отношение инцидентности, причем каждый элемент е Î Е инцидентен ровно двум элементам v1,v2 Î V. Элементы множества V называются вершинами графа G, элементы множества Е – его ребрами. Графы удобно изображать в виде рисунков, состоящих из точек и линий, соединяющих некоторые из этих точек. Две вершины соединяются непрерывной линией тогда и только тогда, когда в графе G есть ребро с этими вершинами.

В некоторых случаях инцидентные ребру вершины неравноправны, т.е. они рассматриваются в определенном порядке. Тогда каждому ребру можно приписать направление от первой из инцидентных вершин ко второй. Направленные ребра называют дугами, а граф в этом случае – ориентированным. Первая по порядку вершина, инцидентная ребру ориентированного графа, называется его началом, а вторая – концом. Ребро ориентированного графа выходит из начала и входит в конец. Вершины, соединенные ребром или дугой, называются смежными. Ребра, имеющие общую вершину, также называются смежными. Граф называется полным, если любые две его различные вершины соединены одним и только одним ребром.

Различные ребра могут быть инцидентны одной и той же паре вершин, в этом случае ребра называются кратными, а сам граф часто называют мультиграфом.

 

Ребро может соединять некоторую вершину саму с собой, такое ребро называют петлей.

 

 

При изображении ориентированного графа направления ребер отмечаются стрелками, примыкающими к их концам. Ориентированный граф тоже может иметь кратные ребра и петли, а также соединяющие одни и те же вершины ребра, идущие в противоположных направлениях.

 

 

Матрица инцидентности и список ребер

Задать граф – значит описать множества его вершин и ребер, а также отношение инцидентности. Для описания вершин и ребер графа их надо пронумеровать.

Отношение инцидентности можно определить матрицей ½e_ij½, имеющей m строк и n столбцов. Столбцы соответствуют вершинам графа, строки – ребрам. Если ребро е _i инцидентно вершине v _j, то e_ij = 1, в противном случае e_ij = 0. Матрица инцидентности неориентированного графа является одним из способов его определения (матрица представлена в табл. 8).

Таблица 3.1

Вершины Ребра
	-1
	-1
		-1
			-1

 

В матрице инцидентности ориентированного графа, если вершина v_j – начало ребра, то e_ij = -1; если v_j - конец, то e_ij = 1; если ребро в виде петли, а v_j - инцидентная ей вершина, то e_ij = к, где к – любое число.

В каждой строке матрицы инцидентности для ориентированного или неориентированного графа только два элемента отличны от 0. Поэтому такой способ задания графа оказывается недостаточно экономичным. Отношение инцидентности можно еще задать списком ребер графа. Каждая строка этого списка соответствует ребру, в ней записаны номера вершин, инцидентных ему. Для неориентированного графа порядок этих вершин в строке произволен, для ориентированного первым стоит номер начала ребра, а вторым – его конец.

 

РЕБРА	ВЕРШИНЫ
	1,2
	1,3
	2,4
	3,5

 

По списку ребер графа легко построить его матрицу инцидентности.

Матрица смежности графа

Матрица смежности – это квадратная матрица ½d_ij½, столбцам и строкам которой соответствуют вершины графа. Для неориентированного графа d_ij равно количеству ребер, инцидентных i-й и j- й вершинам, для ориентированного графа этот элемент матрицы смежности равен количеству ребер с началом в i-й вершине и концом в j- й. Таким образом, матрица смежности неориентированного графа симметрична (d_ij = d_ji), а ориентированного не обязательно. Матрица смежности рассмотренных выше графов приведена в табл.3.2, 3.3.

Таблица 3.2 Таблица 3.3

Степени вершин графа

Локальной степенью (или просто степенью) вершин графа называется количество ребер, инцидентных вершине.

Если задана матрица инцидентности, то для каждой j -й вершины r(v_j) = S e_ij, а для матрицы смежности r(v_j) = S d_ij.

Для вершин ориентированного графа определяются две локальные степени: r1(v) - число ребер с началом в вершине v, или, иначе, количество выходящих ребер, и r2(v) - количество входящих в v ребер.

Так как каждое ребро ориентированного графа имеет одно начало и один конец, суммы r1(v) и r2(v) равны количеству ребер графа и равны между собой.

Маршрутом в графе называется такая конечная последовательность ребер (е₀,е₁,…,е_к), что каждые два соседние ребра имеют общую инцидентную вершину, Одно и то же ребро может встречаться в маршруте несколько раз. Если начало и конец маршрута совпадают, то он называется циклическим.

Циклом называется путь, в котором совпадают его начальная и конечная вершины. Простым циклом в графе называется цикл, не проходящий ни через одну из вершин графа более одного раза. Длиной цикла называется число ребер в этом цикле.

Путем от вершины до вершины в графе называется такая последовательность ребер, ведущих от к , в которой любых два соседних ребра имеют общую вершину, но никакое ребро не встречается более одного раза. Вершина называется началом пути, - концом пути. Вершина графа называется начальной, если в нее не входит ни одно ребро, и конечной – если из нее не выходит ни одно ребро. Во всяком графе без циклов есть хотя бы одна начальная и хотя бы одна конечная вершина. Длиной пути называется число ребер этого пути.

Неориентированный граф без циклов (т.е. без петель и кратных ребер) называется лесом. Любая часть леса является деревом. Любую вершину дерева можно отметить и назвать корнем.

Если все ребра дерева ориентировать из корня, то получится ориентированный граф-дерево. В каждую вершину ориентированного граф-дерева входит только одно ребро (а выходить может несколько).

Число вершин граф-дерева на единицу больше числа ребер (рис.2.1).

Рис. 3.1. Ориентированный граф-дерево

3.2.Моделирование технических систем с использованием теории графов.

 

Графы используются при анализе функционирования сложных систем. С отдельными элементами изучаемой системы удобно связывать вершины графа, а взаимодействие парных элементов изображать ребрами графа. Построенный таким образом граф называют

структурным графом системы.

При решении задач создания структуры размерных связей в заготовке модели в виде графов дают наиболее наглядное представление и возможность автоматизировать этот процесс с помощью ЭВМ. Примеры использования графов при решении задач размерного анализа и синтеза приведены на рис. 3.2, 3.3.

 

 

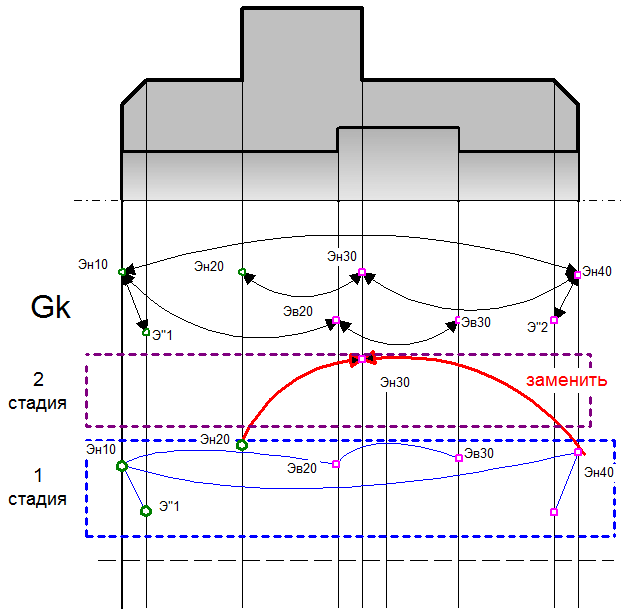
Рис. 3.2 Пример использования графов при решении задачи размерного анализа

 

 

 

Рис. 3.3 Пример использования графов при решении задачи размерного синтеза

 

Граф, изображенный на рис. 3.4 называется сетевым графиком строительства. В данном случае он составлен для строительства жилого дома. Задача: узнать наименьшую возможную продолжительность строительства.

Вершины этого графа обозначают отдельные виды работ на стройке: – начало работы, – прокладка телефонного кабеля; А ₂ – прокладка газовой магистрали; А ₃ – прокладка канализации; А ₄ – прокладка водопровода; А ₅ – прокладка электросети; А ₆ – монтаж стен и перекрытий; А ₇ – отделка; А ₈ – строительство дороги; А ₉ – укладка фундамента; А ₁₀ – строительство котлована; А ₁₁ – благоустройство территории; А ₁₂ – окончание работ.

Ориентация дуги означает, что работа А _i+1 не может начаться раньше, чем кончится работа А _i. (Нельзя начать монтаж стен, не закончив строить фундамент, чтобы приступить к отделке, нужно иметь на этажах воду, для сварочных работ при монтаже нужно иметь подвод электричества и т.д.)

 

 

 

 

Около вершин графа указаны числа – продолжительность в днях соответствующей работы.

Для решения задачи из всех путей ориентированного графа нужно выбрать путь, соединяющий вершины и , у которого сумма чисел около вершин наибольшая (это критический путь). В нашем случае получаем путь . Тогда наименьшая возможная продолжительность строительства – 170 дней.

Замечание. Если сократить, например, время прокладки электросети с 40 до 10 дней, то время строительства не сократится на 30 дней. В этом случае критический путь станет таким: {(А ₀, (А ₀, А ₁₀), А ₁₀, (А ₁₀, А ₉), А ₉, (А ₉, А ₆), А ₆, (А ₆, А ₇), А ₇, (А ₇, А ₁₂), А ₁₂}. Общее время строительства составит 160 дней, т.е. срок сократится только на 10 дней.

ВОПРОСЫ ДЛЯ САМОПРОВЕРКИ:

1. Какой граф называется ориентированным?

2. Что называется маршрутом в графе?

3. Является ли конструкторский граф ориентированным?

4. Что называется локальной степенью вершин графа?