
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Коэффициент ранговой корреляции Кендалла
Для вычисления коэффициента ранговой корреляции Кендалла rk необходимо ранжировать данные по одному из признаков в порядке возрастания и определить соответствующие ранги по второму признаку. Затем для каждого ранга второго признака определяется число последующих рангов, больших по величине, чем взятый ранг, и находится сумма этих чисел. Коэффициент ранговой корреляции Кендалла определяется формулой
где Ri – количество рангов второй переменной, начиная с i +1, величина которых больше чем величина i -ого ранга этой переменной. Существуют таблицы процентных точек распределения коэффициента rk, позволяющие проверить гипотезу о значимости коэффициента корреляции.
распределена приближенно по стандартному нормальному закону.
40. Зависимость между признаками, измеренными в номинальной или порядковой шкалах Часто возникает задача проверки независимости двух признаков, измеренных в номинальной или порядковой шкалах. Пусть у каких-то объектов измеряются два признака X и Y с числом уровней r и s соответственно. Результаты таких наблюдений удобно представлять в виде таблицы, называемой таблицей сопряженности признаков. В таблице ui (i = 1,..., r) и vj (j = 1,..., s) – значения, принимаемые признаками, величина nij – число объектов из общего числа объектов, у которых признак X принял значение ui, а признак Y – значение vj
– количество объектов, у которых встретилось значение ui
– количество объектов, у которых встретилось значение vj
Кроме того, имеют место очевидные равенства
Пусть далее
Дискретные случайные величины X и Y независимы тогда и только тогда, когда
для всех пар i, j
Поэтому гипотезу о независимости дискретных случайных величин X и Y можно записать так:
В качестве альтернативной, как правило, используют гипотезу
Для проверки гипотезы H0 используется статистика
которая при справедливости гипотезы имеет распределение χ 2 с rs − (r + s − 1) степенями свободы. Критерий независимости χ 2 отклоняет гипотезу H0 с уровнем значимости α, если:
41. Регрессионный анализ. Основные понятия регрессионного анализа Для математического описания статистических связей между изучаемыми переменными величинами следует решить следующие задачи: ü подобрать класс функций, в котором целесообразно искать наилучшую (в определенном смысле) аппроксимацию интересующей зависимости; ü найти оценки неизвестных значений параметров, входящих в уравнения искомой зависимости; ü установить адекватность полученного уравнения искомой зависимости; ü выявить наиболее информативные входные переменные. Совокупность перечисленных задач и составляет предмет исследований регрессионного анализа. Функцией регрессии (или регрессией) называется зависимость математического ожидания одной случайной величины от значения, принимаемого другой случайной величиной, образующей с первой двумерную систему случайных величин.
Функции регрессии f (x) и φ (y), не являются взаимно обратимыми, если только зависимость между X и Y не является функциональной. В случае n -мерного вектора с координатами X 1, X 2,…, Xn можно рассматривать условное математическое ожидание для любой компоненты. Например, для X 1
называется регрессией X 1 на X 2,…, Xn.
Для полного определения функции регрессии необходимо знать условное распределение выходной переменной при фиксированных значениях входной переменной. Поскольку в реальной ситуации такой информацией не располагают, то обычно ограничиваются поиском подходящей аппроксимирующей функции fa (x) для f (x), основываясь на статистических данных вида (xi, yi), i = 1,…, n. Эти данные являются результатом n независимых наблюдений y 1,…, yn случайной величины Y при значениях входной переменной x 1,…, xn, при этом в регрессионном анализе предполагается, что значения входной переменной задаются точно.
Проблема выбора наилучшей аппроксимирующей функции fa (x), являясь основной в регрессионном анализе, и не имеет формализованных процедур для своего решения. Иногда выбор определяется на основе анализа экспериментальных данных, чаще из теоретических соображений. Если предполагается, что функция регрессии является достаточно гладкой, то аппроксимирующая ее функция fa (x) может быть представлена в виде линейной комбинации некоторого набора линейно независимых базисных функций ψk (x), k = 0, 1,…, m −1, т. е. в виде
где m – число неизвестных параметров θk (в общем случае величина неизвестная, уточняемая в ходе построения модели). Такая функция является линейной по параметрам, поэтому в рассматриваемом случае говорят о модели функции регрессии, линейной по параметрам. Тогда задача отыскания наилучшей аппроксимации для линии регрессии f (x) сводится к нахождению таких значений параметров, при которых fa (x;θ) наиболее адекватна имеющимся данным. Одним из методов позволяющем решить эту задачу является метод наименьших квадратов.
42. Метод наименьших квадратов Пусть множество точек (xi, yi), i = 1,…, n расположено на плоскости вдоль некоторой прямой
Т. е. в качестве базисных функций здесь выбраны ψ 0(x)≡1 и ψ 1(x)≡ x. Такую регрессию называют простой линейной регрессией. Если множество точек (xi, yi), i = 1,…, n расположено вдоль некоторой кривой, то в качестве fa (x) естественно попробовать выбрать семейство парабол
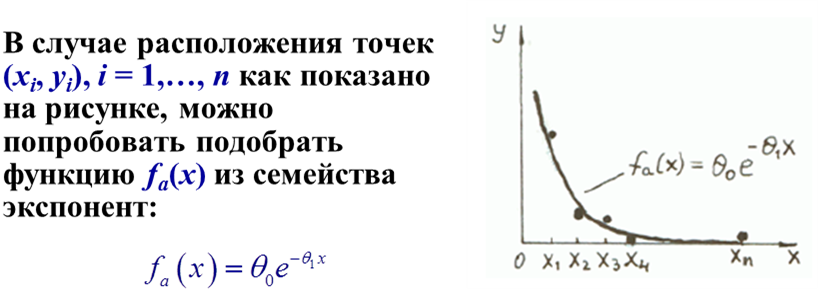
Эта функция является нелинейной по параметрам θ 0 и θ 1, однако путем функционального преобразования (в данном случае логарифмирования) ее можно привести к новой функции f’a (x), линейной по параметрам:
43. Простая линейная регрессия Простейшей моделью регрессии является простая (одномерная, однофакторная, парная) линейная модель, имеющая следующий вид:
где εi – некоррелированные между собой случайные величины (ошибки), имеющие нулевые математические ожидания и одинаковые дисперсии σ 2, a и b – постоянные коэффициенты (параметры), которые необходимо оценить по измеренным значениям отклика yi. Для нахождения оценок параметров a и b линейной регрессии, определяющих наиболее удовлетворяющую экспериментальным данным прямую линию:
применяется метод наименьших квадратов.
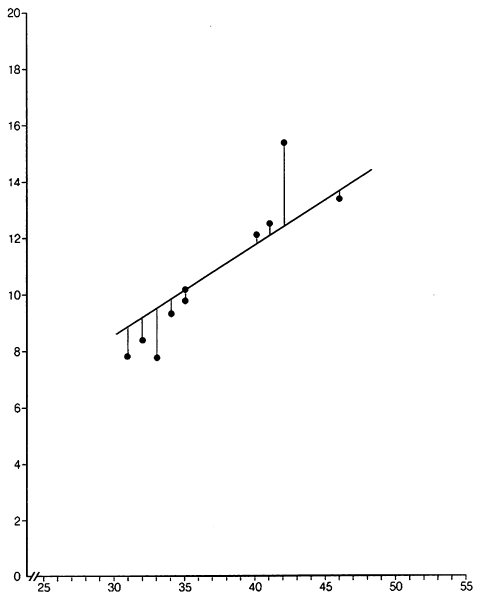
Пусть было произведено десять наблюдений случайной величины Y при фиксированных значениях переменной X
Для минимизации D приравняем к нулю частные производные по a и b:
В результате получим следующую систему уравнений для нахождения оценок a и b:
Решение этих двух уравнений дает:
Выражения для оценок параметров a и b можно представить также в виде:
Тогда эмпирическое уравнение регрессионной прямой Y на X можно записать в виде:
Рассчитаем параметры уравнения регрессии
Таким образом, прямая регрессии имеет вид:
А оценка дисперсии отклонений значений yi oт подобранной прямой линии регрессии
44. Проверка значимости линии регрессии Найденная оценка b ≠ 0 может быть реализацией случайной величины, математическое ожидание которой равно нулю, т. е. может оказаться, что никакой регрессионной зависимости на самом деле нет. Чтобы разобраться с этой ситуацией, следует проверить гипотезу Н0: b = 0 при конкурирующей гипотезе Н1: b ≠ 0. Проверку значимости линии регрессии можно провести с помощью дисперсионного анализа.
Величина yi − ŷi = εi называется остатком и представляет собой разность между двумя величинами: ü отклонением наблюдаемого значения (отклика) от общего среднего откликов; ü отклонением предсказанного значения отклика ŷi от того же среднего
Записанное тождество можно записать в виде
Возведя обе его части в квадрат и просуммировав по i, получим:
полной (общей) суммой квадратов СКп, которая равна сумме квадратов отклонений наблюдений относительно среднего значения наблюдений
сумма квадратов, обусловленной регрессией СКр, которая равна сумме квадратов отклонений значений линии регрессии относительно среднего наблюдений.
Таким образом, разброс Y -ков относительно их среднего значения можно приписать в некоторой степени тому факту, что не все наблюдения лежат на линии регрессии. Если бы это было так, то сумма квадратов относительно регрессии была бы равна нулю. Отсюда следует, что регрессия будет значимой, если сумма квадратов СКр будет больше суммы квадратов СК0. Вычисления по проверки значимости регрессии проводят в следующей таблице дисперсионного анализа
Если ошибки εi распределены по нормальному закону, то при справедливости гипотезы Н0: b = 0 статистика:
распределена по закону Фишера с числом степеней свободы 1 и n −2. Нулевая гипотеза будет отклонена на уровне значимости α, если вычисленное значение статистики F будет больше α-процентной точки f 1; n −2;α распределения Фишера.
45. Проверка адекватности модели регрессии. Метод остатков Под адекватностью построенной регрессионной модели понимается то, что никакая другая модель не дает значимого улучшения в предсказании отклика. Если все значения откликов получены при разных значениях x, т. е. нет нескольких значений отклика, полученных при одинаковых xi, то можно провести лишь ограниченную проверку адекватности линейной модели. Основой для такой проверки являются остатки:
- отклонения от установленной закономерности:
Поскольку X – одномерная переменная, точки (xi, di) можно изобразить на плоскости в виде так называемого графика остатков. Такое представление позволяет иногда обнаружить в поведении остатков какую-то закономерность. Кроме того, анализ остатков позволяет проанализировать предположение относительно закона распределения ошибок.
В случае когда ошибки распределены по нормальному закону и имеется априорная оценка их дисперсии σ 2 (оценка, полученная на основе ранее выполненных измерений), то возможна более точная оценка адекватности модели. С помощью F -критерия Фишера можно проверить, значимо ли остаточная дисперсия s 02 отличается от априорной оценки. Если она значимо больше, то имеет место неадекватность и следует пересмотреть модель. Если априорной оценки σ 2 нет, но измерения отклика Y повторялись два или более раз при одинаковых значениях X, то эти повторные наблюдения можно использовать для получения еще одной оценки σ 2 (первой является остаточная дисперсия). Про такую оценку говорят, что она представляет “чистую” ошибку, поскольку, если сделать x одинаковыми для двух и более наблюдений, то только случайные изменения могут повлиять на результаты и создавать разброс между ними. Получаемая оценка оказывается более надежной оценкой дисперсии, чем оценка, получаемая другими способами. По этой причине при планировании экспериментов имеет смысл ставить опыты с повторениями.
Тогда модель простой линейной регрессии может быть записана в виде:
Эта дисперсия служит оценкой σ 2 безотносительно к тому, корректна ли подобранная модель.
Если возвести обе части этого равенства в квадрат, а затем просуммировать их по j и по i, то получим:
Слева в этом равенстве стоит остаточная сумма квадратов. Первый член в правой части – это сумма квадратов “чистых” ошибок, второй член можно назвать суммой квадратов неадекватности. Последняя сумма имеет m −2 степеней свободы, следовательно, дисперсия неадекватности
При справедливости нулевой гипотезы величина F имеет распределение Фишера со степенями свободы m −2 и n − m. Гипотеза линейности линии регрессии должна быть отвергнута с уровнем значимости α, если полученное значение статистики больше α-процентной точки распределения Фишера с числом степеней свободы m −2 и n − m.
46. Проверка адекватности модели регрессии(см 45). Дисперсионный анализ
47. Проверка адекватности модели регрессии (см 45). Коэффициент детерминации
Чем ближе R 2 к единице, тем лучше регрессия аппроксимирует экспериментальные данные, тем теснее наблюдения примыкают к линии регрессии. Если R 2 = 0, то изменения отклика полностью обусловлены воздействием неучтенных факторов, и линия регрессии параллельна оси x -ов. В случае простой линейной регрессии коэффициент детерминации R 2 равен квадрату коэффициента корреляции r 2 . Максимальное значение R2=1 может быть достигнуто только в случае, когда наблюдения проводились при различных значениях x-ов. Если же в данных имеются повторяющиеся опыты, то величина R2 не может достичь единицы, как бы ни была хороша модель.
48. Доверительные интервалы для параметров простой линейной регрессии Подобно тому как выборочное среднее - это оценка истинного среднего (среднего по совокупности), так и выборочные параметры уравнения регрессии a и b - не более чем оценки истинных коэффициентов регрессии. Разные выборки дают разные оценки среднего — точно так же разные выборки будут давать разные оценки коэффициентов регрессии.
При этом (1 − α) доверительный интервал для оценки дисперсии σ 2 с учетом того, что отношение (n −2) s 02/ σ 2 распределено по закону χ 2 с числом степеней свободы n −2 будет определяться выражением
49. Доверительные интервалы для линии регрессии. Доверительный интервал для значений зависимой переменной Обычно мы не знаем истинных величин коэффициентов регрессии а и b. Нам известны только их оценки. Иначе говоря, истинная прямая регрессии может пройти выше или ниже, быть более крутой или пологой, чем построенная по выборочным данным. Мы вычислили доверительные интервалы для коэффициентов регрессии. Можно вычислить доверительную область и для самой линии регрессии.
Поскольку, то.
Поэтому доверительный интервал для линии регрессии при каждом значении x 0 можно представить в виде
Как видно минимальный доверительный интервал получается при x 0 равному среднему значению и возрастает по мере того, как x 0 “удаляется” от среднего в любом направлении.
|
|||||||||
|
Последнее изменение этой страницы: 2016-07-14; просмотров: 704; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.219.14.63 (0.13 с.) |

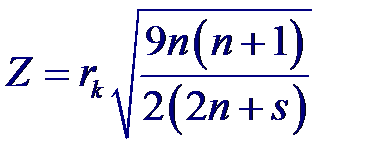 При больших объемах выборки критические значения rk не табулируются, и их приходится вычислять по приближенным формулам, которые основаны на том, что при нулевой гипотезе H0: rk =0 и больших n случайная величина
При больших объемах выборки критические значения rk не табулируются, и их приходится вычислять по приближенным формулам, которые основаны на том, что при нулевой гипотезе H0: rk =0 и больших n случайная величина
 Введем следующие случайные величины:
Введем следующие случайные величины:







 Судить о справедливости гипотезы H0 следует на основании выборочных частот nij таблицы сопряженности. В соответствии с законом больших чисел при n →∞ относительные частоты близки к соответствующим вероятностям:
Судить о справедливости гипотезы H0 следует на основании выборочных частот nij таблицы сопряженности. В соответствии с законом больших чисел при n →∞ относительные частоты близки к соответствующим вероятностям:



 Пусть имеется система случайных величин (X, Y), то функция регрессии Y на X
Пусть имеется система случайных величин (X, Y), то функция регрессии Y на X а функция регрессии X на Y
а функция регрессии X на Y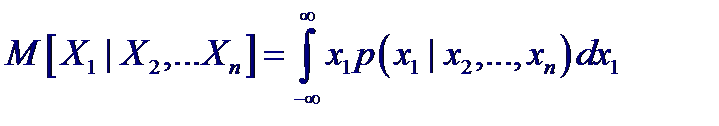
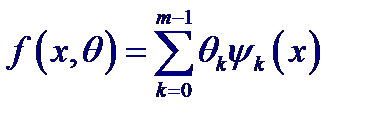
 Тогда в качестве функции fa (x), аппроксимирующей функцию регрессии f (x) = M [ Y | x ] естественно взять линейную функцию аргумента x:
Тогда в качестве функции fa (x), аппроксимирующей функцию регрессии f (x) = M [ Y | x ] естественно взять линейную функцию аргумента x: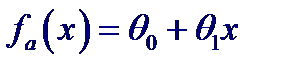
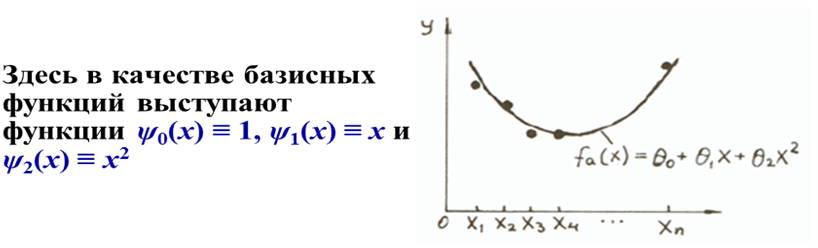




 Согласно методу наименьших квадратов оценки параметров a и b находят из условия минимизации суммы квадратов отклонений значений yi по вертикали от “истинной” линии регрессии:
Согласно методу наименьших квадратов оценки параметров a и b находят из условия минимизации суммы квадратов отклонений значений yi по вертикали от “истинной” линии регрессии:

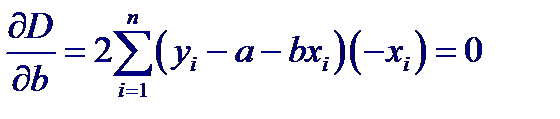


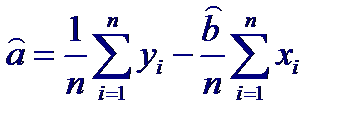



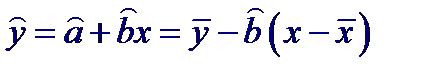
 Несмещенная оценка дисперсии σ 2 отклонений значений yi oт подобранной прямой линии регрессии дается выражением
Несмещенная оценка дисперсии σ 2 отклонений значений yi oт подобранной прямой линии регрессии дается выражением


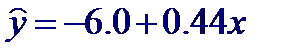

 Рассмотрим следующее тождество:
Рассмотрим следующее тождество:


 Где величины получили название:
Где величины получили название:
 остаточная сумма квадратов СК0. которая равна сумме квадратов отклонений наблюдений относительно значений линии регрессии
остаточная сумма квадратов СК0. которая равна сумме квадратов отклонений наблюдений относительно значений линии регрессии
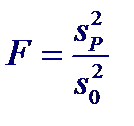




 Предположим, что имеется m различных значений X: x 1, x 2,..., xm. Пусть для каждого из этих значений xi имеется ni наблюдений отклика Y. Всего наблюдений получается:
Предположим, что имеется m различных значений X: x 1, x 2,..., xm. Пусть для каждого из этих значений xi имеется ni наблюдений отклика Y. Всего наблюдений получается:


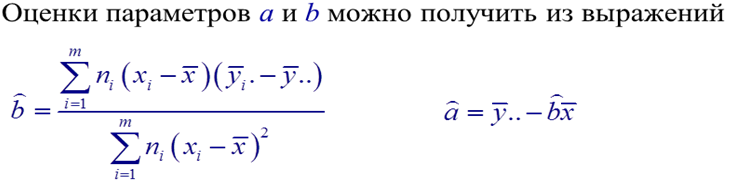

 Найдем дисперсию “чистых” ошибок. Эта дисперсия представляет собой объединенную оценку дисперсии σ 2, если представить значения откликов yij при x = xi как выборки объема ni. В результате дисперсия “чистых” ошибок равна:
Найдем дисперсию “чистых” ошибок. Эта дисперсия представляет собой объединенную оценку дисперсии σ 2, если представить значения откликов yij при x = xi как выборки объема ni. В результате дисперсия “чистых” ошибок равна: Покажем, что сумма квадратов “чистых ошибок” является частью остаточной суммы квадратов (суммы квадратов, входящей в выражение для остаточной дисперсии). Остаток для j -ого наблюдения при xi можно записать в виде:
Покажем, что сумма квадратов “чистых ошибок” является частью остаточной суммы квадратов (суммы квадратов, входящей в выражение для остаточной дисперсии). Остаток для j -ого наблюдения при xi можно записать в виде:

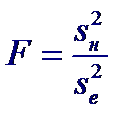 Статистикой критерия для проверки гипотезы H0: простая линейная модель адекватна, против гипотезы H1: простая линейная модель неадекватна, является случайная величина
Статистикой критерия для проверки гипотезы H0: простая линейная модель адекватна, против гипотезы H1: простая линейная модель неадекватна, является случайная величина Иногда для характеристики качества линии регрессии используют выборочный коэффициент детерминации R 2, показывающий, какую часть (долю) сумма квадратов, обусловленная регрессией, СКр составляет в полной сумме квадратов СКп:
Иногда для характеристики качества линии регрессии используют выборочный коэффициент детерминации R 2, показывающий, какую часть (долю) сумма квадратов, обусловленная регрессией, СКр составляет в полной сумме квадратов СКп: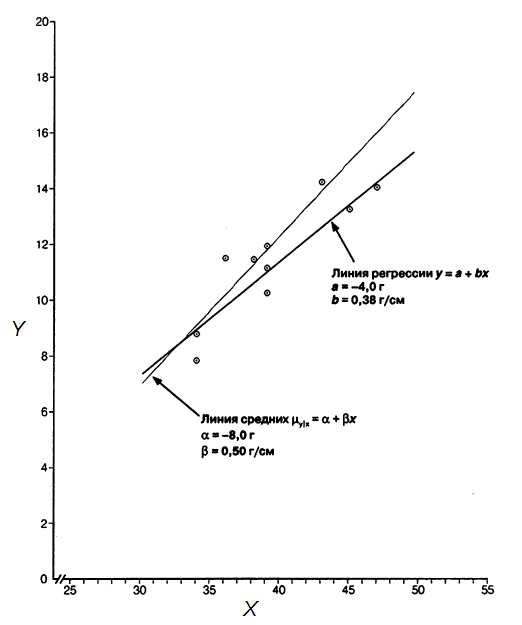
 В предположении, что закон распределения ошибок εi описываются нормальным законом, оценка параметра b будет иметь нормальное распределение с параметрами:
В предположении, что закон распределения ошибок εi описываются нормальным законом, оценка параметра b будет иметь нормальное распределение с параметрами: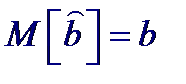
 Поскольку оценка параметра a представляет собой линейную комбинацию независимых нормально распределенных величин, она также будет иметь нормальное распределение с математическим ожиданием и дисперсией:
Поскольку оценка параметра a представляет собой линейную комбинацию независимых нормально распределенных величин, она также будет иметь нормальное распределение с математическим ожиданием и дисперсией:


 Пусть для простой линейной регрессии нужно построить (1− α) доверительный интервал для математического ожидания отклика Y при значении х = х 0. Это математическое ожидание равно a + bх 0, а его оценка
Пусть для простой линейной регрессии нужно построить (1− α) доверительный интервал для математического ожидания отклика Y при значении х = х 0. Это математическое ожидание равно a + bх 0, а его оценка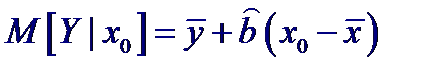

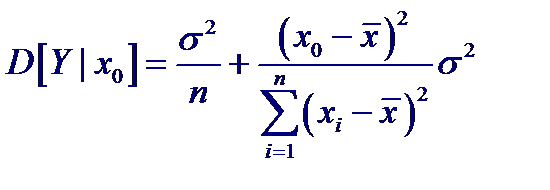 Полученная оценка математического ожидания представляет собой линейную комбинацию некоррелированных нормально распределенных величин и поэтому тоже имеет нормальное распределение с центром в точке истинного значения условного математического ожидания и дисперсией
Полученная оценка математического ожидания представляет собой линейную комбинацию некоррелированных нормально распределенных величин и поэтому тоже имеет нормальное распределение с центром в точке истинного значения условного математического ожидания и дисперсией
 Для получения множества совместных доверительных интервалов, пригодных для всей функции регрессии, на всем ее протяжении, в приведенное выше выражении вместо tn −2, α /2 необходимо подставить
Для получения множества совместных доверительных интервалов, пригодных для всей функции регрессии, на всем ее протяжении, в приведенное выше выражении вместо tn −2, α /2 необходимо подставить



