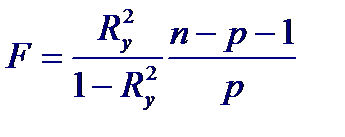Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Вычислительные аспекты обработки данныхСтр 1 из 6Следующая ⇒
Вопросы к экзамену и зачету по курсу “СТАТИСТИЧЕСКИЕ МЕТОДЫ ОБРАБОТКИ ДАННЫХ В ЭКОЛОГИИ”
1. Сущность и цели обработки данных Результатом любого исследования является получение обоснованных выводов об изучаемом объекте или явлении. Эти выводы следует делать на основании соответствующей обработки полученных данных Существующие статистические методы обработки данных являются общепринятыми, а получаемые с их помощью выводы – общепризнанными. Использование этих методов облегчает взаимопонимание между теми, кто выполняет исследования, и теми, для кого оно предназначено, что помогает избегать ошибочных заключений и предотвратить недоразумения. Цель данной дисциплины – изучить современные методы статистической обработки данных, направленные на получение информации об изучаемых объектах Методы статистики позволяют: ü Доказывать правильность и обоснованность используемых методов ü Обосновывать план эксперимента ü Оценить результаты измерения ü Находить зависимости и выявлять наличие различий ü Проверка влияния какого-нибудь фактора на рассматриваемое явление ü Прогнозирование поведения некоторого показателя ü Контроль состояния процесса ü Классификация объектов
2. Основные понятия математической статистики и теории вероятности Математическая статистика – раздел математики, посвященный установлению закономерностей случайных явлений на основании систематизации обработки экспериментальных результатов Теория вероятностей – область математики, занимающаяся изучением закономерностей, порождаемыми случайными событиями Случайное событие – это событие, которое в результате проведенного испытания в зависимости от случайных обстоятельств может либо произойти, либо не произойти Несовместными называются события, если появление одного из них исключает появление других в одном и том же испытании Величина, определяющая, насколько значительны объективные основания рассчитывать на появление события, характеризуется как вероятность события Пусть из всего числа n событий, определенному событию А благоприятствует m событий. Тогда вероятность Р события А равна:
Если события А и B совместны
Событие А называется статистически зависимым от события В, если вероятность события А зависит от того, осуществилось или не осуществилось событие В. Если же вероятность события А не связана с осуществлением события В, то событие А называется статистически независимым от события В Вероятность события А, вычисленная при условии, что произошло событие В, называется условной вероятностью и обозначается через Р (А | В). Если же при вычислении вероятности события А событие В не принимается во внимание, то вероятность Р (А) называется безусловной
Вероятность произведения двух независимых событий равна произведению вероятности одного из них на вероятность другого
Генеральная совокупность – вся совокупность подлежащих изучению объектов или возможных результатов наблюдений над одним объектом Часть элементов отобранных из генеральной совокупности и хорошо представляющих генеральную совокупность, называется выборочной совокупностью или просто выборкой
3. Качество данных. Этапы обработки данных. Вычислительные аспекты обработки данных Первое, с чем сталкивается исследователь при обработке данных, это контроль качества данных, который обычно включает следующие процедуры: ü Проверку данных с целью выявления тех значений, которые логически несовместимы или противоречат предварительным сведениям о границах изменения отдельных переменных ü Выявление резко выделяющихся по своей величине наблюдений ü Восстановление пропущенных наблюдений, включая и наблюдения, которые были исключены по причине их чрезвычайно подозрительного характера ü Проверка однородности нескольких групп исходных данных ü Проверка статистической независимости наблюдений, представляющих исходные данные Этапы обработки данных ü Начальная обработка, т. е. представление исходных данных в подходящей для анализа форме, и проведение проверки качества данных
ü Предварительный анализ данных, направленный на выяснение общей формы данных и предложение путей более обстоятельного анализа ü Итоговый анализ (статистическая обработка), цель которого – дать основу для выводов ü Представление выводов в краткой и ясной форме Оценка эффекта Доверительный интервал для разности средних можно использовать для оценки величины эффекта. Например. Средний диурез при приеме плацебо составил µ1 = 1200 мл, а при приеме препарата - µ2 = 1400 мл. Таким образом, препарат увеличивает суточный диурез на µ1 – µ2 = 1400 – 1200 = 200 мл. Предположим в нашем распоряжении выборки из совокупностей распределенных в соответствии с нормальным законом и необходимо оценить величину эффекта. Для полученных данных значение статистики Стьюдента t = 2,447. Это больше критического значения t для 18 степеней свободы (2,101) и 5% уровня значимости, поэтому можно заключить, что различия статистически значимы, то есть препарат обладает диуретическим действием. В контрольной группе средний диурез составил 1180 мл, а в группе, получавшей диуретик, - 1400 мл. Среднее увеличение диуреза в данном опыте:
Однако как и всякая выборочная оценка, подверженная влиянию случайных факторов, эта величина отличается от истинного увеличения суточного диуреза, равного 200 мл. Поэтому правильнее будет рассчитать доверительный интервал, который покажет диапазон чисел, куда истинное значение величины эффекта попадает с заданной вероятностью.
А стандартная ошибка разности средних
Для определения 95% доверительного интервала (α=100-95) найдем значение t 0,05/2. Объем каждой из выборок n1 = n2 =10. Поэтому число степеней свободы l = 18. Соответствующее значение t 0,05/2 равно 2,101. Отсюда доверительный интервал для среднего изменения диуреза:
26. Доверительный интервал для разности средних. Проверка статистических гипотез с помощью доверительных интервалов
Выражение для статистики Стьюдента можно видоизменить так, чтобы распределение t было всегда симметрично относительно нуля:
Из распределения Стьюдента можно найти такое значение величины t α/2 при котором 100α процентов всех возможных значений t будут расположены левее – t α/2 или правее + t α/2, а остальные 100(1 – α) процентов значений t попадут в интервал от – t α/2 до + t α/2:
преобразуем, полученное неравенство к виду
Таким образом, разность истинных средних отличается от разности выборочных средних менее чем на произведение tα и стандартной ошибки разности выборочных средних. Это неравенство задает доверительный интервал для разности средних µ1 – µ2. Критерий Бартлетта
Бартлетт доказал, что, если справедлива нулевая гипотеза, то статистика
при N → ∞ асимптотически имеет распределение χ2 с k −1 степенями свободы. Однако этот критерий слишком чувствителен к отклонению распределений совокупностей от нормальности, поэтому значимость статистики U2 может указывать не на отсутствие однородности дисперсий, а просто на отклонение от нормальности. Критерий Кочрена основан на статистике:
при этом объемы выборок, по которым рассчитаны sj 2, должны быть одинаковы. Распределение этой статистики известно точно и зависит только от числа степеней свободы n−1 и количества выборок. Нулевая гипотеза H0: все σ j2 равны отвергается с уровнем значимости α, если значение статистики G > Gкр. Критическое значение статистики находят по таблицам процентных точек распределения Кочрена.
31. Непараметрические методы факторного анализа. Ранговый однофакторный анализ. В ряде случаев предположение о нормальности закона распределения остаточных случайных величин в моделях, описанных в дисперсионном анализе, не выполняется. Более того, этот закон оказывается неизвестным. Тогда используют различные непараметрические методы проверки однородности нескольких выборок, из которых наиболее разработаны ранговые методы. Обозначив через rij ранг значения xij, который получит это значение при упорядочении всей совокупности данных в порядке возрастания, придем к следующей таблице данных.
В рамках ранговых критериев нулевая гипотеза формулируется как гипотеза о том, что все k выборок (столбцов таблицы) являются выборками из одного и того же распределения. Строго говоря, если нулевая гипотеза отвергается, то можно только утверждать, что распределения совокупностей различны. Это, однако, не означает, что их средние не равны между собой. Для вывода о том, что выборки производились из совокупностей с различными математическими ожиданиями, необходимо предположить, что эти совокупности одинаковы по всем другим параметрам. Критерий Краскела-Уолллиса.
Если между столбцами нет систематических различий, то средние ранги R.j не должны значительно отличаться от среднего ранга, рассчитанного по всей совокупности рангов. Общее число наблюдений N = n 1 + n 2 + … nk. Для объединенной группы рангами являются числа 1, 2,..., N и общая сумма рангов равна:
Тогда средний ранг для объединенной группы равен: Далее найдем величину, аналогичную межгрупповой сумме квадратов отклонений
Величина СКR зависит от размеров групп. Чтобы получить показатель, отражающий их различия, следует поделить СКR на N (N +1)/12. Полученная величина
является значением критерия Краскела-Уолллиса.
где – сумма рангов j -го столбца.
При больших объемах выборок, которые находятся за пределами таблиц, случайная величина H при справедливости нулевой гипотезы приближенно распределена по закону χ2 с k − 1 степенями свободы. Поэтому в этом приближении нулевая гипотеза отвергается на уровне значимости α, если вычисленное по данным значение статистики H больше χ2k−1;α – α процентной точки распределения χ2 с k−1 степенями свободы.
где g – число групп совпадающих наблюдений; Tj = (tj 3 − tj); tj – число совпадающих наблюдений в группе с номером j.
32. Непараметрические методы факторного анализа. Ранговый двухфакторный анализ без повторений В ряде случаев предположение о нормальности закона распределения остаточных случайных величин в моделях, описанных в дисперсионном анализе, не выполняется. Более того, этот закон оказывается неизвестным. Тогда используют различные непараметрические методы проверки однородности нескольких выборок, из которых наиболее разработаны ранговые методы. Обозначив через rij ранг значения xij, который получит это значение при упорядочении всей совокупности данных в порядке возрастания, придем к следующей таблице данных.
В рамках ранговых критериев нулевая гипотеза формулируется как гипотеза о том, что все k выборок (столбцов таблицы) являются выборками из одного и того же распределения. Строго говоря, если нулевая гипотеза отвергается, то можно только утверждать, что распределения совокупностей различны. Это, однако, не означает, что их средние не равны между собой. Для вывода о том, что выборки производились из совокупностей с различными математическими ожиданиями, необходимо предположить, что эти совокупности одинаковы по всем другим параметрам. Критерий Фридмана Рассмотрим двухфакторный эксперимент, когда на уровнях фактора B проведено по одному наблюдению (неповторяемый эксперимент). Его модель имеет вид
В отличие от дисперсионного анализа нам неизвестно распределение случайных величин εij. Известно только, что оно непрерывно, а сами случайные величины независимы в совокупности и имеют одинаковое распределение. В этом случае для оценки влияния на исследуемый признак факторов A и B используется непараметрический критерий Фридмана, который основан на переходе от значений xij в таблице данных двухфакторного анализа к их рангам.
В отличие от однофакторного анализа ранжирование осуществляется не по всей совокупности величин xij, а по строкам (для проверки однородности данных по столбцам таблицы данных), т. е. ранжируется каждая отдельная строка таблицы данных. Обозначим полученные ранги величин xij через rij. Будем считать, что среди элементов xij, стоящих в одной строке таблицы, нет совпадающих. Определим средние значением рангов по i -му столбцу
При справедливости нулевой гипотезы в силу равновероятности всех перестановок рангов в каждой строке значение Ri. для каждого i не должно сильно отличаться от величины R.. = 0.5(k + 1), представляющей собой общий средний ранг всех элементов таблицы рангов.
При вычислениях удобно использовать другую запись статистики:
Для небольших значений k и n имеются таблицы процентных точек распределения статистики Фридмана, позволяющие при заданном уровне значимости α находить критические значения s (k, n, α). При больших n для определения критических значений пользуются аппроксимацией статистики S. При справедливости нулевой гипотезы статистика в этом случае аппроксимируется распределением χ2 с k −1 степенями свободы. Нулевая гипотеза об однородности данных по столбцам (отсутствие влияния фактора A) принимается с уровнем значимости α, если расчетное значение статистики S меньше критического значения и отвергается, если оно больше критического. Если в строках таблицы данных имеются совпадающие значения, при переходе к таблице рангов используются средние ранги, а вместо статистики S используется ее модификация. Для проверки гипотезы об эффектах фактора B (строк) следует поменять местами строки и столбцы таблицы данных.
33. Корреляционный анализ. Постановка задач статистического исследования зависимостей В математическом анализе зависимость между величинами x и y выражается функцией y = f (x), где каждому значению x соответствует одно и только одно значение y. Такая связь называется функциональной. Для случайных величин X и Y такую зависимость можно установить не всегда. Связь между случайными величинами является не функциональной, а случайной (стохастической), при которой изменение переменной X влияет на значения переменной Y через изменение закона распределения случайной величины Y. Таким образом задача корреляционного анализа исследование наличия взаимосвязей между отдельными группами переменных и установление тесноты (силы) связи между ними. Порядок проведения корреляционного анализа как правило включает: ü выбор показателя статистической связи анализируемых переменных ü оценка значения этого показателя по имеющимся экспериментальным данным, т. е. нахождение его точечной и интервальной оценки ü проверка статистической гипотезы о том, что значение показателя статистической связи значимо отличается от нуля
34. Измерители парной статистической связи. Корреляционное отношение
В процессе наблюдения величины Y = ϕ (X) для каждого фиксированного значения x′ случайной величины X можно иметь разброс значений Y, обусловленный погрешностями прибора или какими-либо неконтролируемыми факторами, и можно вычислить величину дисперсии
Тогда суммарная дисперсия случайной величины Y = ϕ (X) будет состоять из двух слагаемых:
которое показывает долю дисперсии, обусловленную чисто функциональной связью ϕ (X), в полной дисперсии случайной величины Y. Это наиболее общая характеристика степени тесноты связи между случайными величинами Y и X. Очевидно, что 0 ≤ ρ 2 yx ≤ 1. Стремление ρ 2 yx к нулю означает, что доля дисперсии, обусловленная функциональной связью, очень мала. Наоборот, стремление ρ 2 yx к единице показывает, что случайными изменениями Y можно пренебречь и вся дисперсия обусловлена функциональной зависимостью Y = ϕ (X). Аналогично определяется квадрат корреляционного отношения ρ 2 xy переменной X по Y. Однако между ρ 2 yx и ρ 2 xy нет какой-либо простой зависимости. Положительный корень из ρ 2 yx носит название корреляционного отношения, которое является показателем статистической связи между двумя случайными величинами X и Y для самой общей ситуации, когда закон распределения системы (X, Y) является произвольным.
35. Коэффициент корреляции как измеритель степени тесноты связи Рассмотрим двумерную нормальную совокупность, плотность вероятности которой имеет вид
где rxy – коэффициент корреляции между случайными величинами Y и X. Для условной плотности вероятности случайной величины Y (плотности при условии, что случайная величина X приняла определенное значение X = x) получим:
Отсюда видно, что условная плотность вероятности случайной величины Y тоже имеет нормальное распределение с математическим ожиданием
и дисперсией
характеризующей разброс случайной величины Y вокруг математического ожидания. Тогда для квадрата корреляционного отношения получаем
т. е. корреляционное отношение для двумерного нормального распределения совпадает с коэффициентом корреляции. Аналогично можно показать, что ρ 2 xy= r 2 yx, откуда, поскольку r 2 xy= r 2 yx, для нормально распределенных величин ρ 2 xy= ρ 2 yx=r 2.
В общем случае показатели ρ 2 xy и r 2 связаны неравенствами При этом возможны следующие варианты: ü r 2 = ρ 2 yx= 1только тогда, когда имеется строгая линейная функциональная зависимость Y от X ü r 2 < ρ 2 yx= 1только тогда, когда имеется строгая нелинейная функциональная зависимость Y от X ü r 2 = ρ 2 yx< 1 только тогда, когда зависимость Y от X строго линейна, но нет функциональной зависимости ü r 2 < ρ 2 yx< 1 указывает на то, что не существует функциональной зависимости, а некоторая нелинейная кривая “подходит” лучше, чем “наилучшая” прямая линия. Таким образом, в качестве показателя статистической связи между двумя случайными количественными переменными X и Y следует выбрать корреляционное отношение ρyx (или ρxy), если закон распределения системы (X, Y) вызывает сомнение. Если же можно с большой степенью уверенности считать закон распределения системы (X, Y) нормальным, то вместо корреляционного отношения следует использовать коэффициент корреляции r. Анализ частных связей При анализе корреляционных связей могут возникнуть трудности в интерпретации полученных результатов. Полученная сильная корреляционная связь входит в противоречие со здравым смыслом. Подобная ситуация возникает при опосредованном влиянии на оба изучаемых показателя третьего неизвестного фактора и даже целого множества неучтенных факторов. Поэтому необходимо введение таких измерителей статистической связи, которые были бы очищены от влияния других переменных, т. е. давали бы оценку степени тесноты связи при условии, что остальные переменные зафиксированы на некотором постоянном уровне. В этом случае говорят об анализе частных связей и используют частные коэффициенты корреляции.
где rij – коэффициенты корреляции между случайными величинами xi и xj; i, j = 0, 1...., p.
где Aij – алгебраическое дополнение к элементу rij корреляционной матрицы, а J (i, j) = 0, 1...., p за исключением индексов i и j. Например, для трех случайных величин X 0, X 1, X 2 получим корреляционную матрицу вида
Значения точечных оценок частных коэффициентов корреляции получают подстановкой в выражения их выборочных значений. Выборочный частный коэффициент корреляции распределен так же, как и выборочный обычный (парный) коэффициент корреляции, поэтому для проверки гипотез и построения доверительного интервала используются те же самые соотношения, которые были получены ранее с единственной заменой n на n − k, где k – порядок частного коэффициента корреляции (число “ мешающих ” переменных). Анализ множественных связей Оценка степени тесноты связи между входной переменной Y и входными переменными X 1, X 2,..., Xp, осуществляется с помощью множественного коэффициента корреляции Ry. Величина Ry2 показывает, какая доля от полной дисперсии D [ Y ] результирующей переменой Y определяется контролируемым нами изменением функции φ (X 1, X 2,..., Xp):
Для проверки нулевой гипотезы H0: Ry2 = 0 используют статистику:
которая при справедливости гипотезы H0 имеет распределение Фишера с р и n − p −1 степенями свободы. Гипотеза об отсутствии множественной корреляционной связи между Y и X отвергается с уровнем значимости α, если расчетное значение статистики F превышает α-процентную точку распределения Фишера р и n − p −1 степенями свободы.
39. Ранговые коэффициенты корреляции Если необходимо исследовать двумерные данные, закон распределения которых заметно отличается от нормального, то для решения вопроса о некоррелированности или коррелированности этих данных нельзя применять критерии проверки гипотез о значимости коэффициента корреляции, рассмотренные ранее. В этом случае можно воспользоваться методом, основанным на рангах наблюдений каждой переменной и приводящим к коэффициентам ранговой корреляции. Вопросы к экзамену и зачету по курсу “СТАТИСТИЧЕСКИЕ МЕТОДЫ ОБРАБОТКИ ДАННЫХ В ЭКОЛОГИИ”
1. Сущность и цели обработки данных Результатом любого исследования является получение обоснованных выводов об изучаемом объекте или явлении. Эти выводы следует делать на основании соответствующей обработки полученных данных Существующие статистические методы обработки данных являются общепринятыми, а получаемые с их помощью выводы – общепризнанными. Использование этих методов облегчает взаимопонимание между теми, кто выполняет исследования, и теми, для кого оно предназначено, что помогает избегать ошибочных заключений и предотвратить недоразумения. Цель данной дисциплины – изучить современные методы статистической обработки данных, направленные на получение информации об изучаемых объектах Методы статистики позволяют: ü Доказывать правильность и обоснованность используемых методов ü Обосновывать план эксперимента ü Оценить результаты измерения ü Находить зависимости и выявлять наличие различий ü Проверка влияния какого-нибудь фактора на рассматриваемое явление ü Прогнозирование поведения некоторого показателя ü Контроль состояния процесса ü Классификация объектов
2. Основные понятия математической статистики и теории вероятности Математическая статистика – раздел математики, посвященный установлению закономерностей случайных явлений на основании систематизации обработки экспериментальных результатов Теория вероятностей – область математики, занимающаяся изучением закономерностей, порождаемыми случайными событиями Случайное событие – это событие, которое в результате проведенного испытания в зависимости от случайных обстоятельств может либо произойти, либо не произойти Несовместными называются события, если появление одного из них исключает появление других в одном и том же испытании Величина, определяющая, насколько значительны объективные основания рассчитывать на появление события, характеризуется как вероятность события Пусть из всего числа n событий, определенному событию А благоприятствует m событий. Тогда вероятность Р события А равна:
Если события А и B совместны
Событие А называется статистически зависимым от события В, если вероятность события А зависит от того, осуществилось или не осуществилось событие В. Если же вероятность события А не связана с осуществлением события В, то событие А называется статистически независимым от события В Вероятность события А, вычисленная при условии, что произошло событие В, называется условной вероятностью и обозначается через Р (А | В). Если же при вычислении вероятности события А событие В не принимается во внимание, то вероятность Р (А) называется безусловной
Вероятность произведения двух независимых событий равна произведению вероятности одного из них на вероятность другого
Генеральная совокупность – вся совокупность подлежащих изучению объектов или возможных результатов наблюдений над одним объектом Часть элементов отобранных из генеральной совокупности и хорошо представляющих генеральную совокупность, называется выборочной совокупностью или просто выборкой
3. Качество данных. Этапы обработки данных. Вычислительные аспекты обработки данных Первое, с чем сталкивается исследователь при обработке данных, это контроль качества данных, который обычно включает следующие процедуры: ü Проверку данных с целью выявления тех значений, которые логически несовместимы или противоречат предварительным сведениям о границах изменения отдельных переменных ü Выявление резко выделяющихся по своей величине наблюдений ü Восстановление пропущенных наблюдений, включая и наблюдения, которые были исключены по причине их чрезвычайно подозрительного характера ü Проверка однородности нескольких групп исходных данных ü Проверка статистической независимости наблюдений, представляющих исходные данные Этапы обработки данных ü Начальная обработка, т. е. представление исходных данных в подходящей для анализа форме, и проведение проверки качества данных ü Предварительный анализ данных, направленный на выяснение общей формы данных и предложение путей более обстоятельного анализа ü Итоговый анализ (статистическая обработка), цель которого – дать основу для выводов ü Представление выводов в краткой и ясной форме Вычислительные аспекты обработки данных В настоящее время существует большое количество программных средств реализующих различные методы обработки данных: n SPSS, STADIA, STATISTICA, STATGRAPHIKS ЭВРИСТА Тем не менее при использовании пакетов статистических программ принятие решений остается за исследователем. Программа освобождает исследователя только от рутинной вычислительной работы
4. Разновидности исследований. Шкалы измерений Разновидности исследований: ü Эксперимент (активный эксперимент). В этом случае система, над которой осуществляется наблюдение, построена самим исследователем и контролируется им. При этом, как правило, одно из возможных воздействий применяется к каждому объекту наблюдений (экспериментальной единице) и измеряется результат воздействия (отклик) ü Пассивное наблюдение (пассивный эксперимент). В этом случае данные собираются от объектов, входящих в некоторую систему. При этом исследователь не имеет другого контроля над сбором данных, кроме, может быть, некоторого участия в проверке качества данных Шкалы измерений:
|
|||||||||
|
Последнее изменение этой страницы: 2016-07-14; просмотров: 270; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.224.63.87 (0.182 с.) |

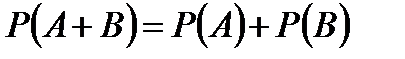 Вероятность суммы двух несовместных событий равна сумме вероятностей этих событий
Вероятность суммы двух несовместных событий равна сумме вероятностей этих событий
 Вероятность произведения двух событий равна произведению вероятности одного из них на условную вероятность другого при условии, что произошло первое:
Вероятность произведения двух событий равна произведению вероятности одного из них на условную вероятность другого при условии, что произошло первое:

 Вычислим стандартную ошибку разности средних. Стандартные отклонения у принимавших диуретик и плацебо составили соответственно 245 и 144 мл. В обеих группах было по 10 человек. Тогда объединенная оценка дисперсии
Вычислим стандартную ошибку разности средних. Стандартные отклонения у принимавших диуретик и плацебо составили соответственно 245 и 144 мл. В обеих группах было по 10 человек. Тогда объединенная оценка дисперсии

 то есть
то есть получаем
получаем
 То есть
То есть
 Пусть из k совокупностей взяты выборки объемами n 1, n 2,... n k и получены оценки дисперсии:
Пусть из k совокупностей взяты выборки объемами n 1, n 2,... n k и получены оценки дисперсии: Тогда для объединенной оценки дисперсии при справедливости нулевой гипотезы H0: σ 12 = σ 22 = … = σk 2 получим:
Тогда для объединенной оценки дисперсии при справедливости нулевой гипотезы H0: σ 12 = σ 22 = … = σk 2 получим: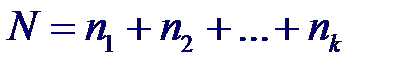

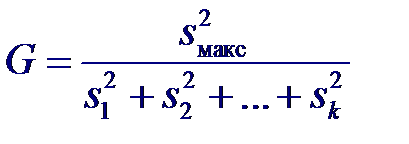

 Вычислим при каждом значении фактора Aj, т. е. для j -го столбца таблицы рангов, значения средних рангов R.j
Вычислим при каждом значении фактора Aj, т. е. для j -го столбца таблицы рангов, значения средних рангов R.j



 Другая форма записи этой статистики, удобная для вычислений, имеет вид
Другая форма записи этой статистики, удобная для вычислений, имеет вид
 Если в таблице данных есть совпадающие значения, необходимо при их ранжировании и переходе к таблице рангов использовать средние ранги. Если совпадений много, то рекомендуется применять модифицированную форму статистики H:
Если в таблице данных есть совпадающие значения, необходимо при их ранжировании и переходе к таблице рангов использовать средние ранги. Если совпадений много, то рекомендуется применять модифицированную форму статистики H:


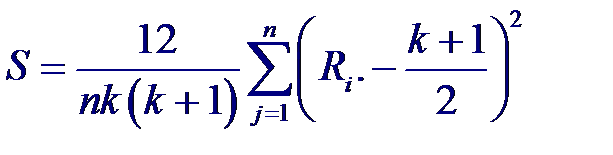 Отсюда статистика Фридмана, используемая для проверки нулевой гипотезы, будет определяться как
Отсюда статистика Фридмана, используемая для проверки нулевой гипотезы, будет определяться как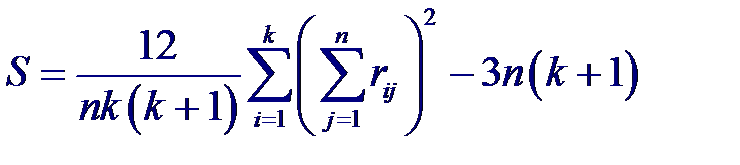
 При функциональных преобразованиях случайных величин вида Y = ϕ (X) для нахождения математического ожидания и дисперсии случайной величины Y достаточно знать закон распределения случайной величины X:
При функциональных преобразованиях случайных величин вида Y = ϕ (X) для нахождения математического ожидания и дисперсии случайной величины Y достаточно знать закон распределения случайной величины X:
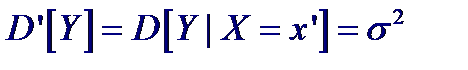

 Первое слагаемое обусловливает вклад в дисперсию от функциональной зависимости Y = ϕ (X), а второе – случайный разброс вокруг математического ожидания M [ ϕ (X)]. Введем понятие квадрата корреляционного отношения
Первое слагаемое обусловливает вклад в дисперсию от функциональной зависимости Y = ϕ (X), а второе – случайный разброс вокруг математического ожидания M [ ϕ (X)]. Введем понятие квадрата корреляционного отношения




 Коэффициент корреляции являются измерителям степени тесноты линейной статистической связи между случайными величинами. Формально его можно вычислить для любой двумерной системы случайных величин, однако только для совместной нормальной совокупности коэффициент корреляции имеет четкий смысл как характеристика тесноты связи.
Коэффициент корреляции являются измерителям степени тесноты линейной статистической связи между случайными величинами. Формально его можно вычислить для любой двумерной системы случайных величин, однако только для совместной нормальной совокупности коэффициент корреляции имеет четкий смысл как характеристика тесноты связи.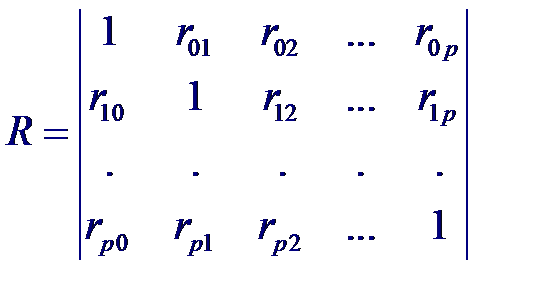 Рассмотрим статистические связи между совокупностью р +1 случайных величин X 0, X 1,..., Xp где переменные X 1,..., Xp являются входными, а переменная X 0 = Y –выходной. Предположим, что случайный вектор (X 0, X 1,..., Xp) имеет нормальный закон распределения. Тогда корреляционная матрица будет иметь вид:
Рассмотрим статистические связи между совокупностью р +1 случайных величин X 0, X 1,..., Xp где переменные X 1,..., Xp являются входными, а переменная X 0 = Y –выходной. Предположим, что случайный вектор (X 0, X 1,..., Xp) имеет нормальный закон распределения. Тогда корреляционная матрица будет иметь вид: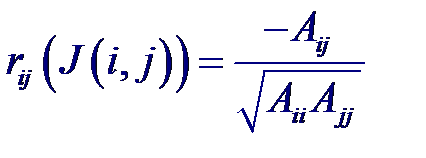 Частный коэффициент корреляции – мера линейной вероятностной зависимости между двумя случайными величинами из некоторой совокупности случайных величин X 0, X 1,..., Xp, когда исключено влияние остальных, т. е. (для пары Xi и Xj)
Частный коэффициент корреляции – мера линейной вероятностной зависимости между двумя случайными величинами из некоторой совокупности случайных величин X 0, X 1,..., Xp, когда исключено влияние остальных, т. е. (для пары Xi и Xj)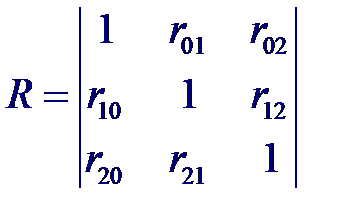
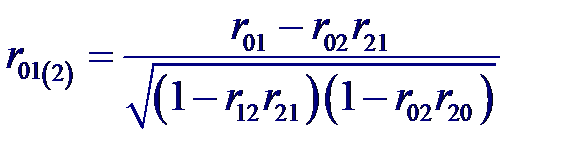 и частный коэффициент корреляции между входной переменной X 0 и выходной X 1 при фиксированном значении переменной X 2
и частный коэффициент корреляции между входной переменной X 0 и выходной X 1 при фиксированном значении переменной X 2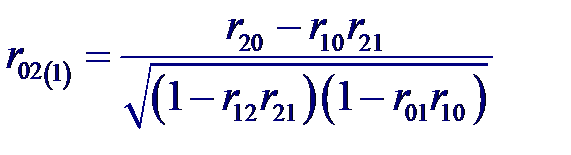 и частный коэффициент корреляции между входной переменной X 0 и выходной X 2 при фиксированном значении переменной X 1
и частный коэффициент корреляции между входной переменной X 0 и выходной X 2 при фиксированном значении переменной X 1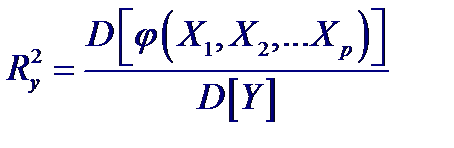
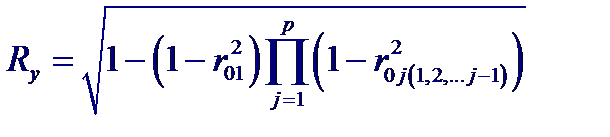 Значение множественного коэффициента корреляции Ry можно вычислить, используя частные коэффициенты корреляции, следующим образом:
Значение множественного коэффициента корреляции Ry можно вычислить, используя частные коэффициенты корреляции, следующим образом: