
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Sслучайные величины, описывающие неопределенные эффекты.
Дисперсионный анализ основан на следующих допущениях относительно случайных величин, описывающих неопределенные (остаточные) эффекты: ü Математическое ожидание каждой остаточной случайной величины равно нулю ü Остаточные случайные величины независимы ü Все остаточные случайные величины имеют одинаковую дисперсию ü Каждая остаточная случайная величина распределена по нормальному закону
23. Однофакторный дисперсионный анализ Рассмотрим простейший случай дисперсионного анализа, когда изучается влияние на исследуемую величину какого-либо одного фактора A. Будем считать, что фактор A изучается на k уровнях A 1, A 2,..., Ak. Пусть для простоты рассмотрения на каждом уровне производится одинаковое число n наблюдений исследуемой величины. Результаты наблюденных значений можно представить в виде таблицы:
Задачей дисперсионного анализа является выяснение вопроса о существенности влияния фактора A на величину X, т. е. вопроса о том, значимо ли отличаются между собой выборочные средние для каждой группы данных. Для этого необходимо проверить нулевую гипотезу H 0: μ1 = μ2 =... = μ k против альтернативной гипотезы H 1: не все μ j равны. Чем больше разброс средних и чем меньше разброс значений внутри групп, тем меньше вероятность того, что наши группы ─ это случайные выборки из одной совокупности. Сформулируем это суждение количественно. Совокупность данных по столбцам таблицы (уровням фактора или группам) при справедливости нулевой гипотезы можно рассматривать как одну выборку объема n х k из генеральной совокупности с математическим ожиданием μ и дисперсией σ2 Оценка генерального среднего:
Кроме того, дисперсию совокупности можно оценить во-первых на основании групповых дисперсий. Такая оценка не будет зависеть от различий групповых средних. Во-вторых, разброс выборочных средних тоже позволяет оценить дисперсию совокупности. Понятно, что такая оценка дисперсии зависит от различий выборочных средних. При справедливости нулевой гипотезы любая из выборочных дисперсий дает одинаково хорошую оценку. Поэтому в качестве оценки дисперсии генеральной совокупности возьмем среднее выборочных дисперсий. Эта оценка называется внутри групповой дисперсией:
Отсюда находим межгрупповую оценку дисперсии:
При справедливости нулевой гипотезы оценки s 2, sA 2, s 02 являются несмещенными оценками генеральной дисперсии σ2. Посмотрим, как ведут себя оценки s 2, sA 2, s 02 при нарушении нулевой гипотезы. Найдем математические ожидания каждой дисперсии для такого случая.
μ – генеральное среднее (математическое ожидание); αj – дифференциальный эффект для уровня j Тогда модель дисперсионного анализа будет иметь вид:
1. для всех i и j 2. 3. для всех i и j
а математическое ожидание внутригрупповой дисперсии s0:
Таким образом, при несправедливости нулевой гипотезы оценка sA 2 является смещенной, при этом смещение определяется суммой квадратов дифференциальных эффектов групп (уровней фактора). Это означает, что при нарушении нулевой гипотезы оценка sA 2 будет иметь тенденцию к возрастанию и тем большую, чем больше отклонение от этой гипотезы.
в случае справедливости нулевой гипотезы подчиняется F -распределению с l 1 = k- 1 и l 2 = k (n- 1) числом степеней свободы. Влияние фактора A на исследуемый признак считается значимым с уровнем значимости α, если
т. е. когда расчетное значение статистики F превышает значение α-процентной точки распределения Фишера. Если это условие не выполняется, то влияние фактора A на исследуемую величину считается незначимым, т.е. математические ожидания μ 1,..., μ k имеют общее генеральное среднее (математическое ожидание) μ,. С другой стороны, если гипотеза H0 отвергается, то делается вывод о том, что некоторые или все μj не совпадают.
Обобщим дисперсионный анализ на случай неравной численности групп. Полная сумма квадратов отклонений значений xij от оценки генерального среднего будет определяться выражением:
Результаты дисперсионного анализа в общем случае обычно представляют в виде следующей таблицы
24. Доверительный интервал для среднего Величина
Математически запись этого выражения имеет вид
Из распределения Стьюдента можно найти такое значение величины t α/2 при котором 100α процентов всех возможных значений t будут расположены левее – t α/2 или правее + t α/2, а остальные 100(1 – α) процентов значений t попадут в интервал от – t α/2 до + t α/2:
преобразуем, полученное неравенство к виду
Таким образом, истинное среднее отличается от выборочного среднего менее чем на произведение t α/2 и стандартной ошибки выборочного среднего s x. Это неравенство задает доверительный интервал для среднего. Приводя k -процентный доверительный интервал среднего, мы утверждаем, что вероятность того, что истинное среднее находится в этом интервале, равна k. Иными словами, если получить все возможные выборки из некоторой совокупности и для каждой рассчитать k -процентный доверительный интервал, то доля интервалов, содержащих среднее по совокупности (истинное среднее), составит k.
25. Доверительный интервал для разности средних. Оценка эффекта Выражение для статистики Стьюдента можно видоизменить так, чтобы распределение t было всегда симметрично относительно нуля:
Из распределения Стьюдента можно найти такое значение величины t α/2 при котором 100α процентов всех возможных значений t будут расположены левее – t α/2 или правее + t α/2, а остальные 100(1 – α) процентов значений t попадут в интервал от – t α/2 до + t α/2:
Таким образом, разность истинных средних отличается от разности выборочных средних менее чем на произведение tα и стандартной ошибки разности выборочных средних. Это неравенство задает доверительный интервал для разности средних µ1 – µ2. Оценка эффекта Доверительный интервал для разности средних можно использовать для оценки величины эффекта. Например. Средний диурез при приеме плацебо составил µ1 = 1200 мл, а при приеме препарата - µ2 = 1400 мл. Таким образом, препарат увеличивает суточный диурез на µ1 – µ2 = 1400 – 1200 = 200 мл. Предположим в нашем распоряжении выборки из совокупностей распределенных в соответствии с нормальным законом и необходимо оценить величину эффекта. Для полученных данных значение статистики Стьюдента t = 2,447. Это больше критического значения t для 18 степеней свободы (2,101) и 5% уровня значимости, поэтому можно заключить, что различия статистически значимы, то есть препарат обладает диуретическим действием.
В контрольной группе средний диурез составил 1180 мл, а в группе, получавшей диуретик, - 1400 мл. Среднее увеличение диуреза в данном опыте:
Однако как и всякая выборочная оценка, подверженная влиянию случайных факторов, эта величина отличается от истинного увеличения суточного диуреза, равного 200 мл. Поэтому правильнее будет рассчитать доверительный интервал, который покажет диапазон чисел, куда истинное значение величины эффекта попадает с заданной вероятностью.
А стандартная ошибка разности средних
Для определения 95% доверительного интервала (α=100-95) найдем значение t 0,05/2. Объем каждой из выборок n1 = n2 =10. Поэтому число степеней свободы l = 18. Соответствующее значение t 0,05/2 равно 2,101. Отсюда доверительный интервал для среднего изменения диуреза:
26. Доверительный интервал для разности средних. Проверка статистических гипотез с помощью доверительных интервалов
Выражение для статистики Стьюдента можно видоизменить так, чтобы распределение t было всегда симметрично относительно нуля:
Из распределения Стьюдента можно найти такое значение величины t α/2 при котором 100α процентов всех возможных значений t будут расположены левее – t α/2 или правее + t α/2, а остальные 100(1 – α) процентов значений t попадут в интервал от – t α/2 до + t α/2:
преобразуем, полученное неравенство к виду
Таким образом, разность истинных средних отличается от разности выборочных средних менее чем на произведение tα и стандартной ошибки разности выборочных средних. Это неравенство задает доверительный интервал для разности средних µ1 – µ2.
|
|||||||
|
Последнее изменение этой страницы: 2016-07-14; просмотров: 297; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.137.162.110 (0.044 с.) |

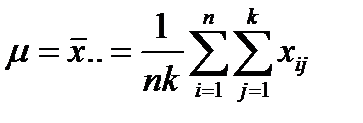
 Несмещенная оценка дисперсии генеральной совокупности:
Несмещенная оценка дисперсии генеральной совокупности:
 Оценим теперь дисперсию совокупности по выборочным средним. Поскольку мы предположили, что все выборки извлечены из одной совокупности, то стандартное отклонение выборочных средних будет служить оценкой ошибки среднего:
Оценим теперь дисперсию совокупности по выборочным средним. Поскольку мы предположили, что все выборки извлечены из одной совокупности, то стандартное отклонение выборочных средних будет служить оценкой ошибки среднего:
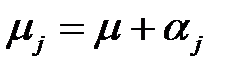 Отклонение от нулевой гипотезы означает, что математическое ожидание в j -й группе может быть представлено в виде:
Отклонение от нулевой гипотезы означает, что математическое ожидание в j -й группе может быть представлено в виде: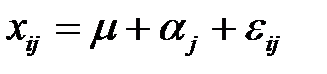
 Отсюда следует, что:
Отсюда следует, что:
 При справедливости допущений:
При справедливости допущений: случайные величины ε ij взаимно независимы
случайные величины ε ij взаимно независимы Математическое ожидание межгрупповой дисперсии sA:
Математическое ожидание межгрупповой дисперсии sA:
 В результате задача проверки гипотезы H0 сводится к проверке гипотезы о равенстве дисперсий sA2 и s02. При справедливости допущения о нормальном распределении случайных величин εij отношение:
В результате задача проверки гипотезы H0 сводится к проверке гипотезы о равенстве дисперсий sA2 и s02. При справедливости допущения о нормальном распределении случайных величин εij отношение: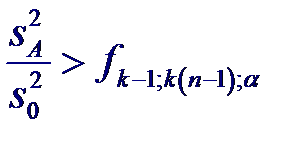


 Поскольку сумма квадратов между группами СК A имеет k − 1 степеней свободы, а сумма квадратов внутри групп СК0 имеет ∑nj − k степеней свободы, то оценки межгрупповой (факториальной) и внутригрупповой (остаточной) дисперсий имеют соответственно вид:
Поскольку сумма квадратов между группами СК A имеет k − 1 степеней свободы, а сумма квадратов внутри групп СК0 имеет ∑nj − k степеней свободы, то оценки межгрупповой (факториальной) и внутригрупповой (остаточной) дисперсий имеют соответственно вид: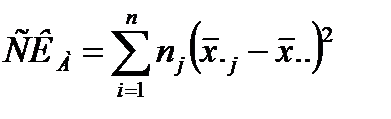

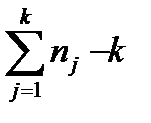

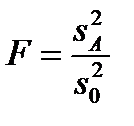






 подчиняется распределению Стьюдента.
подчиняется распределению Стьюдента.


 То есть
То есть
 преобразуем, полученное неравенство к виду
преобразуем, полученное неравенство к виду
 Вычислим стандартную ошибку разности средних. Стандартные отклонения у принимавших диуретик и плацебо составили соответственно 245 и 144 мл. В обеих группах было по 10 человек. Тогда объединенная оценка дисперсии
Вычислим стандартную ошибку разности средних. Стандартные отклонения у принимавших диуретик и плацебо составили соответственно 245 и 144 мл. В обеих группах было по 10 человек. Тогда объединенная оценка дисперсии
 то есть
то есть получаем
получаем


