
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Теорема Гьоделя про неповноту будь-якої формальної аксіоматичної теорії.
Система аксіом евклідової геометрії Д.Гільберта та наслідки з неї. Вперше аксіоматичне обгрунтування геометрії Евкліда було здійснено в 1899 році видатним німецьким математиком Д.Гільбертом (1862-1943). Трохи пізніше з’явились інші аксіоматики — Пеано, Кагана, Шура та ін. Аксіоматика гільберта містить 20 аксіом, які описують три основні поняття (точка, пряма, площина) і п’ять основних відношень: Г 1 (належність точки прямій), Г 2 (належність точки площині), Г 3 ("лежати між" для трьох точок однієї прямої), Г 4 (конгруентність одного відрізка другому), Г 5 (конгруентність кута куту). Система аксіом Гільберта складається з 5 груп, які описують відношення основними об’єктами. Містить п'ять груп аксіом: 1. Аксіоми належності. 2. Аксіоми порядку. 3. Аксіоми конгруентності. 4. Аксіоми неперервності. 5. Аксіома паралельності.
Аксіоми належності 1.1. Для будь-яких двох точок А і В існує пряма а, яка належить кожній з цих двох точок. 1.2. Для двох точок А і В існує не більше однієї прямої, яка належить кожній з точок А, В. 1.3. На прямій існують принаймні дві точки. Існують принаймні три точки, що не лежать на одній прямій. 1.4. Для будь яких-точок А, В, С, що не лежать на одній прямій, існує площина a, що належить кожній з трьох точок А, В, С. Для будь-якої площини завжди існує точка, що належить їй. 1.5. Для будь-яких трьох точок А, В, С, що не лежать на одній і тій же прямій, існує не більше, ніж одна площина, що належить цим точкам. 1.6. Якщо дві точки А і В прямої а лежать в площині a, то кожна точка прямої а лежить в площині a. 1.7. Якщо дві площини a і b мають спільну точку А, то вони мають принаймні ще одну спільну точку В. 1.8. Існують принаймні чотири точки, що не лежать в одній площині. Наслідок 1. Дві прямі мають не більше однією спільної точки. Наслідок 2. Якщо дві площини мають спільну точку, то вони мають спільну пряму, на якій лежать всі спільні точки цих двох площин. Наслідок 3. Через пряму і точку, що не лежить на ній, так само як і через дві прямі, що перетинаються, можна провести площину і тільки одну.
Наслідок 4. На кожній площині існує три точки, що не лежать на одній прямій.
2. Аксіоми порядку 2.1. Якщо точка В лежить між точками А і С, то А, В, С — різні точки і В лежить між С і А. 2.2. Для будь-яких двох точок А і С на прямій АС існує принаймні одна точка В така, що точка С лежить між А і В. 2.3. Серед будь-яких трьох точок прямої існує не більше, ніж одна точка, що лежить між двома іншими. 2.4. Нехай А, В, С — три точки, що не лежать на одній прямій, і а — пряма в площині АВС, що не проходить через жодну з точок А, В, С; якщо при цьому пряма а проходить через одну з точок відрізка АВ, то вона повинна пройти через одну з точок відрізка АС чи через одну з точок відрізка ВС. (Аксіома Паша). Перша та друга групи аксіом дозволяють ввести такі важливі поняття геометрії, як поняття площини, променя і півпростору Наслідок 2.1. Пряма а, що лежить в площині a, розділяє множину точок цієї площини, що не лежать на прямій а, на дві непорожні підмножини так, що якщо точки А і В належать одній підмножині, то відрізок АВ не має спільних точок з прямою а; якщо ж ці точки належать різним підмножинам, то відрізок АВ має спільну точку з прямою а. Наслідок 2.2. Якщо промінь виходить з вершини кута і має хоча б одну внутрішню точку цього кута, то він перетинає будь-який відрізок з кінцями на різних сторонах цього кута. 3. Аксіоми конгруентності 3.1. Якщо А і В є різними точками на прямій а і 3.2. Якщо два відрізки конгруентні третьому, то вони конгруентні між собою. 3.3. Нехай АВ і ВС є відрізками прямої а, що не мають жодної спільної точки, і хай, далі, 3.4. Від даної півпрямої в дану півплощину, що визначається цією півпрямою і її продовженням, можна відкласти, і притому лише один, кут, конгруентний даному куту. 3.5. Якщо у двох трикутників АВС і А 1 В 1 С 1 АВ = А 1 В 1, АС = А 1 С 1 і
Аксіоми неперервності 4.1. (Аксіома Архімеда). Нехай АВ і СD — два будь-яких відрізки; тоді на прямій АВ існує скінченна кількість точок А 1, А 2, А 3,..., Аn таких, що відрізки АА 1, АА 2, АА 3,..., Аn -1 An конгруентні відрізку СD і точка В лежить між А і Аn. 4.2. (Аксіома лінійної повноти). Точки прямої утворюють систему, яка при збереженні лінійного порядку, першої аксіоми про конгруентність і аксіоми Архімеда не допускає ніякого розширення, тобто до цієї системи точок не можна додати ще точки так, щоб в системі, утвореної початковими точками і точками, що додались, виконувались всі вказані аксіоми. 4.3. (Акміома Кантора). Нехай на довільній прямій а задано нескінченну послідовність відрізків Зрозуміло, що точка М єдина. Дійсно, якщо припустити, що точка N, відмінна від точки М, також належить кожному з відрізків даної послідовності, то отримаємо Можна довести, що аксіоми 4.1 і 4.3 еквівалентні наступному твердженню Дедекінда. 4.4. (Аксіома Дедекінда)Нехай дано розбиття точок відрізка 1) 2) довільна точка класу К 1, відмінна від точки А, лежить між точкою А і будь-якою точкою класу К 2. Тоді існує точка М 0 відрізка Розбиття відрізка Аксіома паралельності. Нехай а — довільна пряма, і А — точка, що лежить поза нею; в такому випадку в площині, що визначається прямою а і точкою А, існує не більше ніж одна пряма, що проходить через точку А і не перетинає пряму а.
|
||||||
|
Последнее изменение этой страницы: 2016-07-11; просмотров: 650; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.17.5.68 (0.009 с.) |
 Не існує системи аксіом, з якої були б вивідними всі замкнуті формули
Не існує системи аксіом, з якої були б вивідними всі замкнуті формули


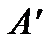 — точка на тій же прямій або на іншій прямій
— точка на тій же прямій або на іншій прямій  , то завжди можна знайти точку
, то завжди можна знайти точку  , що лежить по одну від точки
, що лежить по одну від точки  .
. є відрізками тієї ж прямої чи іншої прямої
є відрізками тієї ж прямої чи іншої прямої  , то й
, то й 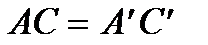 .
. , то в них
, то в них  ,
,  .
. з яких кожний наступний міститься всередині попереднього і, крім того, для довільного відрізка CD існує натуральне число п, таке, що
з яких кожний наступний міститься всередині попереднього і, крім того, для довільного відрізка CD існує натуральне число п, таке, що  . Тоді на прямій а існує точка М, яка належит кожному з відрізків даної послідовності.
. Тоді на прямій а існує точка М, яка належит кожному з відрізків даної послідовності. для будь-якого п, що суперечить аксіомі.
для будь-якого п, що суперечить аксіомі. на два класи К 1 і К 2 (тобто
на два класи К 1 і К 2 (тобто  ), що задовольняє двом умовам:
), що задовольняє двом умовам: і класи К 1 і К 2 містять точки, відмінні від точок А і В;
і класи К 1 і К 2 містять точки, відмінні від точок А і В;


