
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Історичний огляд розвитку основ геометрії. Розвиток евклідової геометрії.Стр 1 из 9Следующая ⇒
Питання до екзамену з основ геометрії 1. Історичний огляд розвитку основ геометрії. Розвиток евклідової геометрії. 2. Аксіоматичний метод побудови наукової теорії. Вимоги до системи аксіом, їх сутність і способи доведення. 3. Змістовні та формальні аксіоматичні теорії. 4. Теорема Гьоделя про неповноту будь-якої формальної аксіоматичної теорії. 5. Істинні, хибні та формально нерозв’язні твердження. 6. Геометрична, арифметична та алгебраїчна моделі системи аксіом. 7. Система аксіом евклідової геометрії Д. Гільберта та наслідки з неї. 8. Система аксіом евклідової геометрії Г. Вейля. 9. Доведення теорем евклідової геометрії в системі аксіом Г. Вейля. 10. Абсолютна геометрія. 11. Аксіоми вимірювання довжин відрізків. 12. Теорема про вимірювання довжин відрізків. Одиниці вимірювання довжин відрізків. 13. Аксіоми вимірювання площ многокутників. Одиниці вимірювання площ многокутників. 14. Теореми: 1) про площу прямокутника; 2) про площу трапеції; 3) про площу трикутника; 4) про незалежність площі трикутника від вибору тієї чи іншої його сторони; 5) про площу паралелограма. 15. Теорема про існування та єдиність площі многокутника. 16. Означення та властивості рівновеликих і рівноскладених многокутників. 17. Теорема про рівноскладеність прямокутника і паралелограма. 18. Теорема про рівноскладені паралелограми. 19. Теорема про рівноскладені трикутники. 20. Теорема про рівноскладеність многокутника і трикутника. 21. Теорема Бойяі-Гервіна про рівноскладені многокутники. 22. Взаємозв’язок відношень рівновеликості та рівноскладеності многокутників. 23. Аксіоми вимірювання об’ємів многогранників. Одиниці вимірювання об’ємів многогранників. 24. Означення і властивості рівновеликих і рівноскладених многогранників. 25. Теорема Дена-Кагана про необхідні і достатні умови рівноскладеності многогранників. 26. Означення кубованого тіла. Теорема про необхідну умову кубованості просторового тіла. 27. Історичний розвиток неевклідової геометрії М.І. Лобачевського. 28. Система аксіом площини Лобачевського. 29. Аксіома паралельності Лобачевського та наслідки з неї. 30. Теорема про суму внутрішніх кутів трикутника на площині Лобачевського. 31. Теорема про існування безлічі прямих, які проходять через задану точку, яка не належить даній прямій, і даної прямої не перетинають.
32. Означення паралельних прямих на площині Лобачевського. 33. Кут паралельності, стрілка кута паралельності та їх властивості. 34. Теорема про те, що будь-який гострий кут на площині Лобачевського може бути кутом паралельності. 35. Функція Лобачевського та її властивості. 36. Означення та ознака розбіжних прямих. 37. Теореми про властивості розбіжних прямих. 38. Теорема про існування та єдиність спільного перпендикуляра до двох розбіжних прямих. 39. Теорема про відстань між розбіжними прямими на площині Лобачевського. 40. Теореми про властивості паралельних прямих на гіперболічній площині. 41. Теорема про відстань між паралельними прямими на площині Лобачевського. 42. Ознаки рівності трикутників на площині Лобачевського. Четверта ознака рівності трикутників на площині Лобачевського та наслідки з неї. 43. Теорема про медіатриси трикутника. Види трикутників на гіперболічній площині. 44. Осі симетрії сукупності двох прямих. 45. Означення і властивості кривих на гіперболічній площині. 46. Властивості дотичних до кривих на площині Лобачевського. 47. Криві сталої кривини
Історичний огляд розвитку основ геометрії. Розвиток евклідової геометрії. І. Витоки геометрії відносяться до глибокої давнини, коли вона зародилася у зв’язку з практичними потребами у вимірюванні площі ділянок землі та об’ємів тіл. Геометрія тоді являла собою механічну суміш не пов’язаних між собою геометричних фактів. Це була епоха попереднього накопичення геометричних відомостей. Найбільшого розвитку геометричних знань досягли древньосхідні цивілізації: Єгипет, Вавилон, Індія, Китай. ІІ. Основні періоди розвитку грецької математики до Евкліда. В 7 ст. до н. е. геометричні знання попадають з Єгипту в Грецію. Тут у зв'язку з загальним розвитком економіки, науки, геометрія отримала широкий розвиток і корінні зміни. Греки звільнили геометрію від вузько прикладного характеру і перетворили в строго теоретичну науку. Розвиток грецької геометрії можна поділити на три періоди:
1. 7-6 ст. до н. є - індійський, Мала Азія. Засновник - Фалес Мілецький. 2. 6-5 ст. до н.е. Батьківщина - Південна Італія. Засновники – Піфагор і школа. 3. 4 ст. до н.е. Батьківщина - Афіни. Школа Платона і Аристотеля. Евдокс Кнідський і Менехм. ІІІ. Пов’язаний з виданням “Початків Евкліда”, 3 ст. до н.е. IV. 19 ст. - виникнення неевклідової геометрії Лобачевського, неевклідової геометрії Рімана. Основи геометрії – це розділ геометрії, в якому досліджуються основні поняття геометрії, співвідношення між ними і пов’язані з ними відношення. Основні задачі вивчення курсу основ геометрії: 1. Ознайомити з еволюцією основних геометричних ідей. 2. Осмислити елементи геометрії в її сучасному розумінні, вивчити логічну базу та її логічну структуру. 3.Вивчити елементи неевклідової геометрії. Проблема повної аксіоматизації елементарної геометрії — одна з проблем геометрії, що виникла у Стародавній Греції у зв'язку з критикою цієї першої спроби побудувати повну систему аксіом так, щоб всі твердження евклідової геометрії з цих аксіом були чисто логічним висновком без унаочнювальних креслень. У «Началах» Евкліда, була дана наступна аксіоматика: 1.Від усякої точки до всякої точки можна провести пряму лінію. 2.Обмежену лінію можна безперервно продовжувати до прямої. 3.З усякого центра довільним розхилом циркуля може бути описане коло. 4.Усі прямі кути рівні між собою. 5.Якщо пряма, що перетинає дві прямі, утворює внутрішні односторонні кути, які менші ніж два прямі кути, то ці дві прямі, продовжені необмежено, зустрінуться з тієї сторони, де кути менші за два прямі. Аксіома паралельності Евкліда Дослідження системи аксіом Евкліда в другій половині XIX століття показало її неповноту. У 1899 році Давид Гільберт запропонував першу достатньо строгу аксіоматику евклідової геометрії. Спроби поліпшення евклідової аксіоматики робилися і до Гільберта, проте підхід Гільберта, при всій його консервативності у виборі понять, виявився найуспішнішим. «Начала» Евкліда. Ця праця і понині залишається зразковим викладенням у дусі аксіоматичного методу: всі положення виводяться логічним шляхом з невеликого числа явно зазначених і не доводимих припущень — аксіом. Геометрія греків, звана сьогодні евклідовою, або елементарною, займалася вивченням простих форм: прямих, площин, відрізків, правильних багатокутників і багатогранників, конічних перерізів, а також куль, циліндрів, призм, пірамід і конусів. Обчислюються їхні площі і об'єми. Перетворення в основному обмежувалися геометричною подібністю.
Теорема Гьоделя про неповноту будь-якої формальної аксіоматичної теорії. Система аксіом евклідової геометрії Д.Гільберта та наслідки з неї. Вперше аксіоматичне обгрунтування геометрії Евкліда було здійснено в 1899 році видатним німецьким математиком Д.Гільбертом (1862-1943). Трохи пізніше з’явились інші аксіоматики — Пеано, Кагана, Шура та ін. Аксіоматика гільберта містить 20 аксіом, які описують три основні поняття (точка, пряма, площина) і п’ять основних відношень: Г 1 (належність точки прямій), Г 2 (належність точки площині), Г 3 ("лежати між" для трьох точок однієї прямої), Г 4 (конгруентність одного відрізка другому), Г 5 (конгруентність кута куту).
Система аксіом Гільберта складається з 5 груп, які описують відношення основними об’єктами. Містить п'ять груп аксіом: 1. Аксіоми належності. 2. Аксіоми порядку. 3. Аксіоми конгруентності. 4. Аксіоми неперервності. 5. Аксіома паралельності.
Аксіоми належності 1.1. Для будь-яких двох точок А і В існує пряма а, яка належить кожній з цих двох точок. 1.2. Для двох точок А і В існує не більше однієї прямої, яка належить кожній з точок А, В. 1.3. На прямій існують принаймні дві точки. Існують принаймні три точки, що не лежать на одній прямій. 1.4. Для будь яких-точок А, В, С, що не лежать на одній прямій, існує площина a, що належить кожній з трьох точок А, В, С. Для будь-якої площини завжди існує точка, що належить їй. 1.5. Для будь-яких трьох точок А, В, С, що не лежать на одній і тій же прямій, існує не більше, ніж одна площина, що належить цим точкам. 1.6. Якщо дві точки А і В прямої а лежать в площині a, то кожна точка прямої а лежить в площині a. 1.7. Якщо дві площини a і b мають спільну точку А, то вони мають принаймні ще одну спільну точку В. 1.8. Існують принаймні чотири точки, що не лежать в одній площині. Наслідок 1. Дві прямі мають не більше однією спільної точки. Наслідок 2. Якщо дві площини мають спільну точку, то вони мають спільну пряму, на якій лежать всі спільні точки цих двох площин. Наслідок 3. Через пряму і точку, що не лежить на ній, так само як і через дві прямі, що перетинаються, можна провести площину і тільки одну. Наслідок 4. На кожній площині існує три точки, що не лежать на одній прямій.
2. Аксіоми порядку 2.1. Якщо точка В лежить між точками А і С, то А, В, С — різні точки і В лежить між С і А. 2.2. Для будь-яких двох точок А і С на прямій АС існує принаймні одна точка В така, що точка С лежить між А і В. 2.3. Серед будь-яких трьох точок прямої існує не більше, ніж одна точка, що лежить між двома іншими. 2.4. Нехай А, В, С — три точки, що не лежать на одній прямій, і а — пряма в площині АВС, що не проходить через жодну з точок А, В, С; якщо при цьому пряма а проходить через одну з точок відрізка АВ, то вона повинна пройти через одну з точок відрізка АС чи через одну з точок відрізка ВС. (Аксіома Паша). Перша та друга групи аксіом дозволяють ввести такі важливі поняття геометрії, як поняття площини, променя і півпростору
Наслідок 2.1. Пряма а, що лежить в площині a, розділяє множину точок цієї площини, що не лежать на прямій а, на дві непорожні підмножини так, що якщо точки А і В належать одній підмножині, то відрізок АВ не має спільних точок з прямою а; якщо ж ці точки належать різним підмножинам, то відрізок АВ має спільну точку з прямою а. Наслідок 2.2. Якщо промінь виходить з вершини кута і має хоча б одну внутрішню точку цього кута, то він перетинає будь-який відрізок з кінцями на різних сторонах цього кута. 3. Аксіоми конгруентності 3.1. Якщо А і В є різними точками на прямій а і 3.2. Якщо два відрізки конгруентні третьому, то вони конгруентні між собою. 3.3. Нехай АВ і ВС є відрізками прямої а, що не мають жодної спільної точки, і хай, далі, 3.4. Від даної півпрямої в дану півплощину, що визначається цією півпрямою і її продовженням, можна відкласти, і притому лише один, кут, конгруентний даному куту. 3.5. Якщо у двох трикутників АВС і А 1 В 1 С 1 АВ = А 1 В 1, АС = А 1 С 1 і Аксіоми неперервності 4.1. (Аксіома Архімеда). Нехай АВ і СD — два будь-яких відрізки; тоді на прямій АВ існує скінченна кількість точок А 1, А 2, А 3,..., Аn таких, що відрізки АА 1, АА 2, АА 3,..., Аn -1 An конгруентні відрізку СD і точка В лежить між А і Аn. 4.2. (Аксіома лінійної повноти). Точки прямої утворюють систему, яка при збереженні лінійного порядку, першої аксіоми про конгруентність і аксіоми Архімеда не допускає ніякого розширення, тобто до цієї системи точок не можна додати ще точки так, щоб в системі, утвореної початковими точками і точками, що додались, виконувались всі вказані аксіоми. 4.3. (Акміома Кантора). Нехай на довільній прямій а задано нескінченну послідовність відрізків Зрозуміло, що точка М єдина. Дійсно, якщо припустити, що точка N, відмінна від точки М, також належить кожному з відрізків даної послідовності, то отримаємо Можна довести, що аксіоми 4.1 і 4.3 еквівалентні наступному твердженню Дедекінда. 4.4. (Аксіома Дедекінда)Нехай дано розбиття точок відрізка 1) 2) довільна точка класу К 1, відмінна від точки А, лежить між точкою А і будь-якою точкою класу К 2. Тоді існує точка М 0 відрізка Розбиття відрізка
Аксіома паралельності. Нехай а — довільна пряма, і А — точка, що лежить поза нею; в такому випадку в площині, що визначається прямою а і точкою А, існує не більше ніж одна пряма, що проходить через точку А і не перетинає пряму а. АКСІОМИ ДОДАВАННЯ ВЕКТОРІВ Перша група аксіом описує відображення j1: Операція додавання векторів задовольняє наступним аксіомам: 1/ Додавання векторів комутативне: для довільних двох векторів
2/ Додавання векторів асоціативне: для " трьох векторів ( (( 3/ Існує такий вектор (для " 4/ Для " вектора (для " Вектор 1.2 АКСІОМИ МНОЖЕННЯ ВЕКТОРА НА ДІЙСНЕ ЧИСЛО Друга група аксіом описує відображення j2: 1/ Операція j2 дистрибутивна відносно додавання векторів: для " векторів l( (для " 2/ Операція j2 дистрибутивна відносно додавання чисел: для " вектора (l+m) (для " 3/ Операція асоціативна: для довільного вектора (для " 4/ Операція множення вектора 1´ Аксіоми 1-2 дозволяють визначити поняття векторного простору. Векторним простором над полем дійсних чисел Векторний простір є математичною структурою ( Нагадаємо поняття ізоморфізму векторних просторів
" двох векторів
Із означення випливає, що 1/ тотожне відображення Перш ніж перейти до формулювання аксіом розмірності нагадаємо ряд понять із курсу алгебри. Система векторів Вектор l1 У випадку лінійної залежності системи векторів x1,x2,...,xk нульовий вектор може бути представлений у вигляді нетривіальної комбінації векто-рів, у випадку ж лінійної незалежності - тільки у вигляді тривіальної. АКСІОМИ РОЗМІРНОСТІ. 1. Існують три лінійно незалежних вектори l1 2. Будь-які чотири вектори (для довільних (l1 ( Аксіоми 1-3 дозволяють ввести поняття тривимірного простору. Векторний простір Щоб одержати аксіоматику n-вимірного векторного простору над полем 1´. Існує n лінійно незалежних векторів: 2´. Будь-яка система. що містить n+1 вектор лінійно залежна. Множина Кожна система n лінійно незалежних векторів простору 1.4 АКСІОМИ СКАЛЯРНОГО ДОБУТКУ ВЕКТОРІВ. Четверта група аксіом описує відображення j3: 2/ Скалярний добуток векторів лінійний: для " трьох векторів дійсних чисел l,m виконується рівність ( (для "
|
|||||||||
|
Последнее изменение этой страницы: 2016-07-11; просмотров: 892; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.135.224 (0.115 с.) |
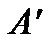 — точка на тій же прямій або на іншій прямій
— точка на тій же прямій або на іншій прямій  , то завжди можна знайти точку
, то завжди можна знайти точку  , що лежить по одну від точки
, що лежить по одну від точки  .
. є відрізками тієї ж прямої чи іншої прямої
є відрізками тієї ж прямої чи іншої прямої  , то й
, то й 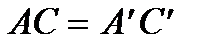 .
. , то в них
, то в них  ,
,  .
. з яких кожний наступний міститься всередині попереднього і, крім того, для довільного відрізка CD існує натуральне число п, таке, що
з яких кожний наступний міститься всередині попереднього і, крім того, для довільного відрізка CD існує натуральне число п, таке, що  . Тоді на прямій а існує точка М, яка належит кожному з відрізків даної послідовності.
. Тоді на прямій а існує точка М, яка належит кожному з відрізків даної послідовності. для будь-якого п, що суперечить аксіомі.
для будь-якого п, що суперечить аксіомі. на два класи К 1 і К 2 (тобто
на два класи К 1 і К 2 (тобто  ), що задовольняє двом умовам:
), що задовольняє двом умовам: і класи К 1 і К 2 містять точки, відмінні від точок А і В;
і класи К 1 і К 2 містять точки, відмінні від точок А і В;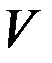 ´
´  ,
,  третій вектор j1(
третій вектор j1( справедлива рівність:
справедлива рівність: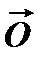 , що для " вектора
, що для " вектора  ) (
) ( ®
®  векторного простору V на векторний простір
векторного простору V на векторний простір 1,
1, 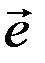 2,
2,  3:
3: ,
,  ,
,  ,
, 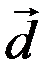 лінійно залежні:
лінійно залежні: ),
), ¹
¹ 


