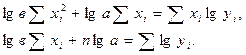Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Обробка й аналіз дослідницького матеріалу
Вважається, що лише тоді науково-дослідна робота починає набувати довершеності, коли її результати вдається перекласти на мову цифр. Ось чому при проведенні досліджень велику роль відіграє математично-статистична обробка й аналіз отриманих даних. Як би упереджено не ставився дослідник до використання методів математичної статистики, та все ж існує межа, нижче якої опускатися не можна. Як мінімум, три речі він повинен назвати: 1) середню величину (чи інший так званий показник положення); 2) середнє квадратичне відхилення (чи інший показник розсіювання); і 3) кількість досліджуваних. Без них його публікація наукової цінності мати не буде. Отже є серйозна підстава цей підрозділ розкрити досить докладно. Візьмемо для цього за основу інформацію, викладену в роботі О.Ф.Артюшенка і А.С.Погрібного зі співавторами[85], інтерпретуючи і доповнюючи її. Слід зауважити, що в проведенні наукових досліджень взагалі і в області фізичного виховання зокрема важливу роль відіграє вибірковий метод. При вибіркових дослідженнях певного показника отримують ряд чисел, які називають вибірковою сукупністю або вибіркою. Сукупність же всіх значень, які можна було б одержати в цьому дослідженні, називається генеральною вибіркою. Судження про те, чи можна поширювати висновки досліджуваної вибірки на всю генеральну сукупність, дає змогу зробити статистичний аналіз.
де n – об’єм вибірки; х і – значення окремих варіант; Sхі – сума всіх значень хі. Для кращого розуміння змісту цього статистичного параметра наведемо приклад. Припустимо, що ми вирішили перевірити рівень фізичної підготовленості учнів двох класів, де роботу проводять різні вчителі фізичної культури. Хай це будуть учні 10-х класів. Для перевірки використаємо вправу-тест: із вису на високій перекладині піднімання ніг до торкання ступнями її грифу. В обох класах опротестовано по 20 юнаків і середні арифметичні значення досліджуваного показника виявилися однаковими – 12 разів.
На перший погляд, можна стверджувати, що учні обох класів підготовлені однаково. Та виявляється, що це не так. В одному класі всі значення досліджуваного показника знаходяться в діапазоні від 10 до 14 разів, а в другому – від 2 до 22 разів. Тобто рівень підготовленості учнів у першому випадку набагато кращий (усі підготовлені приблизно однаково), ніж в другому, де середнє арифметичне значення показника забезпечили декілька відмінно підготовлених учнів, тоді як клас у цілому підготовлений слабко. Отже, окрім середньої арифметичної величини, обов’язково слід визначати і параметри розсіювання значень досліджуваних показників.
 Дисперсія – D складає середню арифметичну з квадратів відхилень окремих варіант хі від їх середньої Вона обчислюється за формулою: Дисперсія – D складає середню арифметичну з квадратів відхилень окремих варіант хі від їх середньої Вона обчислюється за формулою:
Якщо число вимірювань менше 30, використовують формулу:
Із характеристик варіативності ряду найбільш часто використовується середнє квадратичне відхилення - s (сигма), яке є додатнім значенням кореня квадратного зі значення дисперсії.
Дисперсія і середнє квадратичне відхилення – величини абсолютні, вони виражаються у тих же одиницях вимірювання, що і результати вимірювання. А коли виникає необхідність порівняти мінливість двох і більше сукупностей, які виражаються різними одиницями вимірювання, користуються відносними показниками варіації. Одним із таких показників є коефіцієнт варіації – Сv. Цей показник визначається як процентне відношення середнього квадратичного відхилення до середнього арифметичного:
Вибір статистичних характеристик значною мірою визначається законом розподілу результатів вимірювань. При аналізі розподілу результатів вимірювань завжди роблять припущення про той розподіл, який би мала вибірка, коли б число вимірювань було дуже великим. Такий розподіл називають розподілом генеральної сукупності або теоретичним, тоді як розподіл експериментального ряду вимірювань – емпіричним.
Теоретичний розподіл більшості результатів вимірювань описується формулою нормального розподілу: де p і е – математичні константи (p = 3,141, е = 2,7183);
х – результат вимірювань; f(х) – функція густини розподілу. При відображенні в прямокутній системі координат графіка функції нормального розподілу отримується симетрична, “дзвоноподібна” (нормальна) крива. Закон нормального розподілу має в теорії ймовірності, на якій ґрунтується математична статистика, виключно важливе значення. Обробка результатів досліджень у припущенні, що вони розподілені за нормальним законом, легко доводиться до кінця за допомогою простих правил операцій з нормально розподіленими величинами. Більше того, виявляється, що закон розподілу суми незалежних величин при досить широких припущеннях про закони розподілу окремих складових прагне до нормального закону, якщо число складових необмежено збільшується. Суворе доведення цього твердження було дане видатним російським математиком О.Л. Ляпуновим в 1901 р. у так званій центральній граничній теоремі. Суть цієї теореми полягає в тому, що при деяких загальних умовах сума n незалежних випадкових величин, заданих довільними розподілами, має розподіл, який із збільшенням числа n прагне до нормального. Деяка конкретизація означених загальних умов дозволяє так сформулювати теорему Ляпунова. Якщо мається n незалежних величин х1, х2,..., хі,..., хn З математичними очікуваннями а1, а2,..., аі,..., аn і з дисперсіями D (х1), D (х2),..., D (хі),..., D (хn), причому відхилення від їх математичних очікувань (математичне очікування – це більш повна інтерпретація середньої арифметичної величини) не перевищують за абсолютною величиною одного і того ж числа d > 0: |хі - аі| £ s, а всі дисперсії обмежені одним і тим же числом С:
то при достатньо великому n сума випадкових величин хі, тобто буде підпорядкована закону розподілу, як завгодно близькому до закону нормального розподілу. Зрозуміло, що при вибіркових дослідженнях величина n мала, а тому в емпіричних розподілах мають місце певні відхилення від нормального розподілу. Так, для багатьох емпіричних розподілів характерним є зсув кривої вліво або вправо. В зв’язку з цим розрізняють лівосторонню і правосторонню асиметрію. Асиметричність кривої характеризують коефіцієнтом асиметрії – Аs, який розраховують за формулою:
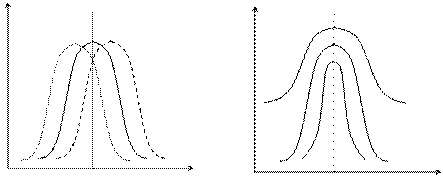
Якщо знак коефіцієнта асиметрії додатний, асиметрія правостороння, якщо від’ємний – лівостороння (рис. 6, а).
Якщо знак ексцесу додатний, то є тенденція до гостровершинності, а при плосковершинності коефіцієнт Ех має від’ємний знак (рис. 6, б). Показники асиметрії та ексцесу дозволяють наближено оцінювати нормальність розподілу. Можна вважати закон розподілу нормальним, якщо значення Аs і Ех в 2-3 рази менші від значень допоміжних коефіцієнтів:
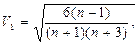
Значення показників асиметрії і ексцесу можна оцінити за допомогою спеціальних таблиць, в яких представлені критичні значення Аs і Ех для різних рівнів значимості і числа спостережень (n). Якщо розраховані значення Аs і Ех не перевищують відповідних критичних значень, роблять висновок про нормальність розподілу отриманих результатів. Підтвердження гіпотези про нормальний розподіл експериментального ряду вимірювань дає підстави поширювати результати досліджуваної вибірки на генеральну сукупність. При цьому зменшується ступінь ризику використати неправильний статистичний метод аналізу. Розв’язання тієї чи іншої задачі не обходиться без порівнянь. Доводиться порівнювати дані дослідження з контролем, результати тестування однієї групи спортсменів з результатами другої, функціональні можливості людей різних вікових груп і т.д. Якщо дані двох порівнюваних вибірок не перекриваються між собою, то є впевненість, що маємо справу з достовірно різними вибірками, а коли ж перекриваються, то достовірність відмінностей не є очевидною. Так, наприклад, під час дослідження рівня фізичної підготовленості учнів двох восьмих класів (використовувався тест в підтягуванні на високій перекладині) було виявлено, що учні 8 а класу підтягувалися в середньому 6 разів з розмахом показників від 4 до 8, а учні 8 б класу підтягувалися в середньому 12 разів з розмахом показників від 9 до 15. Тут не може бути сумнівів в кращій підготовці учнів 8 б класу. А коли б, скажімо, були отримані такі дані: 8 а клас - = 8 разів, розмах 2-14 разів; 8 б клас - = 10 разів, розмах – 3-17 разів, то не можна було б з впевненістю стверджувати, що учні 8 б класу підготовлені краще. В такому і подібних до нього випадках для оцінки достовірності відмінностей показників досліджуваних вибірок, перевірки гіпотези про випадковий характер цих відмінностей (нульової гіпотези) використовують статистичні критерії.
Статистичні критерії забезпечують прийняття або відхилення нульової гіпотези з наперед заданою імовірністю. Так, в дослідницькій роботі приймаються 5 %-й, 1 %-й, та найбільш високий 0,1 %-вий рівні значимості, яким відповідають імовірності р = 0,05; р = 0,01; р = 0,001. Наприклад, якщо виявиться, що р ³ 0,05, нульова гіпотеза зберігається, відкидати її на 5 %-вому рівні значимості немає підстав. Це означає, що різниця, яка спостерігається між вибірковими показниками, випадкова. Якщо ж р < 0,05, нульова гіпотеза відкидається, отже з імовірністю р > 0,95 різниця між вибірковими показниками вважається статистично значимою, або достовірною. Критерії значимості поділяються на параметричні і непараметричні. Якщо результати вимірювань підлягають нормальному розподілу, то для оцінки відмінностей вибіркових показників використовуються параметричні критерії, такі як t-критерій Стьюдента і F-критерій Фішера. При інших формах розподілу використовується ряд непараметричних критеріїв: Х-критерій Ван-дер-Вардена, Т-критерій Уайта, W-критерій Вілкоксона і інші. Бажаючі можуть познайомитися з ними в літературі із статистики.
1.
2. Визначають число ступенів вільності: k = n1 + n2 – 2. 3. Із таблиці розподілу Стьюдента (її завжди можна знайти в літературі із статистики) визначають критичне значення t-критерію для найнижчого рівня значимості р = 0,05 і одержаного значення k. 4. Якщо розраховане значення t-критерію більше від його табличного критичного значення, роблять висновок про достовірність різниці між середніми арифметичними, в іншому випадку підтверджують її недостовірність, тобто випадковість. В фізкультурно-спортивній практиці досить часто виникають завдання, коли необхідно не просто порівняти між собою досліджувані вибірки, а оцінити ступінь взаємозв’язку між досліджуваними перемінними. Наприклад, необхідно підібрати найбільш вдалі тести для контролю спеціальної тренованості спринтера. Існують, скажімо, такі тестові завдання: 1. стрибок в довжину з місця; 2. стрибок у висоту з місця; 3. реагування на слуховий подразник; 4. біг на 30 м; 5. біг на протязі 6 секунд з реєстрацією довжини подоланої дистанції; 6. згинання рук в упорі лежачи на кількість разів; 7. присідання на одній нозі на кількість разів. Досвід показує, що результати 6-го і 7-го тестів дуже слабо пов’язані з результатами бігу на 100 м і для контролю спеціальної тренованості спринтера вони непридатні. А ось результати всіх інших тестів пов’язані з результатами бігу на 100 м. Логічно припустити, що найціннішими будуть ті із них, де такий зв’язок найбільший. Отже, треба оцінити його. Але як? Роблять це шляхом обчислення коефіцієнта кореляції – r. Термін “кореляція” вказує на нестрогу, неоднозначну відповідність між перемінними, як то спостерігається у випадку функціональних зв’язків, коли, наприклад, кожному значенню показника х відповідає тільки одне значення показника у. У випадках, коли одному значенню одного показника відповідає декілька значень другого, говорять про статистичний або кореляційний зв’язок.
Строго кажучи, в природі існують лише кореляційні зв’язки. Навіть в тих явищах, що вивчаються фізикою, хімією, астрономією, взаємозв’язки не ідеально однозначні, але варіації тут настільки мізерні, що їх (взаємозв’язки) можна розглядати як функціональні. Розраховують коефіцієнт кореляції за такою формулою:
Абсолютне значення коефіцієнта кореляції лежить в межах від 0 до 1. Інтерпретують значення цього коефіцієнта так: r = 1,00 (функціональний зв’язок); r = 0,99-0,70 (сильний статистичний зв’язок); r = 0,69-0,50 (середній статистичний зв’язок); r = 0,49-0,20 (слабкий статистичний зв’язок); r = 0,19-0,09 (дуже слабкий статистичний зв’язок); r = 0,00 (кореляції немає). При прямому зв’язку, коли більшим значенням одного показника відповідають більші значення другого r буде з додатнім (+) знаком, а при оберненому зв’язку, коли більшим значенням одного показника відповідають менші значення другого, r буде з від’ємним (-) знаком.
Оцінка достовірності коефіцієнта кореляції проводиться на основі t-критерію, який розраховується за формулою: Розраховане значення t-критерію Стьюдента порівнюють з критичним значенням цього показника, що міститься в спеціальній таблиці. В цьому разі число ступенів вільності на два менше від числа досліджуваних (k=n-2). Якщо одержане значення t-критерію більше за критичне, роблять висновок про існування статистичної залежності, в протилежному випадку приймають r = 0. Значимість, або достовірність можна виявити також, користуючись іншою таблицею (таблицею критичних значень коефіцієнта кореляції). Нульова гіпотеза (відсутність взаємозв’язку, r = 0) відкидається, якщо емпіричний коефіцієнт кореляції перевищує вказану в таблиці величину і число ступенів вільності. Статистичну обробку експериментальних даних виконують, як правило, з використанням обчислювальної техніки за спеціально розробленими для цього програмами, які являють собою певні алгоритми вводу фактичних даних в обчислювальний пристрій, з метою отримання потрібних статистичних параметрів. Отриману в результаті статистичної обробки даних інформацію найчастіше оформлюють у вигляді таблиць, діаграм, схем, графіків. Але бувають випадки, коли залежність між перемінними доцільно виразити аналітично, тобто дати формулу, що пов’язує між собою відповідні значення перемінних. Така формула дуже полегшує аналіз залежності, що вивчається. Формули, що служать для аналітичної ілюстрації дослідних даних називають емпіричними формулами. Треба мати на увазі, підбором емпіричних формул за даними досліджень не можна ставити перед собою завдання розгадати істинний характер залежності між перемінними. Навіть в тому випадку, коли в нашому розпорядженні є точні значення аргументу і функції, відновити функцію за конечним числом її значень – задача математично нерозв’язна. Тим більше не слід сподіватися, що це вдасться зробити, виходячи із експериментальних даних, які обов’язково містять помилки вимірювань чи статистичних спостережень. Найчастіше при підборі емпіричних формул користуються способом найменших квадратів, який ґрунтується на тому, що з даної множини формул виду у = f(x) найкращою вважається та, для якої сума квадратів відхилень досліджуваних значень від обчислених є найменшою. Викладемо ідею даного способу, обмежившись випадком лінійної залежності двох величин. Нехай ми хочемо встановити залежність між двома величинами х і у. Робимо відповідні виміри (наприклад, n вимірів) і результати співставляємо в таблиці:
Природно в цьому випадку вважати, що між х і у існує наближена до лінійної залежність, тобто, що у є лінійна функція від х, яка виражається формулою: у = ах + в, (1) де а і в – деякі постійні коефіцієнти, які належить визначити. Формула (1) може бути представлена в такому вигляді: ах + ву = 0. (2) Так як точки (х, у) тільки наближено лежать на прямій, то формули (1) і (2) наближені. Отже, підставляючи в формулу (2) замість х і у їх значення х1, у1; х2, у2; ...; хn, yn, взяті із таблиці ми отримаємо рівняння:
ах2 + в – у2 = Е2 .......................... (3) ахn + в – уn = Еn де Е1, Е2,..., Еn (4) - деякі числа, загалом кажучи, не рівні нулю, які ми будемо називати погрішностями. Спосіб найменших квадратів полягає в слідуючому: треба підібрати коефіцієнти а і в так, щоб сума квадратів погрішностей була якомога меншою, тобто поставимо вимогу, щоб сума S = Е12 + Е22 +... + Еn 2 (5) була найменшою. Заміняючи у виразі (5) числа (4) їх значеннями із рівнянь (3) отримаємо такий вираз: S = (ax1 + в – у1)2 + (ax2 + в – у2)2 +... + (axn + в – уn)2.
Представимо його в такому вигляді: S можна розглядати як функцію від двох перемінних а і в. Треба підібрати коефіцієнти а і в так, щоб функція S отримала найменше значення, тобто маємо задачу на екстремум. Функція ж має екстремум тоді, коли її часткові похідні рівняються нулю, а саме:
Знаходимо часткові похідні:
Прирівнюючи кожну часткову похідну до нуля, отримуємо систему двох лінійних рівнянь відносно а і в
аS хі + вn = S уі (так звану нормальну систему). Покажемо, як нею користуватися.
Вважаючи, що х і у пов’язані залежністю виду у = ах + в, визначаємо способом найменших квадратів значення а і в. Для складання системи нормальних рівнянь виконаємо необхідні підсумовування за таблицею підрахунків.
Табличні дані приводять до системи
21 + 6в = 13 рішення цієї системи дає значення коефіцієнтів: а» - 5,06 і в» 19,87. І, таким чином, шукана залежність між х і у наближено виражається у вигляді: у = - 5,06х + 19,87. При нелінійній залежності між досліджуваними величинами х і у точки з відповідними координатами, що відповідають експериментальним даним, розміщуються приблизно на якійсь кривій, що дуже часто наближається до графіка або квадратичної функції виду у = ах2 + вх + с, або гіперболи виду у = а + в/х, або показові функції виду у = авх. Наведемо нормальні системи рівнянь для названих функцій. Процедури користування ними аналогічні тим, що наведені стосовно лінійної функції виду у = ах + в.
аS хі4 + вS хі3 + сS хі2 = S хі2 уі, аS хі3 + вS хі2 + сS хі = S хі уі, аS хі2 + вS хі + сn = S уі.
І, нарешті, нормальна система рівнянь для показової функції виду у = авх записується так:
В багатьох випадках за даними досліджень, представленими таблицею значень х і у
безпосередньо не може бути встановлено, якого виду функція f(x) дає можливість заміни табличного представлення аналітичним виразом залежності між х і у. При цьому виключається можливість використання способу найменших квадратів. В таких випадках будують так звані інтерполяційні формули. Бажаючих познайомитись з цим методом відсилаємо до спеціальної літератури із статистики, зокрема до посібника Е.С. Марковича[86].
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 211; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.143.4.181 (0.086 с.) |
 Однією з основних характеристик вибірки є її об’єм – n, який визначається числом об’єктів спостереження в даному дослідженні. До основних статистичних характеристик ряду вимірювань відносять також середнє арифметичне значення яке відображає центральну тенденцію вибірки, а також дисперсію D, середнє квадратичне відхилення - s, похибку середнього арифметичного – SX та коефіцієнт варіації – Сv, які визначають варіативність вибірки.
Однією з основних характеристик вибірки є її об’єм – n, який визначається числом об’єктів спостереження в даному дослідженні. До основних статистичних характеристик ряду вимірювань відносять також середнє арифметичне значення яке відображає центральну тенденцію вибірки, а також дисперсію D, середнє квадратичне відхилення - s, похибку середнього арифметичного – SX та коефіцієнт варіації – Сv, які визначають варіативність вибірки.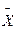 Середнє арифметичне значення – X ряду величин (для генеральної вибірки - М) являє собою центр розподілу, навколо якого групуються всі варіанти статистичної сукупності. Визначається середнє арифметичне за формулою:
Середнє арифметичне значення – X ряду величин (для генеральної вибірки - М) являє собою центр розподілу, навколо якого групуються всі варіанти статистичної сукупності. Визначається середнє арифметичне за формулою: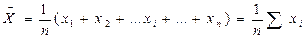
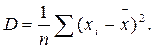
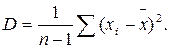
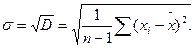
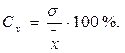
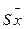 Слід відзначити ще один важливий показник розсіювання – похибку середнього арифметичного – (для генеральної вибірки - m), який характеризує коливання середнього арифметичного. Похибка середнього арифметичного обчислюється за формулою:
Слід відзначити ще один важливий показник розсіювання – похибку середнього арифметичного – (для генеральної вибірки - m), який характеризує коливання середнього арифметичного. Похибка середнього арифметичного обчислюється за формулою: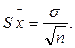
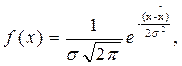
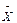 , s - відповідно середнє арифметичне і середнє квадратичне відхилення;
, s - відповідно середнє арифметичне і середнє квадратичне відхилення;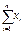 D (хі) £ С,
D (хі) £ С,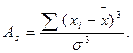
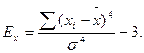 Крім асиметричності криві розподілу мають характеристики плосковершинності та гостровершинності. Їх характеризують величиною ексцесу, яку знаходять за формулою:
Крім асиметричності криві розподілу мають характеристики плосковершинності та гостровершинності. Їх характеризують величиною ексцесу, яку знаходять за формулою: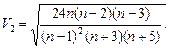
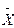
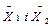 Перевірку достовірності різниці двох вибіркових середніх за допомогою t-критерію виконують так.
Перевірку достовірності різниці двох вибіркових середніх за допомогою t-критерію виконують так. Розраховують значення t-критерію за формулою:
Розраховують значення t-критерію за формулою: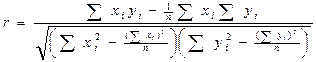
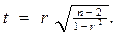
 х
х

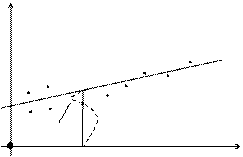 Будемо розглядати х і у як прямокутні координати точок на площині. Припустимо, що точки з відповідними координатами, взятими з нашої таблиці, майже лежать на деякій прямій лінії, як це показано на рисунку.
Будемо розглядати х і у як прямокутні координати точок на площині. Припустимо, що точки з відповідними координатами, взятими з нашої таблиці, майже лежать на деякій прямій лінії, як це показано на рисунку. ах1 + в – у1 = Е1
ах1 + в – у1 = Е1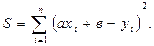
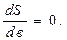
 і
і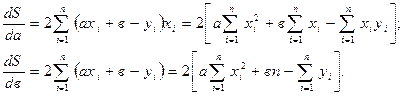
 аS хі2 + вS хі = S хіуі
аS хі2 + вS хі = S хіуі Маємо, наприклад, деякі дослідні дані про значення х і у представлені таблицею
Маємо, наприклад, деякі дослідні дані про значення х і у представлені таблицею 91а + 21в = - 43
91а + 21в = - 43 Отже, стосовно квадратичної функції виду у = ах2 + вх + с нормальна система рівнянь має такий вигляд:
Отже, стосовно квадратичної функції виду у = ах2 + вх + с нормальна система рівнянь має такий вигляд: Для функції виду у = а + в/х такий:
Для функції виду у = а + в/х такий: