Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Производная функции, заданной неявно
Дифференцирование функций, заданных неявно, опирается на возможность почленного дифференцирования тождеств. В общем случае уравнение почленно дифференцировать нельзя. Пусть функция Продифференцировав
Пример Найти производную функции, заданной неявно: Решение Продифференцируем обе части данного уравнения по аргументу х:
Дифференцирование функций, заданных параметрически
Пусть функция (1) Требуется найти производную Имеет место формула
Пример Найти производную функции, заданной параметрически: Решение Найдем производные функций х и у по переменной t:
Согласно формуле
Исследование функций и построение графиков функций Одна из возможных схем исследования функции и построения ее графика включает следующие этапы решения задачи:
1. Найти область определения функции. 2. Найти точки пересечения графика функции с осями координат. 3. Определить четность, нечетность, периодичность функции. 4. Исследовать функцию на экстремум, найти интервалы монотонности функции, точки максимума и минимума. 5. Найти интервалы выпуклости, вогнутости графика функции и точки перегиба. 6. Найти точки разрыва функции и асимптоты графика функции. 7. Построить график функции.
Пример С помощью методов дифференциального исчисления исследовать и построить график функции Решение 1. Область определения функции находится из условия: 2. Точки пересечения графика функции с осями координат: с осью Оу, с осью Ох, 3. Четность, нечетность, периодичность функции. Функция В нашем случае,
Функция непериодическая. 4. Исследование функции на экстремум. Для определения интервалов возрастания и убывания функции и ее точек экстремума найдем первую производную:
Найдем критические точки, т.е. точки, в которых производная равна нулю или не существует, для чего приравниваем числитель
5. Исследование на выпуклость, вогнутость. Точки перегиба. Вычислим производную второго порядка:
_ + _ +
Так как при переходе через точку
6. Точки разрыва функции и асимптоты графика функции. 1) Вертикальные асимптоты. Прямая
равен Заданная функция имеет две точки разрыва второго рода
следовательно, график функции имеет две вертикальных асимптоты 2) Наклонные асимптоты. Пусть прямая
Аналогично находится асимптота при Так как 3) Горизонтальные асимптоты. Горизонтальная асимптота – частный случай наклонной асимптоты, когда Чтобы найти горизонтальные асимптоты графика функции, нужно найти пределы:
Если эти пределы конечны и различны, то прямые
Так как
то график функции имеет горизонтальную асимптоту
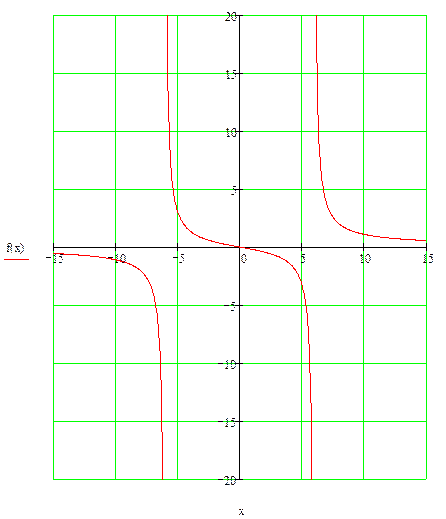
7. Построение графика функции.
Для уточнения построения графика функции можно найти ряд вспомогательных точек
после чего строим график функции.
|
|||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-21; просмотров: 402; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.166.98 (0.016 с.) |
 задана неявно уравнением
задана неявно уравнением  и известно, что существует решение этого уравнения в виде
и известно, что существует решение этого уравнения в виде  .
. .
. .
.
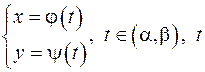 - параметр.
- параметр. .
. или
или  .
. .
. ,
, .
. .
. .
. , т.е.
, т.е.  .
. , точка
, точка  ,
, , точка
, точка  называется четной, если для любого х из области определения справедливо равенство
называется четной, если для любого х из области определения справедливо равенство  . Функция
. Функция 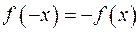 . Если не выполнено ни одно из равенств, то функцию называют функцией общего вида.
. Если не выполнено ни одно из равенств, то функцию называют функцией общего вида.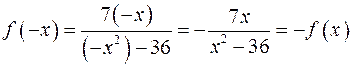 , следовательно, функция нечетная, а ее график симметричен относительно начала координат.
, следовательно, функция нечетная, а ее график симметричен относительно начала координат. .
.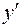 к нулю:
к нулю: , т.е. вещественных корней нет, следовательно, точек экстремума нет. Так как производная отрицательна во всей области определения функции, то она всюду убывает в этой области.
, т.е. вещественных корней нет, следовательно, точек экстремума нет. Так как производная отрицательна во всей области определения функции, то она всюду убывает в этой области.

 _ _ _
_ _ _ 

 х
х

 -6 6 у
-6 6 у Необходимое условие точки перегиба:
Необходимое условие точки перегиба:  или не существует. Равенство
или не существует. Равенство  выполняется при
выполняется при  , следовательно, эта точка является «подозрительной» на точку перегиба. Определим знак второй производной на всей числовой оси и укажем на ней интервалы выпуклости и вогнутости функции.
, следовательно, эта точка является «подозрительной» на точку перегиба. Определим знак второй производной на всей числовой оси и укажем на ней интервалы выпуклости и вогнутости функции.




 х
х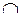 -6
-6  0
0  является вертикальной асимптотой графика функции
является вертикальной асимптотой графика функции  или
или 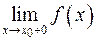
 или
или  . Таким образом, для нахождения вертикальных асимптот следует найти все точки разрыва 2-го рода данной функции. Если точек разрыва нет, то нет и вертикальных асимптот.
. Таким образом, для нахождения вертикальных асимптот следует найти все точки разрыва 2-го рода данной функции. Если точек разрыва нет, то нет и вертикальных асимптот. и
и  , так как
, так как ,
, 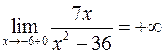 ,
, ,
,  ,
, и
и  .
. является асимптотой графика функции
является асимптотой графика функции  наклонную асимптоту
наклонную асимптоту 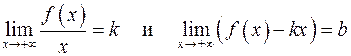 .
. .
. , то наклонных асимптот нет.
, то наклонных асимптот нет.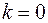 .
. .
. будут горизонтальными асимптотами. Если какой-либо из этих пределов не существует или равен
будут горизонтальными асимптотами. Если какой-либо из этих пределов не существует или равен 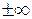 , то не существуют и соответствующие асимптоты.
, то не существуют и соответствующие асимптоты. ,
,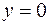 .
.