
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Метод интегрирования по частям
Метод интегрирования по частям следует из формулы дифференцирования произведения двух функций. Если
Последняя формула называется формулой интегрирования по частям. Она сводит вычисление интеграла В таблице приведены типы интегралов, которые могут быть вычислены только по частям, и указано, что следует принимать за u и, что на dv.
где а и b − числа.
Замечание. Иногда, для получения результата надо последовательно применить интегрирование по частям несколько раз.
Примеры 1.
2.
Понятие определенного интеграла
Общий предел всех интегральных сумм функции f (x) на отрезке [ a, b ] называется определенным интегралом от функции f (x) в пределах от a до b и обозначается:
Таким образом,
В этом случае функция f (х) называется интегрируемой на [ a, b ]. Числа a и b называются соответственно нижним и верхним пределами интегрирования, f (х) — подынтегральной функцией, х — переменной интегрирования. Свойства определенного интеграла 1. При перестановке пределов интегрирования меняется знак интеграла:
2. Интеграл с одинаковыми пределами равен нулю:
3. Отрезок интегрирования можно разбивать на части:
4. Определенный интеграл от алгебраической суммы функций равен алгебраической сумме их интегралов, т. е.
5. Постоянный множитель можно выносить за знак определенного интеграла, т. е.
6. Если функции
т.е. неравенство можно интегрировать. 7. Если
8. Теорема о среднем. Если функция
Это равенство называется формулой среднего значения, а величина Геометрический смысл теоремы о среднем: величина определённого интеграла при
Формула Ньютона-Лейбница
Эта формула открывает широкие возможности для вычисления определенных интегралов, поскольку задача вычисления определенного интеграла сводится к задаче вычисления неопределенного интеграла, которая достаточно полно изучена.
Рассмотрим примеры применения формулы Ньютона-Лейбница. 1. 2.
Интегрирование заменой переменной Теорема. Пусть 1) функция 2) множеством значений функции 3) Тогда справедлива формула:
Пример. Вычислить Решение.
Интегрирование по частям Теорема 3. Если функции u (х) и v (х) имеют непрерывные производные на отрезке
Пример 8. Вычислить Решение.
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2022-09-03; просмотров: 38; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.161.228 (0.014 с.) |
 и
и 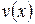 − дифференцируемые функции, то
− дифференцируемые функции, то
 к вычислению интеграла
к вычислению интеграла  , который может оказаться более простым, чем первый.
, который может оказаться более простым, чем первый.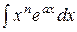
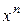
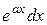
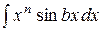
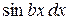



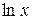

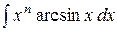


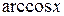
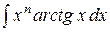
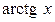
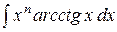
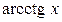

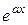

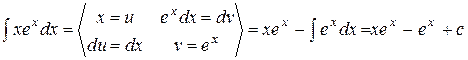 ;
;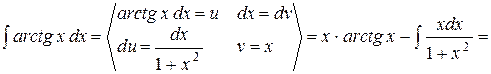
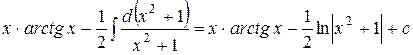 ;
;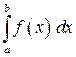 .
.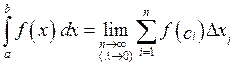
 .
. .
. с Î [ a, b ].
с Î [ a, b ].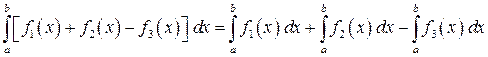 .
.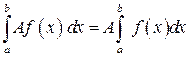 .
.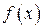 и
и 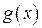 на отрезке
на отрезке 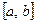 удовлетворяют условию
удовлетворяют условию 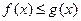 , то
, то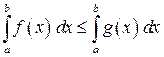 ,
, и
и 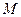 – соответственно наименьшее и наибольшее значения функции
– соответственно наименьшее и наибольшее значения функции 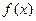 на отрезке
на отрезке  , то
, то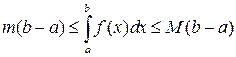 .
.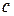 такая, что
такая, что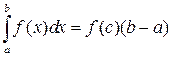 .
.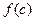 – средним значением функции
– средним значением функции  0 равна площади прямоугольника, имеющего высоту
0 равна площади прямоугольника, имеющего высоту 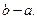
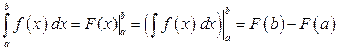
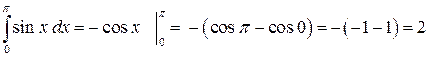 .
. .
.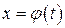 и ее производная
и ее производная  непрерывны при
непрерывны при 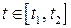 ;
;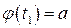 и
и 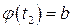 .
. .
. 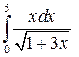 .
.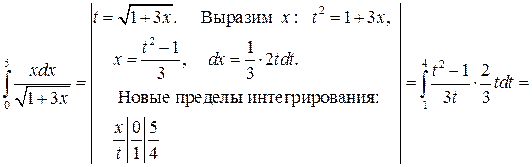
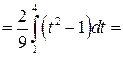
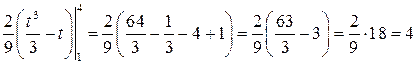 .
.
 .
.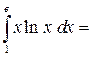
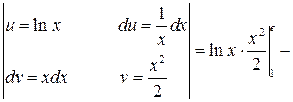

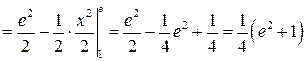 .
.


