
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Государственной противопожарной службы МЧС России»Стр 1 из 5Следующая ⇒
Государственной противопожарной службы МЧС России»
кафедра высшей математики и системного моделирования сложных процессов
МЕТОДИЧЕСКИЕ УКАЗАНИЯ И ЗАДАНИЯ ДЛЯ ВЫПОЛНЕНИЯ РАСЧЁТНО-ГРАФИЧЕСКИХ РАБОТ (КОНТРОЛЬНЫХ РАБОТ) По дисциплине Математика Направлению подготовки 38.03.04 – «Государственное и муниципальное управление»
УДК 517
Методические указания содержат краткие теоретические сведения по темам: «Операторы дифференцирования», «Операторы интегрирования». Предназначены для обучающихся очной формы обучения по направлению подготовки 38.03.04 «Государственное и муниципальное управление». Авторы: кандидат педагогических наук, доцент Е.Н.Трофимец кандидат технических наук, доцент Н.В.Каменецкая кандидат экономических наук, доцент Пекарская О.А.
Дифференциальное исчисление функции одной переменной Расчётно-графическая работа «Операторы дифференцирования»
Определение. Производной функции
Записывают:
Производная функции
Определение. Операция нахождения производной функции называется дифференцированием.
Геометрический смысл производной состоит в том, что значение производной равно тангенсу угла, образованного касательной к графику функции
Производная сложной функции Пусть
Теорема. Если функции
Кратко это можно сформулировать так (правило цепочки): производная сложной функции равна произведению производных от функций ее составляющих.
Определение. Дифференциалом функции
Для функции
Тогда
Значит, дифференциал функции равен произведению ее производной на дифференциал независимой переменной. Из формулы
Следовательно, производная функции равна отношению дифференциала функции к дифференциалу ее аргумента.
Определение. Точка
Значение функции в точке максимума (минимума) называют максимумом (минимумом) функции или экстремумом функции. Из определения следует, что экстремум функции имеет локальный характер. Рассмотрим условия существования экстремума функции.
Теорема (необходимое условие экстремума). Если дифференцируемая функция
Теорема (первое достаточное условие экстремума). Если непрерывная функция
Укажем правило нахождения наибольшего и наименьшего значений функции на отрезке 1) найти критические точки функции на интервале 2) вычислить значения функции в критических точках; 3) вычислить значения функции на концах отрезка 4) среди вычисленных значений функции выбрать наибольшее или наименьшее.
Теорема (второе достаточное условие экстремума) Если в точке Определение. График дифференцируемой функции
Теорема. Если функция
Определение. Точка графика непрерывной функции
Теорема (достаточное условие существования точки перегиба) Если вторая производная
Определение. Прямая
Асимптоты графика функции Вертикальные асимптоты Определение. Асимптотой кривой называется прямая, расстояние до которой от точки, лежащей на кривой, стремится к нулю при неограниченном удалении от начала координат этой точки по кривой (рис.5.10).
Асимптоты бывают вертикальные (параллельные оси Оу), горизонтальные (параллельные оси Ох) и наклонные.
Горизонтальные асимптоты Определение. Если при
то прямая
Наклонные асимптоты Определение. Прямая
Наличие наклонной асимптоты устанавливают с помощью следующей теоремы.
Теорема. Для того, чтобы график функции
Если хотя бы один из этих пределов не существует или равен бесконечности, то кривая
Варианты индивидуальных заданий В задачах 1 – 20 найти производные заданных функций.
1. а) 2. а) 3. а) 4. а) 5. а) 6. а) 7. а) 8. а) 9. а) 10. а) 11. а) 12. а) 13. а) 14. а) 15. а) 16. а) 17. а) 18. а) 19. а) 20. а)
В задачах 1 – 20 найти дифференциалы второго порядка.
1. 4. 7. 10. 13. 16. 19.
В задачах 1 – 20 исследовать данные функции методами дифференциального исчисления и построить их графики.
1. 4. 7. 10. 13. 16. 19.
Расчётно-графическая работа «Операторы интегрирования»
Первообразная функция Основной задачей дифференциального исчисления является нахождение производной от данной функции. Интегральное исчисление решает обратную задачу: найти функцию F (x), зная ее производную
Определение. Функция
Неопределенный интеграл Определение. Совокупность всех первообразных функций
Обозначается:
где
Операция нахождения первообразной для данной функции называется интегрированием этой функции. Дифференцирование и интегрирование функций − это две взаимно обратные операции.
Таблица основных интегралов
Линейные подстановки При сведении данного интеграла к табличному часто используются преобразования дифференциала (операция «подведения под знак дифференциала»). I. Под знак дифференциала, стоящего в интеграле, можно ввести любое постоянное слагаемое. При любой постоянной а будет
Поэтому
Примеры 1.
2.
3.
II. Под знак дифференциала, стоящего в интеграле, можно ввести любой постоянный множитель, разделив на него интеграл. Известно, если а − постоянно, то
Тогда
Поэтому
Примеры 1.
2.
3.
В некоторых случаях применяют оба приема вместе:
где а и b − постоянные.
Примеры
2.
3.
Подстановка вида Правило. Чтобы найти интеграл 1) переписать интеграл в виде
2) сделать замену
3) найти последний интеграл; 4) в полученном ответе произвести обратную замену u на
Примеры 1.
2.
Подстановка вида Правило. Чтобы найти интеграл 1) перейти к новой переменной t, связанной с х выражением 2) выразить через t все подынтегральное выражение
3) найти новый интеграл:
4) в полученном ответе произвести обратную замену
Примеры 1.
2.
Замечание. Иногда, для получения результата надо последовательно применить интегрирование по частям несколько раз.
Примеры 1.
2.
Формула Ньютона-Лейбница
Эта формула открывает широкие возможности для вычисления определенных интегралов, поскольку задача вычисления определенного интеграла сводится к задаче вычисления неопределенного интеграла, которая достаточно полно изучена.
Рассмотрим примеры применения формулы Ньютона-Лейбница. 1. 2.
Интегрирование по частям Теорема 3. Если функции u (х) и v (х) имеют непрерывные производные на отрезке
Пример 8. Вычислить Решение.
Варианты индивидуальных заданий В задачах 1 – 20 найти неопределенные интегралы.
1. а) 2. а) 3. а) 4. а) 5. а) 6. а) 7. а) 8. а) 9. а) 10. а) 11. а) 12. а) 13. а) 14. а) 15. а) 16. а) 17. а) 18. а) 19. а) 20. а)
В задачах 1 – 20 вычислить определенные интегралы.
1. а) 2. а) 3. а) 4. а) 5. а) 6. а) 7. а) 8. а) 9. а) 10. а) 11. а) 12. а) 13. а) 14. а) 15. а) 16. а) 17. а) 18. а) 19. а) 20. а)
В задачах 1 – 20 найти площади фигуры, ограниченных линиями. Сделать чертеж.
1. 3. 5. 7. 9. 11. 13. 15.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2022-09-03; просмотров: 55; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.14.221.113 (0.247 с.) |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
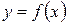 называется предел отношения приращения функции к приращению аргумента, когда приращение аргумента стремится к нулю.
называется предел отношения приращения функции к приращению аргумента, когда приращение аргумента стремится к нулю. или
или 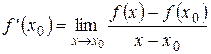 .
.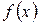 есть некоторая функция
есть некоторая функция 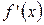 , произведенная из данной функции.
, произведенная из данной функции.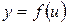 и
и 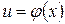 , тогда
, тогда 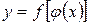 − сложная функция с промежуточным аргументом u и независимым аргументом х.
− сложная функция с промежуточным аргументом u и независимым аргументом х. в точке х, а функция
в точке х, а функция  в соответствующей точке
в соответствующей точке 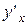 , которая находится по формуле:
, которая находится по формуле: или
или 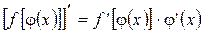 .
.
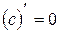 ,
, 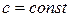


 ,
, 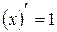
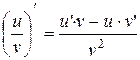 ,
, 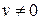 .
.
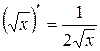
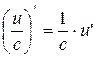 ,
, 
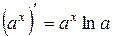
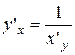 ,
если
,
если 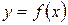 ,
, 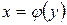
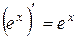
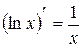
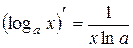
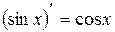
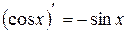
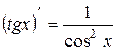
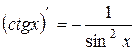
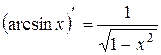
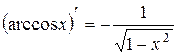

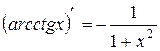
 или
или 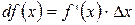 .
.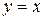 имеем:
имеем: , т.е.
, т.е. 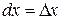 .
. или
или 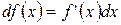 .
. или
или  .
. называется точкой максимума (точкой минимума) функции
называется точкой максимума (точкой минимума) функции 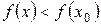
 .
. .
.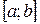 :
: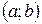 ;
; и
и 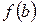 ;
; , а вторая производная в точке
, а вторая производная в точке 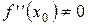 , то при
, то при 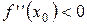 в точке
в точке  .
. , то график функции в этом интервале выпуклый. Если
, то график функции в этом интервале выпуклый. Если  − график вогнутый.
− график вогнутый.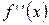 при переходе через точку
при переходе через точку  называется вертикальной асимптотой графика функции
называется вертикальной асимптотой графика функции  или
или  (рис.5.11)
(рис.5.11) (
(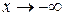 ) функция
) функция 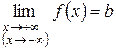 ,
, есть горизонтальная асимптота графика функции
есть горизонтальная асимптота графика функции  называется наклонной асимптотой графика функции
называется наклонной асимптотой графика функции 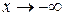 ), если выполняется равенство
), если выполняется равенство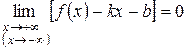 .
.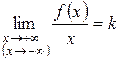 и
и  .
.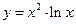 ; б)
; б) 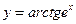 ; в)
; в) 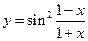 .
.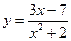 ; б)
; б) 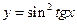 ; в)
; в) 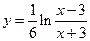 .
.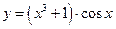 ; б)
; б) 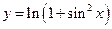 ; в)
; в) 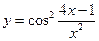 .
.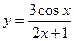 ; б)
; б)  ; в)
; в) 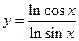 .
.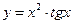 ; б)
; б) 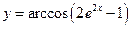 ; в)
; в)  .
.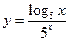 ; б)
; б)  ; в)
; в) 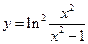 .
.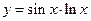 ; б)
; б) 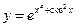 ; в)
; в) 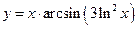 .
.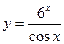 ; б)
; б) 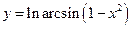 ; в)
; в) 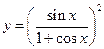 .
.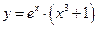 ; б)
; б)  ; в)
; в) 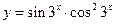 .
.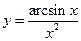 ; б)
; б)  ; в)
; в) 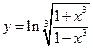 .
.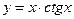 ; б)
; б) 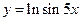 ; в)
; в) 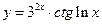 .
.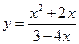 ; б)
; б) 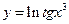 ; в)
; в) 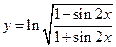 .
. ; б)
; б) 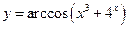 ; в)
; в) 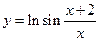 .
.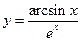 ; б)
; б) 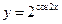 ; в)
; в) 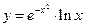 .
.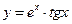 ; б)
; б) 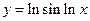 ; в)
; в) 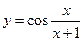 .
.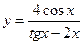 ; б)
; б) 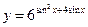 ; в)
; в) 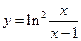 .
. ; б)
; б)  ; в)
; в)  .
. ; б)
; б) 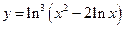 ; в)
; в) 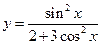 .
. ; б)
; б)  ; в)
; в) 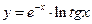 .
. ; б)
; б) 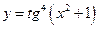 ; в)
; в) 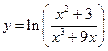 .
.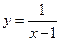 . 2.
. 2. 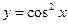 . 3.
. 3. 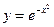 .
. . 5.
. 5. 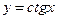 . 6.
. 6. 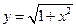 .
.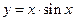 . 9.
. 9. 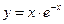 .
.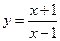 . 11.
. 11. 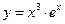 . 12.
. 12. 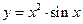 .
.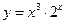 . 14.
. 14.  . 15.
. 15.  .
.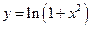 . 17.
. 17.  . 18.
. 18.  .
.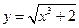 . 20.
. 20. 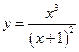 . 2.
. 2. 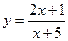 . 3.
. 3. 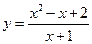 .
.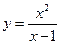 . 5.
. 5. 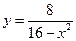 . 6.
. 6. 
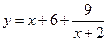 . 8.
. 8. 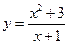 . 9.
. 9. 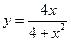 .
. . 11.
. 11.  . 12.
. 12. 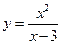 .
.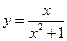 . 14.
. 14.  . 15.
. 15.  .
.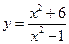 . 17.
. 17. 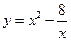 . 18.
. 18. 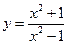 .
.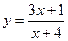 . 20.
. 20.  .
.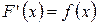 . Искомую функцию называют первообразной функции
. Искомую функцию называют первообразной функции 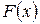 называется первообразной функции
называется первообразной функции  выполняется равенство:
выполняется равенство: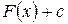 для данной функции
для данной функции 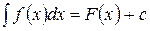 ,
,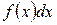 − подынтегральное выражение.
− подынтегральное выражение. ;
;
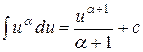
 ;
;
 ;
;
 ;
;
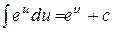 ;
;
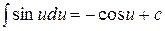 ;
;
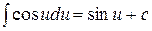 ;
;
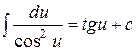 ;
;
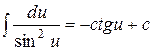 ;
;
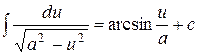 ;
;
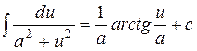 ;
;
 ;
;
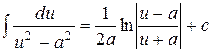 ;
;
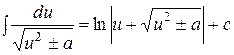 .
.
 .
.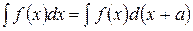 .
.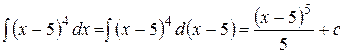 ;
;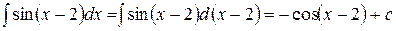 ;
; .
.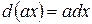 .
.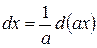 .
. .
.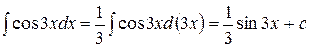 ;
;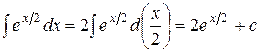 ;
;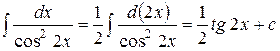 .
.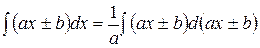 ,
,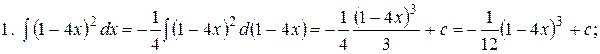
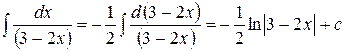 ;
; .
. , надо
, надо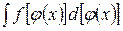 ;
;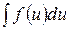 ;
;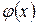 .
.
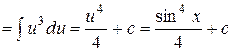 ;
;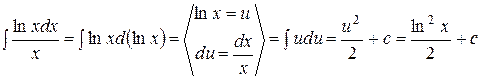 ;
;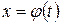
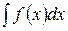 , надо
, надо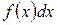 :
: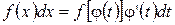 ;
;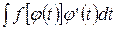 ;
;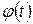 на х.
на х.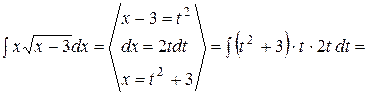
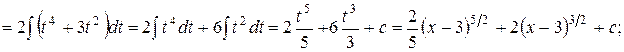
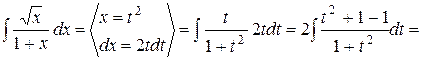
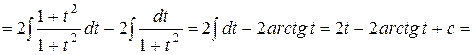
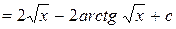 .
.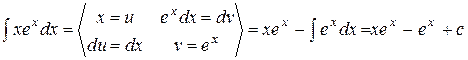 ;
;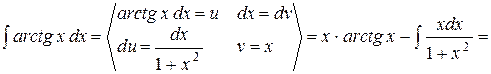
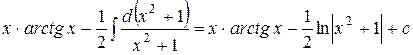 ;
;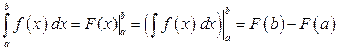
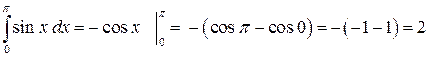 .
. .
.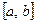 , то справедлива формула
, то справедлива формула
 .
.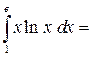
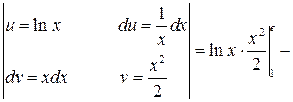

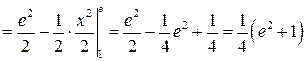 .
. ; б)
; б) 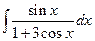 ; в)
; в) 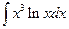 .
. ; б)
; б) 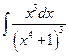 ; в)
; в) 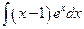 .
.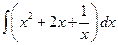 ; б)
; б) 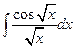 ; в)
; в) 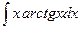 .
.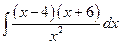 ; б)
; б) 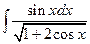 ; в)
; в) 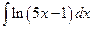
 ; б)
; б) 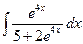 ; в)
; в) 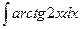 .
. ; б)
; б) 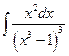 ; в)
; в) 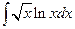 .
.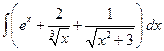 ; б)
; б) 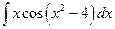 ; в)
; в) 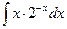 .
. ; б)
; б) 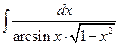 ; в)
; в) 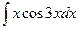 .
.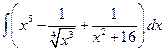 ; б)
; б)  ; в)
; в) 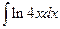 .
.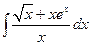 ; б)
; б) 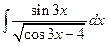 ; в)
; в) 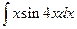 .
.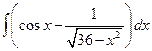 ; б)
; б) 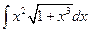 ; в)
; в) 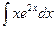 .
.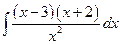 ; б)
; б)  ; в)
; в) 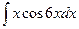 .
.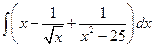 ; б)
; б) 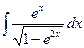 ; в)
; в) 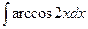 .
. ; б)
; б)  ; в)
; в)  .
. ; б)
; б) 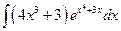 ; в)
; в)  .
. ; б)
; б)  ; в)
; в) 
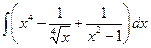 ; б)
; б)  ; в)
; в) 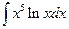 .
. ; б)
; б) 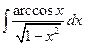 ; в)
; в) 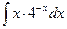 .
. ; б)
; б) 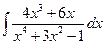 ; в)
; в) 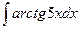 .
.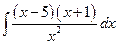 ; б)
; б) 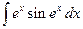 ; в)
; в)  .
.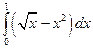 ; б)
; б) 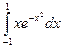 .
. ; б)
; б) 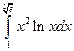 .
.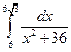 ; б)
; б) 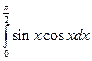 .
.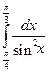 ; б)
; б) 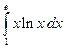 .
.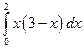 ; б)
; б) 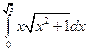 .
.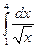 ; б)
; б) 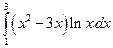 .
. ; б)
; б) 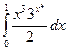 .
.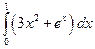 ; б)
; б)  .
. ; б)
; б) 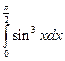 .
. ; б)
; б)  .
.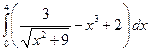 ; б)
; б) 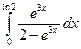 .
. ; б)
; б)  .
.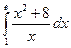 ; б)
; б)  .
. ; б)
; б)  .
. ; б)
; б)  .
.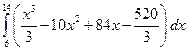 ; б)
; б) 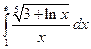 .
. ; б)
; б) 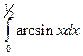 .
.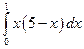 ; б)
; б) 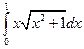 .
.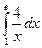 ; б)
; б)  .
.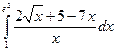 ; б)
; б) 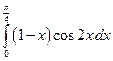 .
. ,
, 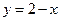 ,
,  . 2.
. 2. 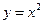 ,
, 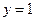 .
.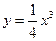 ,
, 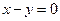 . 4.
. 4. 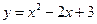 ,
,  .
.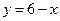 ,
,  ,
, 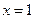 ,
,  ,
, 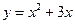 ,
, 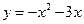
 ,
,  . 10.
. 10. 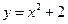 ,
, 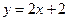 .
.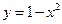 ,
,  ,
, 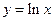 ,
, 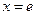 ,
,  . 14.
. 14. 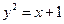 ,
, 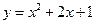 .
.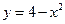 ,
, 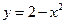 .
.


