
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Общая схема исследования функции и построение графика
Исследование функции 1. Найти область определения функции. 2. Исследовать функцию на четность и нечетность. 3. Исследовать функцию на периодичность. 4. Найти точки пересечения графика функции с осями координат. 5. Найти интервалы знакопостоянства функции (интервалы, на которых 6. Найти асимптоты графика функции. 7. Найти интервалы монотонности и точки экстремума функции. 8. Найти интервалы выпуклости и вогнутости и точки перегиба графика функции. 9. Построить график функции.
Варианты индивидуальных заданий В задачах 1 – 20 найти производные заданных функций.
1. а) 2. а) 3. а) 4. а) 5. а) 6. а) 7. а) 8. а) 9. а) 10. а) 11. а) 12. а) 13. а) 14. а) 15. а) 16. а) 17. а) 18. а) 19. а) 20. а)
В задачах 1 – 20 найти дифференциалы второго порядка.
1. 4. 7. 10. 13. 16. 19.
В задачах 1 – 20 исследовать данные функции методами дифференциального исчисления и построить их графики.
1. 4. 7. 10. 13. 16. 19.
Интегральное исчисление функции одной переменной Расчётно-графическая работа «Операторы интегрирования»
Первообразная функция Основной задачей дифференциального исчисления является нахождение производной от данной функции. Интегральное исчисление решает обратную задачу: найти функцию F (x), зная ее производную
Определение. Функция
Неопределенный интеграл Определение.
Совокупность всех первообразных функций
Обозначается:
где
Операция нахождения первообразной для данной функции называется интегрированием этой функции. Дифференцирование и интегрирование функций − это две взаимно обратные операции.
Свойства неопределенного интеграла Отметим ряд свойств неопределенного интеграла, вытекающих из его определения. 1. Дифференциал от неопределенного интеграла равен подынтегральному выражению:
2. Производная неопределенного интеграла равна подынтегральной функции:
3. Неопределенный интеграл от дифференциала некоторой функции равен сумме этой функции и произвольной постоянной:
4. Постоянный множитель можно выносить за знак интеграла:
5. Неопределенный интеграл от суммы (разности) функций равен сумме (разности) их неопределенных интегралов:
6. Всякая формула интегрирования сохраняет свой вид при подстановке вместо независимой переменной любой дифференцируемой от нее функции. Если
Таблица основных интегралов
Линейные подстановки При сведении данного интеграла к табличному часто используются преобразования дифференциала (операция «подведения под знак дифференциала»). I. Под знак дифференциала, стоящего в интеграле, можно ввести любое постоянное слагаемое. При любой постоянной а будет
Поэтому
Примеры 1.
2.
3.
II. Под знак дифференциала, стоящего в интеграле, можно ввести любой постоянный множитель, разделив на него интеграл. Известно, если а − постоянно, то
Тогда
Поэтому
Примеры 1.
2.
3.
В некоторых случаях применяют оба приема вместе:
где а и b − постоянные.
Примеры
2.
3.
Подстановка вида Правило. Чтобы найти интеграл 1) переписать интеграл в виде
2) сделать замену
3) найти последний интеграл; 4) в полученном ответе произвести обратную замену u на
Примеры 1.
2.
Подстановка вида Правило. Чтобы найти интеграл 1) перейти к новой переменной t, связанной с х выражением 2) выразить через t все подынтегральное выражение
3) найти новый интеграл:
4) в полученном ответе произвести обратную замену
Примеры 1.
2.
|
||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2022-09-03; просмотров: 43; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.128.206.68 (0.083 с.) |
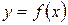 целесообразно проводить по следующей схеме.
целесообразно проводить по следующей схеме.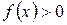 или
или 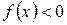 ).
).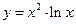 ; б)
; б) 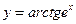 ; в)
; в) 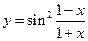 .
.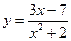 ; б)
; б) 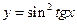 ; в)
; в) 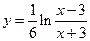 .
.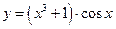 ; б)
; б) 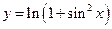 ; в)
; в) 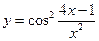 .
.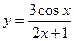 ; б)
; б)  ; в)
; в) 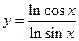 .
.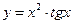 ; б)
; б) 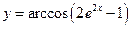 ; в)
; в)  .
.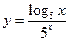 ; б)
; б)  ; в)
; в) 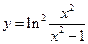 .
.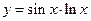 ; б)
; б) 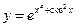 ; в)
; в) 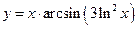 .
.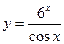 ; б)
; б) 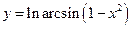 ; в)
; в) 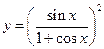 .
.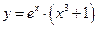 ; б)
; б)  ; в)
; в) 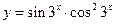 .
.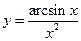 ; б)
; б)  ; в)
; в) 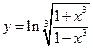 .
.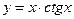 ; б)
; б) 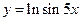 ; в)
; в) 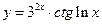 .
.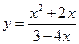 ; б)
; б) 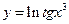 ; в)
; в) 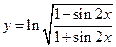 .
. ; б)
; б) 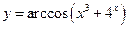 ; в)
; в) 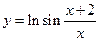 .
.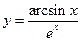 ; б)
; б) 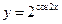 ; в)
; в) 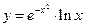 .
.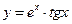 ; б)
; б) 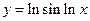 ; в)
; в) 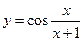 .
.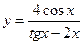 ; б)
; б) 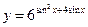 ; в)
; в) 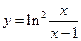 .
. ; б)
; б)  ; в)
; в)  .
. ; б)
; б) 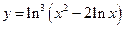 ; в)
; в) 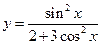 .
. ; б)
; б)  ; в)
; в) 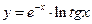 .
. ; б)
; б) 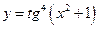 ; в)
; в) 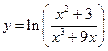 .
.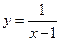 . 2.
. 2. 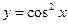 . 3.
. 3. 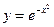 .
. . 5.
. 5. 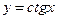 . 6.
. 6. 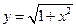 .
.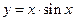 . 9.
. 9. 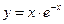 .
.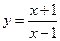 . 11.
. 11. 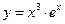 . 12.
. 12. 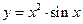 .
.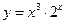 . 14.
. 14.  . 15.
. 15.  .
.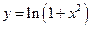 . 17.
. 17.  . 18.
. 18.  .
.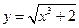 . 20.
. 20. 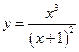 . 2.
. 2. 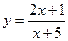 . 3.
. 3. 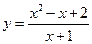 .
.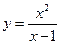 . 5.
. 5. 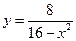 . 6.
. 6. 
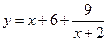 . 8.
. 8. 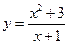 . 9.
. 9. 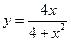 .
. . 11.
. 11.  . 12.
. 12. 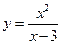 .
.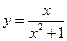 . 14.
. 14.  . 15.
. 15.  .
.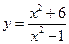 . 17.
. 17. 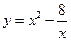 . 18.
. 18. 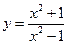 .
.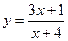 . 20.
. 20.  .
.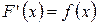 . Искомую функцию называют первообразной функции
. Искомую функцию называют первообразной функции 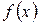 .
.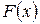 называется первообразной функции
называется первообразной функции 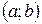 , если для любого
, если для любого  выполняется равенство:
выполняется равенство: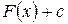 для данной функции
для данной функции 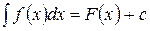 ,
,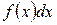 − подынтегральное выражение.
− подынтегральное выражение.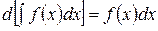 .
.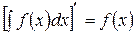 .
. .
.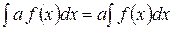 , а − постоянная.
, а − постоянная.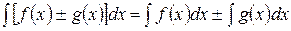 .
.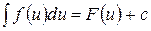 , где
, где 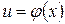 .
. ;
;
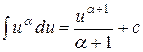
 ;
;
 ;
;
 ;
;
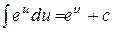 ;
;
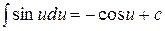 ;
;
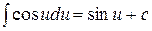 ;
;
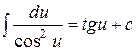 ;
;
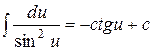 ;
;
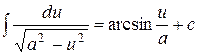 ;
;
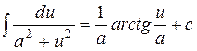 ;
;
 ;
;
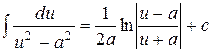 ;
;
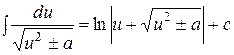 .
.
 .
.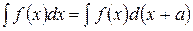 .
.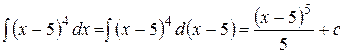 ;
;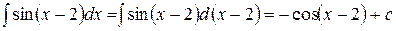 ;
; .
.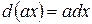 .
.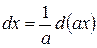 .
. .
.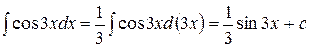 ;
;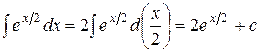 ;
;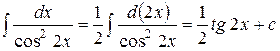 .
.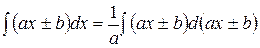 ,
,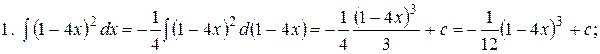
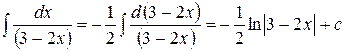 ;
; .
. , надо
, надо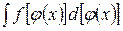 ;
;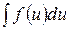 ;
;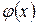 .
.
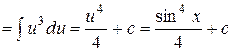 ;
;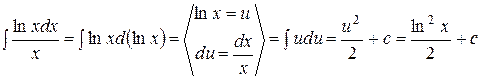 ;
;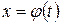
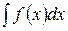 , надо
, надо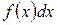 :
: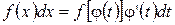 ;
;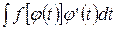 ;
;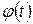 на х.
на х.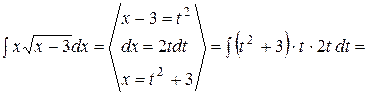
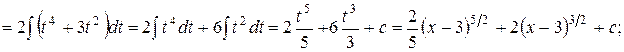
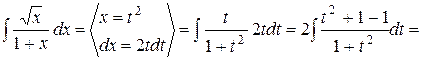
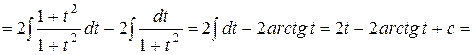
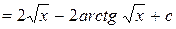 .
.


